Vicino Oriente antico. La matematica
Vicino Oriente antico. La matematica
La matematica
Gli esercizi metro-matematici nel III millennio
La ricerca sulla matematica mesopotamica conobbe il suo periodo pionieristico a partire dalla seconda metà dell'Ottocento, quando cominciarono a essere comprese la metrologia e le notazioni numeriche usate nei testi amministrativi cuneiformi. Tra il 1916 e il 1945 si ebbe un rapido aumento di testi matematici cuneiformi provenienti dai musei del Vecchio e Nuovo Mondo, individuati e pubblicati (anche se, spesso ritrovati nel corso di scavi non autorizzati, non avevano una provenienza nota), dei quali cominciò a essere compresa la difficile e particolare terminologia. A partire dagli anni Settanta del Novecento si è avuta una ripresa di questi studi, che si sono allargati ai testi cuneiformi matematici e metro-matematici del III millennio, ai documenti del IV millennio ‒ anteriori, quindi, all'avvento della scrittura ‒ e a numerosi nuovi testi matematici tardobabilonesi, così come a quelli cuneiformi provenienti da regioni periferiche. Sono state rimesse in questione traduzioni e interpretazioni consolidate dei testi già pubblicati, e sono apparsi i primi studi generali sull'intero corpus dei testi matematici mesopotamici. Poiché sono continuamente portati alla luce nuovi testi che, nella maggior parte dei casi, contengono sorprese sotto forma di nuovi tipi di problemi, gli studi futuri potranno modificare e precisare la nostra comprensione della vera estensione della matematica mesopotamica, in particolare di quella tardobabilonese e di quella precedente al periodo paleobabilonese.
I vari sistemi per denotare i numeri, sia nella scrittura protocuneiforme che vide la luce in Mesopotamia (3300 ca.) sia nella scrittura protoelamica della Persia antica, si possono interpretare come una continuazione diretta di sistemi simili di contrassegni di argilla, precedenti la scrittura, diffusi (con poche varianti) nella Persia antica, in Mesopotamia e in Siria (v. cap. VI, par. 1). La complessità della famiglia protocuneiforme di sistemi numerici, e la relativa complessità di numerosi tipi di testi amministrativi risalenti al periodo dei primi documenti scritti, rendono evidente che già 5200 anni fa l'insegnamento della numerazione deve aver svolto un ruolo importante nelle scuole scribali mesopotamiche. Come mostrano i testi che ci sono pervenuti, il curriculum scolastico degli scribi nel primo periodo della scrittura doveva comprendere gli elementi fondamentali dell'aritmetica, semplici calcoli di aree, divisioni e la risoluzione di alcuni sistemi di equazioni lineari. È questo l'inizio della tradizione matematica in Mesopotamia.
I testi matematici cuneiformi o protocuneiformi in nostro possesso del periodo prebabilonese in Mesopotamia (3200-2000 ca.) possono essere classificati come 'esercizi metro-matematici', in quanto sono esercizi scolastici nei quali si tratta soprattutto di notazioni per misure e di calcoli relativi a misurazioni. I più antichi, risalenti al periodo degli esordi della scrittura, trattano di distribuzione di terre ('testi di campi') o di cibo ('testi di razioni'). Spesso, ciò che distingue un esercizio metro-matematico da un testo amministrativo (relativamente complicato) è soltanto il fatto che il primo prende in considerazione numeri 'interessanti' (numeri esageratamente grandi o piccoli, cifre tonde o quasi, numeri 'irregolari' ‒ cioè non contenenti i fattori primi di 60 ‒, come 7, 11 e 13, e così via), oppure è privo di qualsiasi riferimento a date, nomi, titoli, che sono, viceversa, necessari per rendere significativo un testo amministrativo. L'aspetto notevole consiste nel fatto che alcuni dei tratti più caratteristici e (per noi) curiosi della matematica babilonese possono essere rintracciati fin dall'introduzione della scrittura (v. cap. VI, par. 3). In particolare, nell'imparare come predisporre in anticipo complicate distribuzioni di razioni per operai o di lotti di campi, gli allievi nella scuola scribale, ai primordi della scrittura, si trovavano ad affrontare vari tipi di intricati 'problemi di divisione', e dovevano saper operare con 'numeri quasi interi' del tipo [1+(1/n)], dove n è un numero intero piccolo.
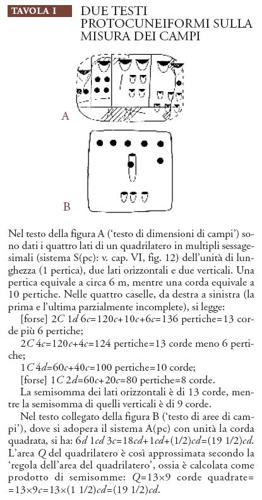
Molti esempi di testi risalenti ai più antichi 'stadi di scrittura' in Mesopotamia (Uruk e Susa, 3200 ca.) si occupano di misure lineari di campi ('testi delle dimensioni dei campi') e altri di misure di area di essi ('testi delle aree dei campi'): i primi sono probabilmente esercizi metro-matematici assegnati ad allievi e i secondi le soluzioni. A titolo di esempio, nella Tav. I sono messi a confronto due testi di questo genere, relativi a un terreno a forma di quadrilatero.
Questo e altri esempi suggeriscono l'ipotesi che l'insegnante scegliesse le dimensioni in modo che la misura del campo assegnato fosse vicina a una cifra tonda (in questo caso 20cd), e che il rapporto delle semisomme dei due lati orizzontali e di quelli verticali fosse vicino a un rapporto interessante (3/2). A questo scopo potrebbe essere stato utilizzato l'intelligente procedimento dell''estensione del campo' (Tav. II), il quale, fra l'altro, mostra molto chiaramente che le radici della matematica paleobabilonese risalgono ai primi stadi della scrittura; in particolare, si registra una stretta affinità con l''algebra metrica' paleobabilonese (v. oltre).
Un'altra categoria di testi metro-matematici del primo periodo della scrittura è data da un numeroso gruppo di 'testi di ripartizione di campi', nei quali si richiede di suddividere grandi appezzamenti di terreno tra cinque alti funzionari (secondo regole non molto chiare). A un certo punto del procedimento di divisione occorre determinare, dati l'area e un lato, l'altro lato di un rettangolo. Problemi di 'divisione metrica' di questo genere compaiono regolarmente nella geometria mesopotamica e nell'algebra metrica più tarda.
I testi metro-matematici paleosumerici
I pochi testi matematici del periodo paleosumerico (2500-2300) che ci sono pervenuti comprendono tavole di quadrati, calcoli di aree ed esercizi sulla divisione, spesso con numeri molto grandi. Testi analoghi, su tavolette di argilla e nella scrittura cuneiforme sumerica, sono stati trovati nella città siriana di Ebla, in area semitico-occidentale. Si tratta del più antico esempio, tra i molti che abbiamo, che dimostra come l'uso della scrittura cuneiforme in regioni che si trovano alla periferia della Mesopotamia abbia portato con sé lo studio della matematica di tipo mesopotamico (fig. 1).
Un tipico esempio di esercizio metro-matematico, in quanto coinvolge numeri irrealisticamente grandi e non presenta le informazioni precise presenti nei testi amministrativi, è stato ritrovato nella città di Shuruppak: il problema (Tav. III) consiste nel calcolare il numero di razioni giornaliere d'orzo contenute in un granaio, mediante conteggi con numeri sessagesimali in notazione posizionale (Tav. IV).
Un esercizio simile, quasi altrettanto antico, proveniente da Ebla, rappresenta invece il più antico esempio conosciuto di testo matematico con una numerazione decimale. Sempre da Shuruppak proviene invece il più antico esempio finora conosciuto di testo metro-matematico presentato a forma di tavola: si tratta di una tavola del tipo 'lato e area del quadrato', che si riferisce ad aree di quadrati 'da grandi a medi', con lati che vanno da 10×60 pertiche a 5 pertiche. In un esercizio collegato appare l'area di un quadrato molto grande, di lato pari a 50×60 pertiche: è questo il più antico esempio conosciuto di un numero troppo grande per essere la misura di un terreno reale che compare in un testo matematico.
Negli esercizi metro-matematici i numeri possono essere anche 'irrealisticamente piccoli': un esempio è offerto da una tavola di quadrati, proveniente dalla città paleosumerica di Adab, che elenca 'aree di piccoli quadrati' con lati che variano da 1 a 11 cubiti (in Babilonia 12 cubiti equivalevano a una pertica e un cubito equivaleva a 0,495 m ca.). Le aree elencate sono espresse in termini di tipi differenti di 'piccole frazioni' dell'unità fondamentale di area: appare chiaro che parecchie di queste frazioni inserite nel sistema A di numeri per misurare aree (identico al precedente sistema protocuneiforme) erano prese in prestito da un altro sistema, il sistema paleosumerico per i pesi (dei metalli preziosi) M(ps), subentrato (forse) al sistema protocuneiforme E(pc) (v. cap. VI, par. 3). Questo nuovo sistema di notazioni per numeri indicanti misure di peso sembra esser derivato da una combinazione di due sistemi paralleli di numeri ponderali, cioè Mr(ps) per il rame e Ma(ps) per l'argento (fig. 1). Dal momento che l'argento era 180 volte più costoso del rame, l'unità ponderale ('mina di scambio') di argento (3 g ca.) era 180 volte più piccola di una normale 'mina' di rame (500 g ca.). Per la stessa ragione, la più piccola frazione nel sistema argenteo, il 'grano' o 'chicco d'orzo' (1/20 g ca.), era 180 volte più piccola della più piccola frazione nel sistema del rame, il siclo (8 1/3 g ca.).
Infine, il più antico disegno che serve a illustrare un problema geometrico proviene ancora dalla città di Shuruppak. Anche se molto elementare, è importante perché si tratta del più antico documento nel quale il cerchio è considerato un oggetto matematico. In esso è rappresentato un quadrato che circoscrive quattro cerchi molto vicini, costituendo un antecedente di un problema tipo, noto attraverso una famosa tavoletta paleobabilonese, che conteneva originariamente più di quaranta esercizi, dove alcuni quadrati di lato 60 pertiche sono divisi in vari modi in parti più piccole delimitate da linee rette e archi di circonferenza, e dove l'obiettivo è quello di identificare le parti con il loro nome e trovarne l'area (v. oltre). Nella tavoletta paleosumerica i quattro cerchi inscritti circondano un 'quadrato concavo' formato da quattro quarti di cerchio. Quadrati concavi e 'triangoli concavi' formati allo stesso modo appaiono come 'finestre a forma di lira' in testi di problemi e in tavole di costanti paleobabilonesi.
Problemi di rettangoli e trapezi in testi paleoaccadici
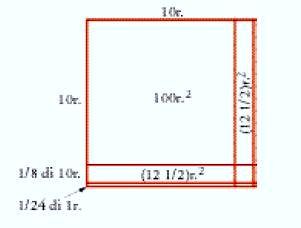
Un ristretto numero di brevi testi metro-matematici dell'epoca dei sovrani paleoaccadici della dinastia sargonica (2300 ca.) riportano uno o più problemi di 'geometria numerica', con o senza soluzione. In tutti i casi, eccetto uno, il problema è formulato in termini di lati e aree di rettangoli o quadrati: si tratta di problemi apparentemente semplici, ma in realtà piuttosto sofisticati. Uno di questi testi pone il problema di come trovare il lato minore di un rettangolo quando l'area è di 100 pertiche quadrate e il suo lato maggiore è di 243 pertiche. Queste due misure sono espresse in numeri sessagesimali 'regolari' (infatti 243 è come dire 240, cioè 4 volte 60, più 3, il quale ultimo è 1/20 di 60), che sembrano scelti appositamente affinché il problema di divisione enunciato abbia una 'soluzione esatta' in termini delle unità di misura della lunghezza dell'epoca (v. oltre). Analogamente, in un problema relativo al calcolo del lato e dell'area di un quadrato, la lunghezza del lato era stata probabilmente scelta appositamente della forma 10 pertiche +1/8 di 10 pertiche +1/24 di pertica (fig. 5: r., dall'ingl. rod, sta per 'pertica'). La lunghezza 10 pertiche +1/8 di 10 pertiche può essere stata ottenuta utilizzando una variante del procedimento dell'estensione di un terreno (v. sopra) come un'approssimazione del lato di un quadrato nel caso in cui si richieda che l'area sia uguale alla cifra tonda di 125 pertiche quadrate. Il calcolo dell'area del quadrato nel problema assegnato era probabilmente accompagnato da un riferimento più o meno esplicito a una figura geometrica.
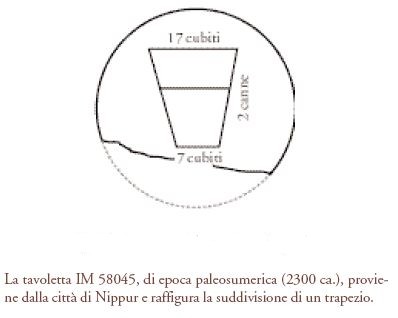
Oltre ai testi paleoaccadici di problemi riguardanti rettangoli o quadrati, si conosce un solo testo con un problema che si può quasi definire di teoria dei numeri e che è relativo a suddivisioni di un trapezio. Una piccola tavoletta contiene il disegno di un trapezio diviso in due parti da una linea trasversale (fig. 6). Le lunghezze dei due lati paralleli alla trasversale sono date come 7 e 17 cubiti, rispettivamente, mentre l'altezza è uguale a 2 canne (12 cubiti). Il compito assegnato è quello di trovare la lunghezza della trasversale che divide il trapezio in due parti di area eguale ('trapezio equidecomposto'). Questo testo, che illustra bene la sorprendente raffinatezza della matematica paleoaccadica, è il più antico esempio conosciuto di quella che sarebbe divenuta una delle più impressionanti conquiste della matematica paleobabilonese: lo studio dei 'trapezi equipartiti'. Se un trapezio con due lati paralleli m e n è diviso da una terza parallela d in due sottotrapezi di aree eguali, allora (m, d, n) è la soluzione dell'equazione quadratica indeterminata □[≡area del quadrato di lato]m+□n=2□d, come dire, in termini moderni, m2+n2=2d2 (un caso speciale dell'equazione di partizione di un trapezio). La soluzione (m=17; d=13; n=7) dell'esempio è una soluzione in numeri interi particolarmente semplice di questa equazione, dalla quale consegue che la trasversale suddivide l'altezza secondo il rapporto 2:3.
Il periodo neosumerico
Lo Stato centralizzato della III dinastia di Ur (2000 ca.), ancor più di quello precedente del periodo paleoaccadico, fu caratterizzato da una burocrazia enormemente sviluppata che teneva registrazioni estremamente elaborate di numerosi tipi di transazioni; tuttavia, abbastanza stranamente, nessun testo matematico (né, del resto, altri tipi di testi scolastici) è stato finora ritrovato fra gli innumerevoli testi amministrativi conosciuti di questo periodo. L'unica eccezione notevole è una tavoletta cuneiforme contenente un calcolo che riguarda la crescita regolare, anno per anno, del numero dei capi di bestiame di un armento per un periodo di 10 anni, in determinate condizioni. Si tratta di un complesso esercizio metro-matematico di tipo algoritmico e, in quanto tale, rappresenta un precedente dell'algoritmo aritmetico paleobabilonese per il raddoppiamento di un dato numero sessagesimale regolare in 10 o 30 passi, così come delle tavole di potenze paleobabilonesi (che arrivano sempre alla decima potenza) e persino di esercizi tardobabilonesi che richiedono la somma dei primi 10 termini di una successione di quadrati o di potenze di 2. Discende da questo 'algoritmo di crescita' anche un testo paleobabilonese proveniente dall'avamposto settentrionale di Mari, riguardante il risultato che si ottiene raddoppiando ogni giorno, per 30 giorni di seguito, il peso iniziale di un chicco d'orzo (non si può non pensare alla leggenda indiana sul premio promesso all'inventore del gioco degli scacchi, e al famoso 'problema dei conigli' di Leonardo Pisano).
Non si conoscono testi di contenuto geometrico di questo periodo, ma è quasi certo che i programmi scolastici contenevano una notevole quantità di 'matematica pratica', comprese applicazioni di geometria piana e solida. Molti testi di carattere amministrativo, alcuni anche del precedente periodo paleoaccadico, contengono calcoli molto precisi di volumi di oggetti più o meno complicati (per es., muri di mattoni) o di scavi (il più delle volte canali). Un ruolo importante in calcoli di questo tipo era svolto dal contare con mattoni di diverse forme standard, utilizzando particolari 'numeri di mattoni'.
La matematica babilonese
Due fattori sembrano aver favorito uno sviluppo sorprendentemente rapido della matematica all'inizio del periodo paleobabilonese (1900-1600). Innanzitutto l'invenzione di un sistema di 'notazione posizionale' per il sistema di numerazione sessagesimale (Tav. IV), nel quale uno stesso simbolo ha diverso valore se scritto prima di altri, avvenuta probabilmente intorno al 2000, cioè proprio prima dell'inizio del periodo paleobabilonese. Importante fu anche un mutamento nel clima culturale, cioè il passaggio da uno Stato centralizzato e da una burocrazia onnipresente e presumibilmente caratterizzata, per quanto attiene all'insegnamento delle tecniche di calcolo, da un approccio meramente utilitaristico, a una burocrazia meno onnipresente e più aperta alle istanze individuali.
L'invenzione del sistema di notazione posizionale per i numeri sessagesimali fu in parte una conseguenza del fatto che, almeno fin dall'introduzione della scrittura, per caso o volutamente, nei segni adoperati per gli elementi nel sistema sessagesimale S di numeri per contare (v. cap. VI, par. 3) il segno cuneiforme per il 60 era della stessa forma del segno cuneiforme per l'1, però più grande, mentre gli elementi intermedi del sistema (multipli con un fattore 10) si ottenevano con un'unica procedura grafica. È probabile, però, che essa fosse anche in parte ispirata dal precedente uso (implicito) della notazione posizionale per i numeri rappresentati dai contrassegni su una tavoletta di calcolo o abaco. Non vi è alcuna evidenza archeologica diretta a sostegno dell'ipotesi che gli scribi mesopotamici utilizzassero abachi o strumenti simili allo scopo di facilitare i calcoli, tuttavia le prove indirette sono piuttosto consistenti. Oltre alle testimonianze linguistiche (parole che sembrano alludere a tavole di calcolo e ad operazioni con contrassegni), bisogna considerare che i risultati delle addizioni o delle moltiplicazioni, anche le più complicate, erano sempre scritti direttamente, senza indicazione di come fossero stati ottenuti. Inoltre, nei testi matematici paleobabilonesi i numeri sessagesimali in notazione posizionale erano utilizzati principalmente per appuntare i risultati intermedi dei calcoli, come se si copiasse una successione di numeri ricavata con l'ausilio di una tavola di calcolo. Negli enunciati dei problemi, tuttavia, e nelle 'risposte', spesso i numeri erano scritti con le tradizionali notazioni relative ai numeri utilizzati per contare (sessagesimali o decimali), oppure ai numeri che esprimono misure di capacità, di peso, di superficie, e così via.
I problemi pratici che si trovano nei testi matematici paleobabilonesi riguardano oggetti e operazioni di carattere quotidiano, come mattoni, contenitori, fasci di canne e di tronchi, scavo e manutenzione di canali, sterri, rampe e fortificazioni, muri e argini, prezzi di mercato, eredità e divisioni di proprietà, tassi di interesse, pecore e lana, attrezzi agricoli, bitume, intonaco e così via, forse anche orologi ad acqua. È interessante notare che tutti i problemi pratici di questo tipo devono essere stati studiati anche nelle scuole scribali neosumeriche, sebbene non sopravviva alcun documento che possa provare questa affermazione. Molto spesso tali problemi pratici erano un pretesto per esercitarsi con tecniche matematiche elementari e generali, come fare uso di costanti, calcolare volumi, applicare la regola del tre o la regola di falsa posizione, calcolare con progressioni aritmetiche o geometriche o trovare le medie aritmetiche o armoniche.
Più precisamente, nei testi matematici babilonesi non erano prese in considerazione le medie armoniche come tali, bensì due concetti molto interessanti correlati ad esse, ossia i 'tassi combinati di produzione' e i 'prezzi combinati di mercato'. I 'tassi di produzione' w relativi a un dato tipo di lavoro erano espressi in termini di quantità di prodotto risultante da una giornata di lavoro degli operai e i tassi combinati di produzione relativi ai vari tipi lavoro erano calcolati mediante formule del tipo 1/[(1/w1)+(1/w2)+…] oppure 3/[(1/w1)+(1/w2)+…], a seconda delle circostanze. Per esempio, in un testo si trova che a tassi di produzione relativi al lavoro per frantumare, modellare e mescolare l'argilla, pari rispettivamente a 20, 20 e 10 sicli di volume a giornata di lavoro, corrisponde un tasso combinato di produzione di mattoni pari a 5 sicli di volume a giornata di lavoro; infatti il calcolo dà: 1/[(1/20)+(1/20)+(1/10)]=1/(;03+;03+;06)= =1/;12=5, dove per le frazioni unitarie si è usata la notazione, caratteristica di quella matematica, 1/n=;m, essendo m=60/n. Lo stesso avveniva per i prezzi di mercato m, i quali erano espressi in termini di unità di alcune merci/sicli d'argento.
I testi matematici contenenti problemi geometrici si occupavano proprio di ciò che la parola greca 'geometria' suggerisce, ossia la misurazione del terreno; infatti, lo scopo della geometria paleobabilonese (a differenza della successiva geometria greca) era di presentare metodi per calcolare le aree o i lati di campi. Nella maggior parte dei casi, le aree erano di grandezza reale; il rettangolo normale aveva i lati di 30 e 20 pertiche (ca. 180 e 120 m). I metodi usati si basavano su formule per calcolare le aree (errate nel caso di un quadrilatero qualsivoglia), sulla regola del triangolo rettangolo (1500 anni prima di Pitagora), su regole di similitudine e sulla suddivisione delle figure. Il valore usato per π era (per convenienza o per tradizione) semplicemente 3. Per i volumi, l'area della base era misurata in pertiche quadrate, mentre le altezze erano misurate in cubiti, probabilmente allo scopo di evitare calcoli con piccole frazioni. I volumi di oggetti semplici erano calcolati correttamente, mentre in casi più difficili i volumi erano calcolati talora correttamente, talora no. Raramente si trovano nei testi disegni di oggetti tridimensionali e, quando sono presenti, essi sono sempre difficili da interpretare, poiché mancano di prospettiva (sulla geometria babilonese, v. la successiva Tav. VIIa, VIIb, VIIc).
Tavole matematiche, tavole metrologiche e tavole di costanti
L'inizio dell'uso del sistema di notazione posizionale per i numeri sessagesimali è strettamente legato alla compilazione delle prime tavole cuneiformi matematiche e metrologiche, le quali a loro volta si rivelarono uno strumento di fondamentale importanza per risolvere problemi relativi alla misurazione, facilitando i calcoli relativi.
I tipi più comuni di tavole matematiche sono le tavole di moltiplicazione, le tavole di quadrati o di radici quadrate e le tavole di reciproci o inversi. In queste tavole si trovano soltanto numeri sessagesimali, scritti in notazione posizionale. Le tavole metrologiche, invece, elencano le notazioni tradizionali, in ordine crescente, per un assortimento scelto di numeri che rappresentano misure appartenenti a uno dei sistemi C (capacità), M (metallo), A (area) e L (lunghezza): per ognuna delle misure selezionate la tavola metrologica indica anche il suo valore come multiplo sessagesimale di una certa unità di base (non menzionata esplicitamente). Un quadro delle principali unità di misura in uso nella Mesopotamia è stato fornito con la Tav. III (a, b) del precedente cap. VI.
Nessuna tavola metrologica sumerica è stata ancora trovata, e nemmeno sono state ancora trovate tavole di moltiplicazione sumeriche. Se fosse vero che gli scribi e i contabili neosumerici non disponevano di tavole metrologiche, ciò avrebbe costituito un grosso svantaggio. Sono documentate, invece, alcune tavole di reciproci che sembrano risalire al periodo neosumerico. Questa circostanza è particolarmente interessante poiché una delle caratteristiche peculiari della matematica 'babilonese' consiste proprio nel modo in cui sono trattati i reciproci dei numeri sessagesimali. Nell'educazione matematica paleosumerica la divisione per numeri 'notevoli' come 7 e 11, cioè la divisione con un resto, sembra fosse un esercizio molto apprezzato. Nella matematica paleoaccadica, non molto più tardi, l'attenzione sembra essersi spostata sulla divisione per numeri sessagesimali regolari, allo scopo di ottenere risultati esatti, senza resti. Un numero sessagesimale 'regolare' può essere definito (in termini moderni) come un numero n (intero) per il quale esista un numero reciproco n′ (anch'esso intero), tale che il prodotto n×n′ sia uguale a qualche potenza (positiva) di 60. Per esempio, se (in notazione sessagesimale posizionale) n=4.03 (=4×601+ 3×600=243)=3×3×3×3×3, allora n′=20×20×20×20×20= =14.48.53.20 (=3.200.000), e n×n′=60×60×60×60×60. Condizione necessaria e sufficiente perché n sia regolare è che contenga soltanto gli stessi tipi di fattori primi di 60, cioè 2, 3 o 5. Ora, se n è un numero regolare e n′ il suo reciproco, allora il numero 1/n è n′ moltiplicato per qualche potenza di 1/60. Nel sistema di notazione posizionale babilonese, dove tutte le potenze di 60 sono scritte come '1' (non esiste un segno per indicare lo zero), la frazione 1/n è quindi formalmente eguale a n′. Anziché parlare di 'tavole di reciproci' cuneiformi, sarebbe pertanto più corretto parlare di tavole di frazioni cuneiformi, dove le frazioni del tipo 1/n, con n regolare sessagesimale compreso fra 3 e 1.21 (=1×601+21×600=81= =3×3×3×3), sono espresse come frazioni sessagesimali nel sistema di notazione posizionale.
Con l'avvento delle tavole matematiche e metrologiche, divennero banali problemi tipici come trovare l'area di un rettangolo (o di un quadrato) di lati noti, trovare il lato di un quadrato di area nota, trovare il secondo lato di un rettangolo di area e primo lato noti, già familiari, insieme a modi efficaci di risolverli, agli scribi fin dai primordi della scrittura e per tutto il III millennio. Per risolvere facilmente tali problemi bastava utilizzare appropriate tavole metrologiche, per passare da numeri di lunghezza o di area a numeri sessagesimali e viceversa, e una tavola di moltiplicazione, una tavola di radici quadrate o una tavola di reciproci, per effettuare i necessari calcoli con i numeri sessagesimali. Sembra plausibile supporre che, così come il fattore che consolidò l'invenzione della scrittura fu la compilazione di un certo numero di testi lessicali con lunghe liste di segni (proto)cuneiformi ordinati per soggetto (v. cap. VI, par. 2), allo stesso modo ciò che segnò l'inizio della matematica babilonese fu la compilazione di questi due tipi di testi cuneiformi disposti come tavole: da una parte le tavole matematiche combinate, contenenti una tavola di reciproci, una serie di tavole di moltiplicazione per piccoli numeri sessagesimali regolari e i loro reciproci e una tavola dei quadrati, e, dall'altra parte, le tavole metrologiche, con sottotavole per i vari sistemi numerici.
Infine, sono state trovate anche alcune tavole di costanti, dieci di esse paleobabilonesi e due (forse) tardobabilonesi, benché non vi sia nessun indizio che sia mai esistita una tavola di costanti cuneiforme standard. Una tavola paleobabilonese ritrovata a Susa menziona 70 costanti di ogni tipo, incluse costanti per figure geometriche delimitate da linee rette o archi di circonferenza, costanti associate a volumi o a lavori di costruzione e costanti per materiali. Le costanti geometriche più citate nei testi sono l'area, e, in alcuni casi, il diametro e la diagonale di certe figure geometriche specificate e caratterizzate da un arco o da una linea di lunghezza unitaria che le delimita. È inteso, naturalmente, che in generale i diametri sono proporzionali alla lunghezza dell'arco o della linea che delimita la figura e che l'area è proporzionale al quadrato di questa lunghezza. Gli enti geometrici che appaiono nelle tavole delle costanti e nei testi dei problemi sono cerchi, semicerchi, figure a forma di barca o di chicco, quadrati o triangoli concavi, quadrati, rettangoli e, in generale, quadrilateri, triangoli rettangoli o equilateri, trapezi e poligoni regolari con 5, 6 o 7 lati (v. oltre).
In aggiunta alle costanti geometriche, nelle varie tavole sono menzionate spesso costanti per mattoni ('numeri di mattoni'), per recipienti ('numeri di stoccaggio') e costanti che riguardano tassi standard per un determinato tipo di lavoro o di operazione ('numeri di trasporto', 'numeri per i percorsi', e così via). Queste costanti svolgono un ruolo importante nei corrispondenti esercizi metro-matematici, vale a dire nei testi di problemi geometrici o pratici. È probabile che le tavole di costanti siano state compilate come collezioni di costanti tratte da testi di problemi: di conseguenza, la presenza nelle tavole di numerose costanti di cui non possediamo nessuna interpretazione indica che vi sono numerose categorie di testi cuneiformi di problemi matematici che finora non sono state portate alla luce.
Gli algoritmi
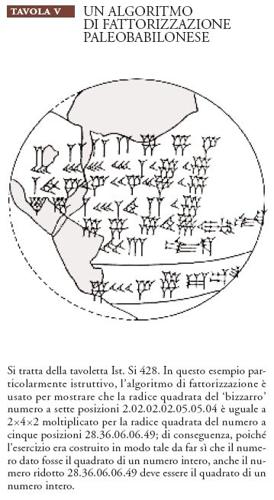
Le tavole matematiche di radici quadrate o radici cubiche, di cui si conoscono vari esempi, non sono molto complete e non devono essere state molto utili nella pratica. Per trovare radici quadrate o cubiche laddove le tavole non erano sufficienti si disponeva di due algoritmi differenti ma complementari: il primo di questi era un algoritmo di fattorizzazione (Tav. V), basato sull'idea che se un 'intero' sessagesimale a contiene un fattore quadrato □n, allora la radice quadrata di a contiene il fattore n. Nei casi in cui n è un numero sessagesimale piccolo e regolare, è facile trovare e togliere da a il corrispondente fattore quadrato □n. Il processo può essere continuato fino a che tutti questi fattori quadrati siano stati rimossi. Vi sono inoltre numerosi esempi, nel corpus di problemi paleobabilonesi, nei quali, nel mezzo di una procedura di risoluzione, è calcolata la radice quadrata di un numero sessagesimale a molte posizioni, senza che i dettagli del calcolo siano mai forniti. Tuttavia, in tutti questi casi, il numero dato è un quadrato esatto di un sessagesimale 'intero' e, quindi, ogni approssimazione sufficientemente buona della radice quadrata, produrrebbe immediatamente quell'intero. Nell'esempio della Tav. V la radice quadrata 5.20.53 di 28.36.06.06.49 probabilmente era ricavata in questo modo.
Per le radici quadrate di numeri non quadrati perfetti i matematici paleobabilonesi ottenevano approssimazioni del primo ordine mediante l'uso di un secondo algoritmo, basato sulla regola data dalla formula (□S+R)1/2=S+[R/(2S)], che si può dimostrare geometricamente (le argomentazioni avrebbero potuto essere comprese anche dai matematici del periodo paleoaccadico). Applicata una volta, questa regola di approssimazione permetteva di mostrare che la radice di 2 è uguale a circa 1;25 (vale a dire, 17/12), la radice di 3 è uguale a circa 1;45 (ossia 7/4), e così via. Applicata più volte, la regola può essere stata adoperata per mostrare che la radice di 2 è uguale a circa 1;24.51.10, un valore che è stato ritrovato in una rappresentazione geometrica e anche in una tavola di costanti.
Un ingegnoso algoritmo di duplicazione e divisione (a metà) veniva adoperato per produrre successioni di coppie di numeri sessagesimali regolari reciproci (n, n′). Per esempio, a partire da una coppia iniziale (2.05, 28.48; si osservi che 2.05=5×5×5 e 28.48=12×12×12), l'algoritmo produceva le coppie successive (4.10, 14.24), (8.20, 7.12), (16.40, 3.36), e così via. Altrettanto interessante è un algoritmo basato sull'idea di 'trascinare una parte' che è usato in un testo, ancora ben conservato, per verificare tali risultati. Per esempio, se si vuole verificare che la coppia (2.13.20, 27) è corretta, per applicare questo algoritmo si comincia con l'osservare che 20 (=20/60, ossia il reciproco di 3) è un fattore di 2.13.20, e che infatti 2.13.20=3′×6.40 (vale a dire, nella moderna notazione numerica, 8000=20×400, indicandosi con 3′ il numero 60/3); nel passaggio successivo un'ulteriore applicazione dell'algoritmo mostra che 3′×6.40=3′×3′×20=9′×20; nel passaggio finale si ottiene 9′×3′×1=27′, il che conferma che 2.13.20′=27.
Infine, un ben noto esempio di algoritmo paleobabilonese, geometrico piuttosto che aritmetico, è offerto da un testo accompagnato da un'illustrazione, nel quale si mostra in che modo una progressione geometrica decrescente di triangoli rettangoli simili può essere costruita disegnando le altezze sulle ipotenuse dei triangoli rettangoli, sempre più piccoli, che appaiono in successione (fig. 11).
Equazioni e sistemi di equazioni a una o più variabili: l'algebra metrica
Vari metodi per risolvere equazioni o sistemi lineari erano noti nel periodo paleobabilonese, come dimostrano alcuni, non troppo numerosi, testi conservati su problemi che coinvolgono le questioni alle quali facciamo riferimento modernamente con questi termini. Tuttavia, a quanto pare, il caso generale di tre o più equazioni non omogenee era ancora al di fuori della portata delle tecniche matematiche dell'epoca. Le equazioni lineari a una incognita erano di solito di una complessità voluta. Il caso è bene illustrato da un piccolo frammento proveniente da Babilonia, in cui il problema enunciato era quello di trovare la quantità di orzo contenuta inizialmente in un deposito, posto che ne fossero rimasti 5×60 sìla, dopo che in cinque momenti successivi fossero state prelevate varie frazioni dell'ammontare residuo di orzo. Nella notazione moderna, il problema può essere formulato come un'equazione: C[1−(1/5)][1−(1/3)][1−(2/5)][1−(1/2)][1−(3/5)]=5×60. Il problema era risolto utilizzando la regola della falsa posizione; è molto probabile che questo particolare tipo di problema, e la sua risoluzione, avesse radici molto antiche.
I sistemi di due equazioni lineari a due incognite erano risolti facilmente utilizzando ancora la regola della falsa posizione, purché una delle equazioni fosse omogenea, cioè priva del termine costante. Il caso più difficile di due equazioni non omogenee è illustrato da un esempio ben noto, riguardante il rendimento di due campi.
I sistemi di equazioni rettangolari-lineari e quadratico-lineari (e le connesse equazioni quadratiche) avevano un ruolo rilevante nella matematica paleobabilonese. Le due varianti fondamentali di 'sistemi rettangolari-lineari' a due incognite u e s corrispondevano alle due coppie di equazioni us=A e u±s=m. Analogamente, le quattro varianti fondamentali di 'sistemi quadratico-lineari' corrispondevano alle quattro coppie di equazioni □m±□n=S e m±n=p.
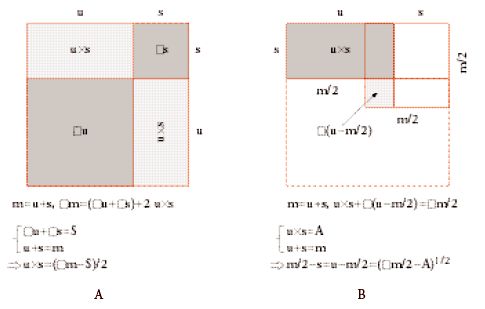
A lungo è stato ritenuto dagli storici della matematica babilonese che le procedure di risoluzione per tali sistemi di equazioni fossero basate su identità algebriche del tipo della regola quadratica del mezzo termine, cioè □[(u+s)/2]−□[(u−s)/2]=us, e della regola dei coniugati, cioè (m+n)(m−n)=□m−□n.
Recentemente è stato dimostrato invece che molte particolarità proprie della terminologia matematica nei testi di problemi paleobabilonesi possono essere spiegate solo postulando che le procedure di risoluzione per i sistemi di equazioni rettangolari-lineari e quadratico-lineari fossero basati su una 'geometria ingenua' (Høyrup 1990). Così, per esempio, una frase come 'moltiplica a per b' non è espressa nello stesso modo quando a è un fattore numerico e b una lunghezza, rispetto a quando a e b sono invece entrambe lunghezze. Inoltre, mentre sumerogrammi di vario genere sono molto frequenti nella maggior parte dei problemi paleobabilonesi, essi sono, invece, rari in testi che trattano di sistemi di equazioni rettangolari-lineari o quadratico-lineari. La conclusione più ovvia è che lo studio di questi sistemi è da considerare un'autentica innovazione paleobabilonese, mentre gran parte del resto della matematica paleobabilonese può essere stata soltanto una continuazione e un'elaborazione di una tradizione risalente al III millennio.
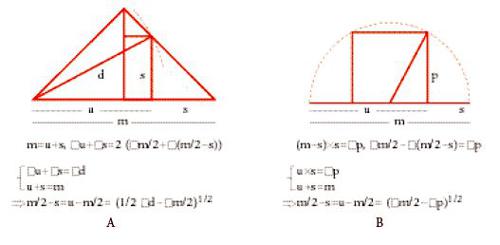
L'equivalente paleobabilonese della regola quadratica del mezzo termine era un'argomentazione numerico-geometrica di 'completamento del quadrato', così come l'equivalente della regola dei coniugati era probabilmente un'argomentazione numerico-geometrica relativa alla 'banda quadrata' (una banda quadrata è delimitata su due lati da due quadrati concentrici e paralleli). Molti dei più spettacolari risultati della matematica paleobabilonese erano ottenuti mediante questo tipo di metodi di natura numerico-geometrica, che è appropriato designare con il termine di 'algebra metrica'. Così, per esempio, è probabile che la regola per costruire soluzioni razionali all'equazione indeterminata di partizione di un trapezio □m+□n=2□d (v. sopra) sia stata ottenuta scegliendo come parametri arbitrari le altezze parziali di un trapezio equipartito. Analogamente, la regola per generare soluzioni razionali all''equazione indeterminata del triangolo rettangolo' □u+□s=□d è stata ottenuta probabilmente scegliendo come parametri arbitrari le lunghezze parziali del diametro di un semicerchio di centro c, quando il raggio r e l'altezza p opposta al diametro sono due lati del triangolo rettangolo (fig. 12A). Infine, la 'regola di composizione' □(ma+nb)+□(mb−na)=(□m+□n)(□a+□b), usata per costruire soluzioni 'confluenti' per l'equazione di partizione di un trapezio, può essere stata ottenuta lavorando con le sezioni di un 'birettangolo' formato congiungendo due triangoli rettangoli lungo una diagonale comune (fig. 12B); e così via.
La matematica tardobabilonese
Nel millennio successivo al periodo paleobabilonese la Bassa Mesopotamia subì un'oppressiva dominazione straniera e, per questo lungo intervallo, non vi sono pressoché tracce di attività matematica. Tuttavia, intorno alla metà del I millennio, la situazione politica e culturale migliorò. A partire da quest'epoca e lungo tutto il periodo seleucide (dopo la conquista greca) vi fu una nuova fioritura della matematica, anche se sono stati ritrovati pochi testi di problemi risalenti a quel periodo. È interessante notare una fondamentale differenza nella terminologia, segno di quanto la matematica tardobabilonese si fosse allontanata dalla precedente matematica paleobabilonese, sebbene, allo stesso tempo, molti dei tratti caratteristici della matematica paleobabilonese possano essere ancora osservati nei testi di problemi tardobabilonesi. Sembra che l'interesse per le tavole matematiche ampie e complicate sia aumentato, come conseguenza naturale dello sviluppo dell'astronomia tardobabilonese (v. cap. XII). Particolarmente impressionanti sono i diversi esempi di tavole tardobabilonesi di reciproci, di quadrati e perfino di quadrati di quadrati di quasi tutti i numeri sessagesimali regolari 'a sei posizioni'. Un'innovazione degna di nota consiste nel fatto che in alcuni testi di problemi tardobabilonesi le procedure di risoluzione numerica sono precedute di solito da una regola di calcolo non numerico. Un'altra innovazione consiste nel fatto che la misura della superficie è normalmente espressa in termini di una misura di base, come nella società contemporanea, ed è quindi abbandonato il sistema tradizionale di misura delle aree. Di conseguenza, la natura metrico-algebrica della trattazione dei sistemi di equazioni rettangolari-lineari e quadratico-lineari diventa ancora più evidente che nei testi matematici paleobabilonesi.
L'alba della geometria
La geometria come noi la conosciamo ha avuto origine in Mesopotamia, sviluppandosi gradualmente nel corso di tre millenni e più. Un'affermazione così decisa deve però essere sostenuta da un'analisi più precisa di quali risultati siano dovuti ai 'geometri' della Mesopotamia (che erano poi scribi o insegnanti), a quali concetti geometrici abbiano dato vita e in che senso ciò che facevano merita di essere chiamato geometria. A quanto sembra, i primi oggetti geometrici, già nel periodo degli esordi della scrittura o anche prima, furono campi di forma rettangolare o quasi, la cui superficie era misurata in termini di unità d'area. L'idea di misura dell'area nacque in modo naturale in una società agricola come era quella della Mesopotamia: si trattava di una grandezza che poteva essere calcolata come la lunghezza del solco prodotto dall'aratro moltiplicata per il numero dei solchi e per la distanza costante tra i solchi. È significativo il fatto che ancora nel periodo paleobabilonese, molto più tardo, nei testi matematici i rettangoli misuravano di solito 30 corde per 20 corde, cioè la grandezza di un campo il cui prodotto era sufficiente a nutrire una famiglia.
Mezzo millennio più tardi il quadrato fece il suo ingresso nei testi matematici paleosumerici. L'idea di quadrato può essere di origine metrologica, perché le unità di misura più piccole per le aree nel sistema sumerico (ereditato dal periodo protocuneiforme) erano le unità di 'giardino', l'area di un quadrato di lato 1 pertica, e l'unità di 'diga (di terra)', l'area di un quadrato di lato 1 corda. Nel periodo paleosumerico compaiono anche per la prima volta i cerchi, in un disegno su una tavoletta d'argilla che mostra quattro cerchi inscritti in un quadrato. L'idea di cerchio doveva nascere naturalmente come immagine della Luna, o del Sole, o come il segno numerico D (v. cap. VI, fig. 10).
L'idea di calcolare il volume di un prisma a sezione rettangolare, un muro o un canale per esempio, moltiplicando l'area di base (data in pertiche quadrate) per l'altezza (in cubiti) deve essere molto antica, anche se i più antichi calcoli di volumi conosciuti si trovano in documenti amministrativi del periodo paleoaccadico. Anche l'idea analoga di calcolare il volume di un prisma a sezione trapezoidale moltiplicando l'area della sezione per la lunghezza deve risalire a periodi molto antichi, così come la misura della capacità di un recipiente cilindrico, la quale però doveva risultare tecnicamente più complicata, date le piccole misure che vi intervengono. La circonferenza e l'altezza del recipiente erano misurate in cubiti o dita (1 cubito equivale a 30 dita), e si moltiplicava poi il volume del recipiente per una costante, il 'numero di stoccaggio'.
Doveva poi essere noto da molto tempo che l'area del triangolo è la metà dell'area del rettangolo avente la stessa base e la stessa altezza; non abbiamo però testi che ci permettano di verificare questa ipotesi. Sono state inoltre trovate un paio di tavolette neosumeriche con mappe di campi, nelle quali un campo di forma irregolare è suddiviso in settori rettangolari, trapezoidali e triangolari, e l'area totale è determinata come somma delle aree di questi. La tavoletta paleoaccadica che riporta il disegno di un trapezio equidecomposto (v. sopra) è notevole non soltanto perché si tratta del più antico testo che riguarda trapezi decomposti, ma anche perché è il più antico testo matematico in cui è considerata una figura troppo piccola per rappresentare un vero campo coltivato: si tratta infatti di un trapezio di area uguale a 1 pertica quadrata.
Nella geometria paleobabilonese si ritrovano anche figure piane diverse dai soliti rettangoli, quadrati, trapezi, triangoli e cerchi, probabilmente viste come curiosità matematiche, forse ispirate alle decorazioni della ceramica e di altri oggetti. Ciò è chiaro nel caso dei poligoni regolari ('5 fronti', ecc.), dei quadrati concavi, dei triangoli, di tutte le figure concentriche e delle figure che contengono altre figure, e probabilmente anche per figure pseudorealistiche denotate con termini non matematici, come 'mezza luna', 'chicco', 'occhio di bue', 'arco' e 'città' (con quest'ultimo si indicavano i cerchi concentrici). È anche dubbio che dietro la suddivisione in strisce di triangoli o trapezi ci siano motivazioni concrete, come divisioni di proprietà terriere o sistemi di irrigazione. Per quanto riguarda i solidi diversi dai prismi e cilindri considerati nel periodo paleobabilonese, non è improbabile che l'idea di considerare tronchi di cono sia nata dalla necessità di calcolare il volume di un fascio di canne o di un ciocco di legno, e che quella di considerare le mura di una città (anelli conici) o rampe sia dovuta a necessità belliche. È anche possibile che il cono sia l'idealizzazione matematica di un mucchio di grano, e una piramide culminante in uno spigolo la forma di un magazzino per cereali. L'idea di piramide quadrata, infine, può essere stata importata dall'Egitto, dove aveva certamente avuto origine l'idea di piramide a gradini.
Nel seguito (Tav. VIIa, VIIb, VIIc) si presenta una rassegna dei principali tipi di figure piane o solide che costituiscono la parte essenziale della geometria mesopotamica, e si esaminano quali relazioni tra queste sono messe in evidenza e quali manipolazioni sono eseguite; in conclusione si considerano la natura e il grado di raffinatezza della geometria babilonese.
Le caratteristiche distintive della geometria babilonese
La geometria babilonese si è sviluppata in stretta relazione con la metrologia e con l'algebra metrica. Tutte le figure sono espresse in termini di lunghezze di lati, o di porzioni di lati, circonferenze, e così via, e/o in termini di aree, volumi, misure di capacità, e simili. Strettamente legati alle definizioni di area e di volume sono naturalmente i concetti di ortogonalità e di rette parallele, impliciti nella definizione di quadrati, rettangoli e angoli retti. La familiarità con il concetto di ortogonalità si può anche presumere nella considerazione di figure come cerchi, semicerchi e settori o doppi settori circolari (Tav. VII, figg. D-E), nelle quali il diametro e la linea trasversale sono ortogonali. Analogamente è evidente la familiarità con il concetto di rette parallele nel caso di triangoli o trapezi suddivisi in strisce (Tav. VII, fig. N); l'esempio più noto di linee ortogonali è il triangolo con una successione di altezze di triangoli rettangoli più piccoli (Tav. VII, fig. P3).
Il concetto generale di angolo era sconosciuto nella geometria babilonese, o comunque tenuto in scarsa considerazione, secondo quanto risulta dai documenti conosciuti. D'altra parte, almeno nel caso tridimensionale, la pendenza uniforme dei lati di un canale, di un muro o di una piramide era regolarmente espressa dalla variazione orizzontale corrispondente allo spostamento verticale di un'unità di lunghezza. Inoltre, anche in assenza di un concetto generale di angolo, il concetto di triangoli simili era ben chiaro ed era utilizzato in molte situazioni (Tav. VII, figg. P1-P2). È molto importante osservare che le tavole babilonesi di costanti per figure geometriche usano in modo essenziale i concetti gemelli di similitudine 'lineare' e 'quadratica', ossia il fatto che, in figure simili di qualunque tipo, lunghezze corrispondenti sono proporzionali e le aree sono proporzionali ai quadrati di queste lunghezze. Inoltre, in una società nella quale i mattoni costituivano il principale materiale da costruzione, doveva risultare ovvio che i volumi di solidi simili sono proporzionali ai cubi delle altezze.
Il concetto di figura inscritta in un'altra era noto (Tav. VII, fig. M), come pure quello di linea tangente, retta o curva. Queste figure all'interno di altre figure mostrano anche l'uso che la matematica babilonese faceva dell'additività delle aree unita alla similitudine quadratica. Si poteva così facilmente dimostrare, per esempio, che nella Tav. VII, fig. M1 le aree dei quadrati interni sono necessariamente uguali a 1/2 e 1/4, rispettivamente, dell'area del quadrato esterno, o che l'area del quadrato concavo (Tav. VII, fig. M3) è uguale a 1/4 del quadrato circoscritto (in quanto, prendendo il valore 3 per π, l'area del cerchio è 3/4 del quadrato circoscritto). Le aree dei segmenti doppi e delle lunule (Tav. VII, figg. E2-E4) si potevano calcolare in modo analogo.
La regola del triangolo rettangolo (hd5ha1hb) e la sua generalizzazione a tre dimensioni erano note in Mesopotamia mille anni prima di Pitagora, così com'era nota una regola analoga per trapezi suddivisi in parti equivalenti parallelamente alla base (2hd5ha1hb). Erano anche conosciute formule generali per generare triangoli rettangoli razionali (e forse anche trapezi suddivisi), come pure per generare trapezi suddivisi da altri trapezi per mezzo di un metodo di composizione che è di solito attribuito a Diofanto. Si sapevano inoltre costruire figure con lati razionali a partire da altre, incollando per esempio rettangoli i cui lati sono in rapporto razionale e triangoli rettangoli (Tav. VII, fig. C4). I problemi relativi a triangoli suddivisi in strisce (Tav. VII, figg. N1-N2) dimostrano che si sapeva calcolare il numero di parametri indipendenti in una data figura piana. Per esempio, un triangolo con 5 strisce parallele è completamente determinato se il numero di segmenti più il numero di date aree parziali è uguale a 6. Altre costruzioni (Tav. VII, figg. N3 e P3) suggeriscono che il concetto di procedimenti ricorsivi potenzialmente infiniti potesse essere familiare ai geometri babilonesi (v. fig. 11).
La potente tecnica matematica della generalizzazione è un'invenzione babilonese, come mostrano gli esempi dei trapezi e dei quadrilateri suddivisi (Tav. VII, figg. O2-O4), e la presenza in alcuni testi di poligoni regolari a 3, 4, 5, 6 o 7 lati. Un'altra tecnica importante era la permutazione di dati e incognite; essa permetteva approcci diversi a uno stesso problema geometrico. Infine, una particolarità della geometria babilonese è l'uso di ipotesi manifestamente false nel caso in cui queste potessero facilitare invece di danneggiare i calcoli a seguire. Esempi sono l'uso sistematico del valore approssimato 3 per π, la scelta frequente di un lato invece dell'altezza nel calcolo dell'area di un triangolo o di un trapezio, e perfino, sporadicamente, l'uso di una formula manifestamente errata per l'area di un quadrilatero, come nel caso di un quadrilatero suddiviso nei due sensi (Tav. VII, fig. O4).
Fin dagli inizi nel periodo degli esordi della scrittura alla fine del IV millennio, e per tutta la sua storia, la matematica mesopotamica sembra orientata verso le applicazioni; essa aveva lo scopo di insegnare a futuri scribi e amministratori come trattare in modo efficace e corretto calcoli complicati con numeri e misure espresse in tutti i diversi sistemi cuneiformi di notazione. A quanto pare, la geometria non era studiata per sé stessa, ma soltanto perché era una fonte di problemi interessanti che sollecitavano l'intuizione visiva. Non c'è traccia di impostazione assiomatica nella geometria babilonese; non sono mai dati né definizioni né assiomi, e né enunciati o dimostrati teoremi. Vi sono tuttavia molte indicazioni che mostrano come la matematica, e in particolare la geometria, fossero insegnate in modo metodico nelle scuole paleobabilonesi, anche se questa circostanza sembra in contrasto con l'impressione che danno a prima vista le traduzioni più diffuse di testi matematici di una certa grandezza. Questa impressione falsa si spiega col fatto che la maggior parte dei testi conosciuti o sono 'estratti', cioè copie fatte da studenti su tavolette di argilla di uno o più problemi tratti dalla collezione verosimilmente più completa dell'insegnante, o sono una raccolta di seconda mano più o meno sistematica di quelle copie.
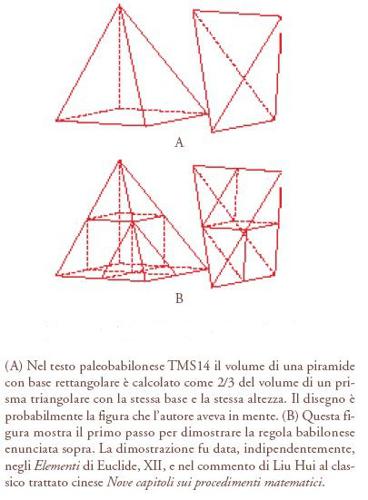
Le poche tavolette di una certa grandezza e di contenuto matematico che sembrano essere originali e non raccolte di problemi noti sono ben organizzate, e si tratta in generale di 'testi tematici', 'testi topici' o 'testi seriali'. In un 'testo tematico' sono dati esempi di complessità crescente di un'idea matematica, il tema, appunto. Un 'testo topico' è simile, ma vi possono essere trattati vari temi strettamente collegati tra loro. Questi testi sono più o meno concisi, ciascuno dei problemi ivi contenuti può constare di una sola domanda, di una domanda e relativa risposta, oppure di una domanda, del procedimento di soluzione, della risposta e della verifica. Un 'testo seriale', infine, è un testo a tema estremamente conciso, con molte piccole variazioni su un tema di carattere generale, e dunque è spesso molto poco interessante. In questo modo, la matematica babilonese scelse di operare sulla base di testi tematici contenenti problemi di complessità gradualmente crescente: in un certo senso ciò costituisce un metodo deduttivo, benché diverso dall'impostazione assiomatica, basata su definizioni, assiomi, teoremi e dimostrazioni, tipica della geometria greca (v. oltre). Inoltre nella matematica babilonese si ha spesso una verifica delle risposte ottenute; legata al metodo di verifica era poi la tecnica delle permutazioni di dati e incognite di cui abbiamo parlato in precedenza. Abbiamo un esempio isolato di un testo paleobabilonese che suggerisce come poteva essere dimostrata una difficile proposizione, nel quale si tratta di provare che il volume di una piramide è un terzo del prodotto della base per l'altezza: la dimostrazione sembra basarsi su un'ingegnosa suddivisione di un prisma con base e altezza equivalenti a quelle della piramide (fig. 14). In generale, le dimostrazioni venivano verosimilmente fatte oralmente dagli insegnanti, probabilmente utilizzando figure disegnate per terra o sui muri.
La matematica dell'Antichità: l'eredità comune
L'influenza della tradizione mesopotamica sullo sviluppo della matematica in Egitto, in Grecia o in Cina è ancora un'ipotesi controversa, in quanto non è possibile dimostrare se e quanto questa influenza sia stata decisiva: si possono solo fare congetture, più o meno fondate. Tuttavia, il lavoro storiografico svolto negli ultimi due decenni del Novecento, che ha reso disponibili numerosi testi matematici cuneiformi e ha permesso di proporre revisioni significative di vecchie interpretazioni, con la conseguente comparsa delle prime rassegne di ampia portata della storia della matematica mesopotamica, rende più facile l'analisi di tale ipotesi. Un modo per affrontare il problema può essere quello di cercare di trarre conclusioni da un confronto punto per punto degli argomenti trattati e dei metodi usati nei testi matematici mesopotamici ed extramesopotamici.
I più antichi testi matematici egizi conosciuti, i papiri matematici ieratici, sono all'incirca del periodo del Medio Regno (2000-1630), come dire coevi dei testi paleobabilonesi. Le differenze più evidenti risiedono nell'uso della scrittura ieratica, nel sistema di numerazione (è usato quello decimale), negli algoritmi per la moltiplicazione e la divisione e nel modo di contare con le frazioni (si usano somme di unità frazionarie). I più ampi testi ieratici conosciuti, il papiro Rhind e i papiri matematici di Mosca, sono però, com'è il caso per i più noti testi cuneiformi di una certa mole, raccolte di parti di altre opere. In questi papiri sono cioè riuniti, in modo piuttosto caotico, parti di varia lunghezza tratte da opere più strutturate. Non sono perciò manuali che contengono un'esposizione particolareggiata della matematica egizia, né possono servire a dare un'idea precisa della portata di questa matematica nel II millennio. Tuttavia, anche in questa prospettiva limitata vi sono riscontri che permettono di concludere che le idee e i metodi dell'antica matematica babilonese erano in larga misura conosciuti anche in Egitto.
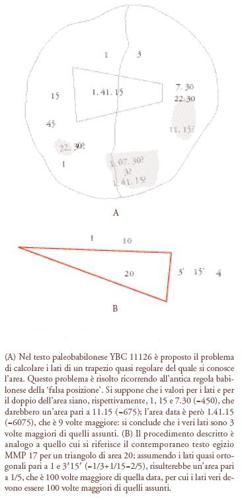
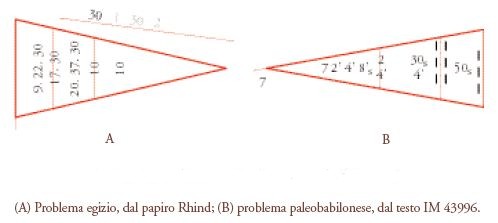
Il problema 17 del papiro di Mosca (fig. 15B), per esempio, su un triangolo avente una data area (20) e un dato rapporto tra i lati (1:3′15′), può essere confrontato con un esercizio simile che si trova nel testo paleobabilonese Yale Babylonian Collection 11126, una tavoletta che riporta una figura trapezoidale e che illustra probabilmente il problema nel caso in cui sono dati l'area e il rapporto tra tre lati (fig. 15A). Nel problema 53 del papiro Rhind invece un triangolo è diviso in tre strisce parallele (fig. 16A), e una divisione analoga compare nella tavoletta paleobabilonese, Iraq Museum 43996 (fig. 16B). In entrambi i casi i triangoli sono orientati nella direzione della scrittura, da destra a sinistra in un caso, da sinistra a destra nell'altro. L'area delle tre strisce, come pure la lunghezza di alcuni lati, è indicata in entrambi i disegni, mentre quella degli altri, incognita, è denotata con linee al posto di numeri. Si può dimostrare che i numeri espressi nelle due figure sono stati ricavati con molta cura e usando gli stessi metodi. Le aree delle tre strisce stanno approssimativamente nel rapporto 30:20:10 nel triangolo babilonese, e 50:30:8 in quello egizio. Vi sono numerosi altri evidenti paralleli tra i problemi ieratici egizi e quelli paleobabilonesi: essi riguardano alcuni tipi di equazioni lineari, distribuzioni di proporzionalità dirette e inverse e problemi di progressioni aritmetiche. Particolarmente interessante è il problema 10 del papiro matematico di Mosca, erroneamente interpretato come un problema relativo a una semisfera (un 'canestro'), ma che in realtà riguarda il calcolo dell'area di un semicerchio con un metodo che differisce da quello babilonese solo nella scelta del valore di π/4 (8/9×8/9 invece di 3/4).
Nei papiri matematici egizi demotici (periodi ellenistico e romano) si fa uso dei numeri decimali e si esprimono le frazioni nel modo tradizionale egizio, cioè come somme di frazioni unitarie; le operazioni con le frazioni sono tuttavia svolte tramite frazioni vere e proprie (a/b) o frazioni sessagesimali. È notevole il fatto che i problemi considerati nei papiri demotici coincidono largamente con problemi molto comuni della matematica babilonese: sistemi di equazioni lineari o quadratiche; problemi del tipo 'palo contro un muro', che fanno intervenire triangoli rettangoli; figure dentro figure; volume di una piramide (calcolato correttamente); volume di un tronco di cono circolare ('l'albero di un'imbarcazione', errato); suddivisioni di trapezi in strisce parallele; approssimazioni di radici quadrate, e così via. L'area del cerchio è valutata in 3/4 del quadrato del diametro, cioè assumendo per π il valore 3. L'uso implicito del sistema sessagesimale è particolarmente evidente nel papiro Cairo (III sec. a.C.), nel caso del problema 23, per esempio, in cui una somma di più frazioni unitarie, 1 2′4′8′, è convertita in un'altra somma dello stesso tipo, 1 6′′30′120′, anche se non sarebbe necessario; la spiegazione è che, riscrivendo in termini di frazioni sessagesimali, 1 2′4′8′=1;30+;15+;07.30=1;52.30=1;50+;02+;00.30 alla fine risulta 1 6′′30′120′. In ultimo, nei papiri matematici greci trovati in Egitto, in genere molto simili ai papiri demotici, i problemi considerati appartengono quasi senza eccezione al repertorio dei problemi comuni della matematica babilonese. Un esempio interessante, fornito dal papiro IFAO 88, è il problema di raddoppiare ripetutamente un capitale iniziale: 5 dracme dopo 30 raddoppi diventano 447392 talenti e 2560 dracme (valore giusto). Il calcolo è analogo a quello del testo paleobabilonese di Mari M. 8613, dove un chicco d'orzo raddoppiato 30 volte di seguito cresce fino a 2737 talenti, 32 e 1/3 scudi e 4 chicchi d'orzo.
I primi geometri greci, che avevano probabilmente familiarità con gran parte della tradizione matematica mesopotamica, trasformarono completamente questa eredità intellettuale. Forse a causa della scoperta delle grandezze incommensurabili essi rifiutarono i metodi dei loro predecessori, anche se non i risultati che questi avevano ottenuto. Le dimostrazioni rigorose basate su definizioni astratte e su assiomi assunsero il ruolo che nella matematica babilonese aveva il metodo, concettualmente più semplice, di ripercorrere all'inverso un algoritmo con valori numerici dati per controllare i valori ottenuti. In questa prospettiva, varie parti degli Elementi di Euclide si possono considerare tentativi di dimostrare come una parte consistente dell'algebra delle misure, della geometria e della teoria dei numeri babilonesi potesse rientrare nel quadro non numerico della matematica greca. Un esempio che dimostra come si sia ottenuta questa trasformazione è la riformulazione di alcuni punti fondamentali dell'algebra 'metrica' babilonese contenuta nel Libro II degli Elementi. Nella prop. 4, per esempio, si dimostra che se la somma di due quadrati e la somma dei lati (fig. 17A) sono note, allora è noto anche il rettangolo (cioè il prodotto) dei lati, mentre nella successiva prop. 5 si dimostra che se il rettangolo e la somma dei lati sono noti, allora i lati si possono determinare (fig. 17B): presi insieme, questi risultati si possono considerare una dimostrazione 'teorica' di come risolvere due dei principali sistemi di equazioni quadratico-lineari babilonesi. Altri metodi 'costruttivi' sono esposti nella prop. 9 e nella prop. 14. Nella prima (fig. 18A) si suppone che i lati incogniti siano i cateti di un triangolo rettangolo e che la somma dei loro quadrati sia il quadrato dell'ipotenusa; e si dimostra che se sono noti la diagonale e la somma dei cateti allora sono noti anche i cateti (e si possono costruire con riga e compasso). Il metodo qui potrebbe essere lo stesso usato in un esercizio paleobabilonese (BM 13 901, 8), mentre quello delle prop. 4 e 5 è lo stesso di un esercizio tardobabilonese (BM 34 568, 10). Analogamente (fig. 18B), la figura che illustra la prop. 14 si può spiegare come una soluzione costruttiva del problema di trovare due lati quando sono noti il loro prodotto (come dire l'area del rettangolo costruito con essi) e la loro somma (Euclide considera in realtà un problema leggermente diverso, ma la figura e l'idea sono le stesse). Si possono stabilire molti altri chiari paralleli tra importanti risultati della matematica greca e di quella paleobabilonese. Ci limitiamo a ricordare la regola dei triangoli rettangoli, erroneamente attribuita a Pitagora, le lunule di Ippocrate, i volumi delle piramidi nel Libro XII degli Elementi, la divisione delle figure nell'opera di Erone e di altri, e soprattutto alcune idee e metodi dell'aritmetica di Diofanto.
In conclusione, anche se non sono stati ancora scoperti testi matematici egizi del IV o del III millennio, è ragionevole supporre che lo sviluppo delle tecniche di calcolo sia avvenuto di pari passo in Egitto e in Mesopotamia. Possono addirittura esserci stati scambi di idee e metodi, come suggerisce il fatto che, come mostrano gli esempi riportati sopra, le differenze più rilevanti tra i molti testi matematici paleobabilonesi e i pochi papiri matematici egizi dello stesso periodo riguardano essenzialmente il ricorso a basi di numeri differenti. Del periodo tardobabilonese ci sono pervenuti solo pochi testi, ma sono sufficienti a dimostrare che la tradizione matematica paleobabilonese si era conservata essenzialmente intatta, subendo solo qualche variazione superficiale di stile. Un ampio testo matematico demotico egizio del III sec. a.C. dimostra in modo piuttosto chiaro che la matematica egizia di quel periodo aveva molto in comune con la matematica tardobabilonese, compreso il contare con frazioni sessagesimali. I Greci, che secondo la leggenda da loro stessi tramandata avevano appreso la geometria dagli Egizi, ebbero una notevole familiarità con gran parte della tradizione matematica babilonese, anche se la relegavano nel ruolo ancillare di matematica pratica. Se si ammette che i matematici greci lavorassero all'interno della tradizione mesopotamica, vengono meno alcune difficoltà che nascono nello studio della matematica greca, come la questione delle origini oppure la scelta degli argomenti trattati. È inoltre possibile che questa tradizione mesopotamica abbia interagito con la matematica cinese intorno al I millennio, come suggerisce la scelta degli argomenti e dei metodi del classico Nove capitoli, il più antico testo cinese di matematica a noi pervenuto, il quale si può far risalire all'epoca della dinastia Han (206 a.C. - 220 d.C.). Nella forma in cui ci è noto questo testo contiene materiale più avanzato di quanto non sia quello del corpus babilonese in nostro possesso. Gli argomenti trattati sono però gli stessi, e il tipo di problemi e i metodi di risoluzione si corrispondono in modo così puntuale che è ovvio supporre una notevole interazione tra la matematica cinese e quella babilonese in qualche periodo storico. Deboli ma innegabili tracce di quella tradizione si possono ancora trovare nell'opera di alcuni grandi matematici islamici, come pure, in Occidente, in numerosi e ben noti testi matematici prerinascimentali.
Bibliografia
fonti
Englund 1996: Englund, Robert K., The proto-cuneiform texts from diverse collections, with a contribution by Roger J. Matthews, Berlin, Gebr. Mann Verlag, 1996.
Friberg 1997: Friberg, Jöran, Five fragments of Late Babylonian extended tables of reciprocals, in: Cuneiform texts in the Metropolitan Museum of Art, edited by Ira Spar, New York, Metropolitan Museum of Art, 1997.
Neugebauer 1945: Mathematical cuneiform texts, edited by Otto Neugebauer and Abraham Sachs, New Haven (Conn.), Published jointly by the American Oriental Society and the American Schools of Oriental Research, 1945.
studi
Belmont 1998: Belmont, Eleanor Robson, Mesopotamian mathematics, 2100-1600 BC. Technical constants in bureaucracy and education, New York, Clarendon Press, 1998.
Damerow 1995: Damerow, Peter - Meinzer, Hans P., Computertomographische Untersuchung ungeöffneter archaischer Tonkugeln aus Uruk W 20987,9, W 20987,11 und W 20987,12, "Baghdader Mitteilungen", 26, 1995, pp. 7-33, tav. 1-4.
Friberg 1986: Friberg, Jöran, The early roots of Babylonian mathematics; 3, Three remarkable texts from ancient Ebla, "Vicino Oriente", 6, 1986, pp. 3-25.
‒ 1987-90: Friberg, Jöran, Mathematik, in: Reallexikon der Assyriologie, hrsg. von Erich Ebeling und Bruno Meissner, Berlin-New York, W. de Gruyter, 1928-; v. VII, 1987-1990, pp. 531-585.
‒ 1993: Friberg, Jöran, On the structure of cuneiform metrological table texts from the 1st millennium, "Grazer Morgenländische Studien", 3, 1993, pp. 383-405.
‒ 1994: Friberg, Jöran, Preliterate counting and accountig in the Middle East. A constructively critical review of Schmandt-Besserat's Before Writing, "Orientalistische Literaturzeitung", 89, 1994, pp. 477-502.
‒ 1996: Friberg, Jöran, Pyramids and cones in cuneiform and other mathematical texts. New hints of a common tradition in ancient mathematics, "Proceedings of the Cultural History of Mathematics", 6, 1996, pp. 80-95.
‒ 1997a: Friberg, Jöran, 'Seed and reeds continued'. Another metro-mathematical topic text from Late Babylonian Uruk, "Baghdader Mitteilungen", 28, 1997, pp. 251-635; 45-46.
‒ 1997b: Friberg, Jöran, Round and almost round numbers in proto-literate metro-mathematical field texts, "Archiv für Orientforschung", 44, 1997, pp. 1-58.
Høyrup 1990: Høyrup, Jens, Algebra and naive geometry. An investigation of some basic aspects of Old Babylonian mathematical thought, "Altorientalische Forschungen", 17, 1990, pp. 27-69; 262-354.
‒ 1996a: Høyrup, Jens, Changing trends in the historiography of Mesopotamian mathematics. An insider's view, "Historia Scientiarum", 34, 1996, pp. 1-32.
‒ 1996b: Høyrup, Jens, The finer structure of the Old Babylonian mathematical corpus. Elements of classification, with some results, Roskilde, Roskilde University Centre, 1996.
‒ 1996c: Høyrup, Jens, The fours sides and the area. Oblique light on the prehistory of algebra, in: Vita mathematica. Historical research and integration with teaching, edited by R. Calinger, Washington (D.C.), Mathematical Association of America, 1996, pp. 45-65.
Nemet-Nejat 1993: Nemet-Nejat, Karen Rhea, Cuneiform mathematical texts as a reflection of everyday life in Mesopotamia, New Haven (Conn.), American Oriental Society, 1993.
Neugebauer 1969: Neugebauer, Otto, Vorlesungen über die Geschichte der antiken mathematischen Wissenschaften, 2. unver. Aufl., Berlin-New York, Springer Verlag, 1969 (1. ed.: 1934).
Nissen 1993: Nissen, Hans J. - Damerow, Peter - Englund, Robert K., Archaic book-keeping. Early writing and techniques of economic administration in the ancient Near East, Chicago (Ill.), University of Chicago Press, 1993.