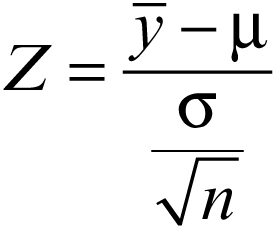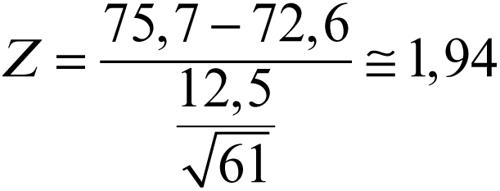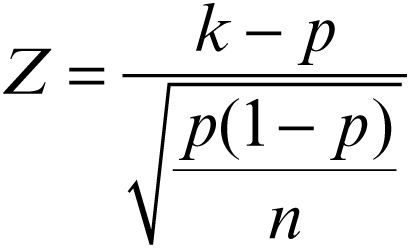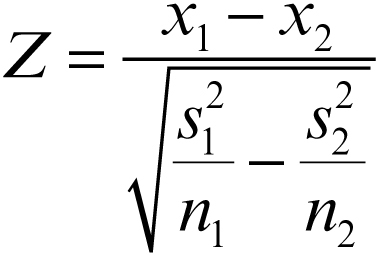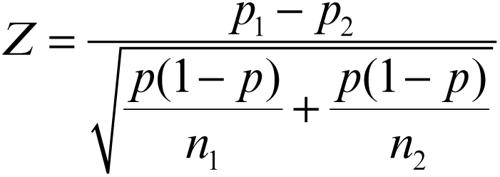verifica delle ipotesi
verifica delle ipotesi
verifica delle ipotesi in statistica inferenziale, procedura atta a confermare o rifiutare una ipotesi relativa a una popolazione sulla base dei dati ricavati da un → campione oppure atta a stabilire la significatività della differenza tra i parametri o le distribuzioni di due diversi campioni. A seconda dei casi che si vogliono sottoporre a ipotesi, sono messi in atto protocolli definiti, che mettono a confronto le ipotesi formulate (l’ipotesi nulla e la sua ipotesi alternativa; → ipotesi) con le distribuzioni statistiche teoriche che si suppongono valide per la popolazione intera (→ distribuzione). Infatti, poiché non è possibile effettuare, per motivi pratici, di costo o di tempi, esperimenti su tutti i casi possibili o sull’intera popolazione, un esperimento o una rilevazione statistica riguardano necessariamente un numero limitato di casi, e cioè un campione. Il problema riguarda perciò la probabilità che i dati ricavati dal campione possano estendersi all’intera popolazione.
A priori, selezionato il campione, deve quindi essere progettato un → test statistico che, in termini numerici e a un determinato livello di → significatività, stabilisca le zone di accettazione e di rifiuto dell’ipotesi nulla.
Le situazioni nelle quali si effettua una verifica delle ipotesi sono tra loro molto diverse e occorre almeno distinguere se esse riguardano grandi campioni (n ≥ 30), per i quali si può assumere come distribuzione teorica di riferimento quella normale (→ distribuzione normale), oppure piccoli campioni, per i quali si fa riferimento ad altre distribuzioni (per esempio, la distribuzione t di → Student). Si opera inoltre la seguente distinzione:
• se la verifica riguarda il confronto tra due differenti distribuzioni, allora i test si dicono test non parametrici (si veda per esempio → chi-quadrato);
• se la verifica riguarda parametri quali la media o la percentuale di un particolare carattere di un campione e si vuole confrontare il loro valore con quello della popolazione con distribuzione nota (generalmente una distribuzione normale) oppure riguarda il confronto tra i parametri di due campioni, allora i test statistici utilizzati si dicono test parametrici e ne sono qui riportati alcuni casi (si veda anche → verosimiglianza).
Significatività di una media
Si vuole valutare la significatività di una media per un campione di dimensione n ≥ 30 e si suppone di conoscere lo scarto quadratico medio σ della distribuzione normale della popolazione stessa. Del campione, estratto da tale popolazione, si determina la → media ȳ. Se si vuole verificare l’ipotesi nulla H0 che la media della popolazione sia μ (a un livello di significatività α = 5%) si utilizza il test statistico:
Se non è noto lo scarto quadratico medio della popolazione, a esso si sostituisce s, radice quadrata della → varianza campionaria. Stabilito un livello di significatività (per esempio α = 5%), si consulta la tavola che fornisce i valori della funzione di ripartizione della variabile normale Φ(y) = P(Z ≤ y) e si accetta o rifiuta di conseguenza l’ipotesi nulla formulata. Al livello α = 0,05 si ha:
Se per esempio si è registrato che il voto medio riportato all’esame di stato in una provincia è stato 72,6/100, mentre in una determinata commissione d’esame, che ha esaminato 61 candidati, il voto medio è stato 75,7/100, con uno scarto quadratico medio uguale a 12,5, e si vuole stabilire se tale differenza di medie sia o meno significativa, si effettua il calcolo:
Poiché tale valore è minore di 1,96, si accetta l’ipotesi nulla che non ci sia differenza significativa tra la media riportata nel campione costituito dalla singola commissione d’esame e la media generale.
Significatività di una percentuale
Di una popolazione si conosce la frequenza relativa p (con 0 < p < 1) di un carattere, eventualmente espresso in percentuale. Di un campione di dimensione n estratto dalla popolazione risulta una percentuale di carattere uguale a k (con 0 < k < 1). In questo caso si utilizza il test statistico
e per la regola di decisione si procede come per la valutazione della significatività di una media.
Significatività del confronto tra due medie
Di due campioni di dimensioni n1 e n2 si conoscono le rispettive medie x1 e x2 e i rispettivi scarti quadratici medi s1 e s2 (valutati sul campione: → varianza campionaria). Il test statistico utilizzato in questo caso è
che si confronta con la distribuzione normale.
Significatività del confronto tra due percentuali
Di due campioni di dimensioni n1 e n2, estratti dalla stessa popolazione, si conoscono le frequenze relative p1 e p2 di uno stesso carattere (espresse in percentuale) e si vuole verificare l’ipotesi che non ci sia differenza significativa tra esse. In questo caso, si può stimare come percentuale della popolazione la media p delle due percentuali
e utilizzare il test statistico
Per la regola di decisione si procede come per la valutazione della significatività di una media.