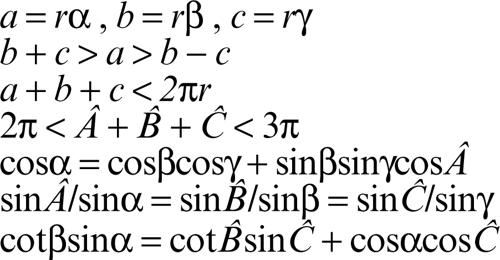trigonometria

trigonometria

trigonometria branca della matematica che studia le relazioni tra misure lineari e misure angolari; essa studia quindi le → funzioni goniometriche (dette anche funzioni circolari) e, tramite queste, la «risoluzione» dei triangoli, ossia la determinazione dei loro elementi (lati e angoli) conoscendone alcuni.

Origini e sviluppo

Poiché il triangolo è la configurazione di punti più elementare, la trigonometria, intesa come studio delle relazioni tra gli elementi di un triangolo, ha origini antichissime. Alcune proprietà erano già note agli antichi egizi, che certamente conoscevano, in alcuni casi particolari, le relazioni tra i lati di un triangolo rettangolo, poi generalizzate nel teorema di Pitagora, e ai babilonesi. Tali conoscenze trassero origine dallo studio dei fenomeni astronomici sia per finalità pratiche (orientamento durante la navigazione, misurazione del tempo, previsione delle stagioni) sia per finalità speculative o di carattere magico-religioso.

In epoca greca classica, si deve all’astronomo Ipparco di Nicea, nel trattato sulle Corde in un cerchio, la prima compilazione di tavole che mettono in relazione la lunghezza delle corde di un cerchio con i corrispondenti angoli al centro (cioè, con linguaggio moderno, l’ampiezza di un angolo e il doppio del → seno dell’angolo di metà ampiezza): è in questa tavola delle corde che probabilmente comparve per la prima volta in modo sistematico l’uso della suddivisione dell’angolo giro in 360 parti (mutuato dal sistema di numerazione sessagesimale babilonese e approssimazione della durata in giorni dell’anno solare). La trigonometria greca si sviluppò sulla base dell’impostazione di Ipparco e prese come suo riferimento proprio la relazione tra archi e corde sottese. Importanti contributi furono dati da Menelao di Alessandria (→ Menelao, teorema di) che, nel i secolo d.C., approfondì anche problemi di trigonometria sferica mostrando che, differentemente dai triangoli nel piano di Euclide, la somma delle ampiezze degli angoli di un triangolo sferico supera l’angolo piatto. Poco più tardi (attorno alla metà del ii secolo), l’opera più matura elaborata in ambito greco fu la Sintassi matematica di Claudio Tolomeo di Alessandria, che, nel mondo arabo e successivamente, divenne nota col titolo di Almagesto (la raccolta «maggiore»). Egli calcolò più accurate tavole delle corde e, sulla base di quello che sarà detto teorema di → Tolomeo, stabilì alcune formule che equivalgono a quelle che oggi sono dette formule di addizione e sottrazione per seno e coseno (che talvolta sono infatti anche dette formule di Tolomeo). In ambito arabo e indiano, la trigonometria ebbe un lento ma deciso sviluppo: dal vi al xii secolo, con i Siddhanta (sommari) di Aryabhata, Brahmagupta e Bhāskara, si passò definitivamente a considerare il seno dell’angolo (e non più la corda dell’angolo doppio), si introdussero nuove linee trigonometriche, quali il coseno, la tangente, la cotangente, la secante e la cosecante, furono compilate tavole con approssimazioni sempre più raffinate e fu dimostrato il teorema dei → seni. In Europa, il primo a trattare la trigonometria come disciplina autonoma di studio fu nel Quattrocento l’astronomo, astrologo e matematico tedesco Johannes Müller da Königsberg, il cui nome fu latinizzato in Joannes de Regiomonte e quindi italianizzato in Regiomontano, che, durante la sua permanenza a Roma, scrisse il trattato De triangulis omnimodus. La definitiva sistemazione della trigonometria, con l’introduzione delle funzioni goniometriche, il loro sviluppo in serie e i relativi simboli ancora oggi in uso, si deve infine a Eulero con il suo Introductio in analysin infinitorum (1748). In esso egli stabilisce anche il sorprendente e fecondo collegamento tra numeri complessi, funzione esponenziale e funzioni goniometriche (→ Eulero, formula di).

Oggetti di studio della trigonometria

Se ci si limita agli angoli acuti, le funzioni goniometriche possono essere definite in relazione al solo triangolo rettangolo. Il seno (coseno) di un angolo acuto è infatti il rapporto tra il cateto opposto (adiacente) a tale angolo e l’ipotenusa; la tangente di un angolo acuto è il rapporto tra il cateto opposto a tale angolo e quello adiacente. Per la definizione delle funzioni goniometriche come funzioni di variabile reale, occorre invece riferirsi alla circonferenza goniometrica (donde la locuzione funzioni circolari); a partire da essa si definiscono le funzioni goniometriche: il → coseno, il → seno, la → tangente (definita come rapporto tra seno e coseno), la → cotangente, la → secante, la → cosecante e le relative → funzioni goniometriche inverse.

Le funzioni goniometriche sono funzioni periodiche e non lineari e tra esse intercorrono svariate relazioni che danno luogo a numerose formule. Tra esse è fondamentale la formula, valida per ogni x ∈ R:

Le formule più utilizzate nella risoluzione di problemi che coinvolgono la trigonometria sono quelle relative agli angoli associati, quelle di addizione e sottrazione di angoli, quelle di duplicazione e triplicazione, di bisezione, delle potenze di angoli, le formule parametriche, di prostaferesi. A queste si aggiungono quelle ricordate con il nome di chi le ha introdotte e dimostrate, quali per esempio le formule di Werner. Queste formule sono riportate nelle tavole delle principali relazioni di trigonometria.

I valori di seno, coseno, tangente e cotangente, in corrispondenza dei valori degli angoli di ampiezza compresa fra 0 e π/2, scelti a opportuni intervalli regolari, sono elencati in apposite tavole numeriche, dette → tavole trigonometriche. Di questi, i principali sono riportati nelle tavole delle principali relazioni di trigonometria. Finché ci si limita alle relazioni tra misure lineari e angolari, la trigonometria è anche detta goniometria. In senso stretto, infatti, per trigonometria deve intendersi lo studio delle relazioni in un triangolo. Per questo, si veda → triangolo, risoluzione di un nonché le tavole delle principali proprietà elementari delle figure piane.

Trigonometria piana

Parte della trigonometria applicabile ai triangoli piani, che stabilisce come determinare i sei elementi del triangolo quando se ne conoscano tre (di cui uno almeno sia un lato): per questo, si veda → triangolo, risoluzione di un.

Trigonometria sferica

Parte della trigonometria applicabile ai triangoli a lati curvilinei tracciati su una sfera e che permette di risolvere problemi analoghi a quelli della trigonometria piana, cioè di determinare i sei elementi di un → triangolo sferico. Detti a, b, c le lunghezze dei lati curvilinei, Â, B̂, Ĉ le misure degli angoli rispettivamente opposti ai lati (misurati tracciando le tangenti ai lati del triangolo sferico nei punti d’intersezione) e α, β, γ le misure degli angoli espressi in radianti fra i tre raggi r condotti dal centro della sfera ai vertici del triangolo (e che sottendono rispettivamente a, b, c), le relazioni fondamentali della trigonometria sferica sono le seguenti:

e quelle che si ottengono da queste permutando i ruoli in ciascuna terna degli elementi che vi compaiono (si veda anche → Borda, formule di).

Nel caso del triangolo trirettangolo si ha: