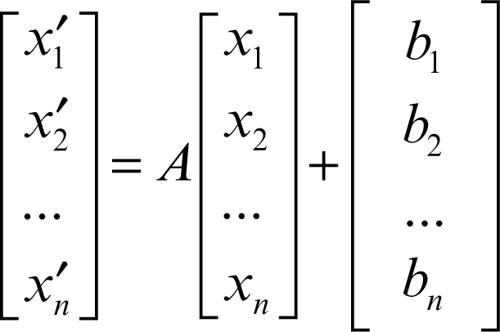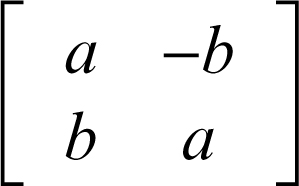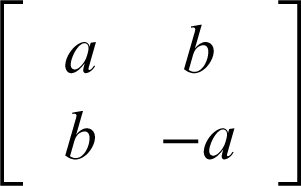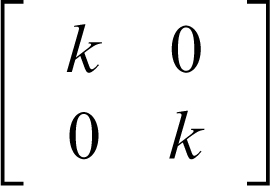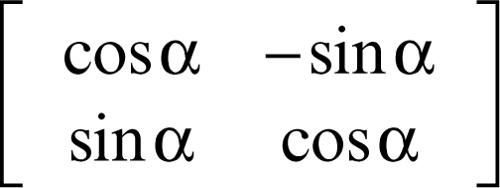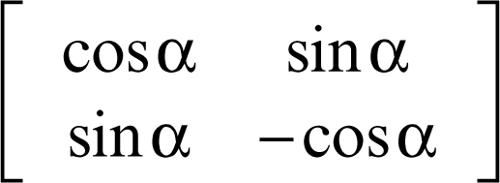trasformazione geometrica, matrice di una

trasformazione geometrica, matrice di una

trasformazione geometrica, matrice di una in uno spazio affine o metrico n-dimensionale, una trasformazione geometrica che sia una collineazione (che cioè mantenga l’allineamento dei punti) è espressa da equazioni matriciali del tipo

con A matrice quadrata di ordine n non singolare, cioè tale che det(A) ≠ 0. La matrice con i termini noti b_i, …, b_n esprime la componente di → traslazione della trasformazione. Tutte le altre caratteristiche della trasformazione sono descritte dalla sola matrice A, che ne caratterizza il tipo. Una generica matrice A non singolare è quindi la matrice di una affinità avente un punto fisso in O. Ad altri particolari tipi di matrici corrispondono i diversi tipi di trasformazioni. Limitandosi alle trasformazioni geometriche collineari del piano, le seguenti matrici ne caratterizzano alcuni tipi:

• Matrice di una similitudine diretta di rapporto k = √(a² + b²)

• Matrice di una similitudine invertente di rapporto k = √(a² + b²)

• Matrice di una omotetia di rapporto k

• Matrice di una rotazione di ampiezza α

• Matrice di una simmetria con asse una retta per l’origine di inclinazione α/2