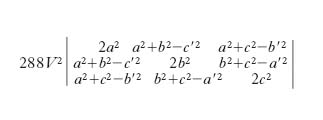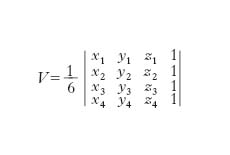tetraedro

tetraedro Il più semplice dei poliedri, che ha 4 vertici, 6 spigoli, 4 facce triangolari e può essere pensato come una piramide a base triangolare. Le mediane di un t. (ossia i segmenti che congiungono ciascun vertice con il baricentro della faccia opposta) s’incontrano in uno stesso punto, il baricentro del t., che divide ogni mediana in due parti, delle quali quella che contiene il vertice è tripla dell’altra. Le rette che passano per il centro del cerchio circoscritto a ogni faccia e che sono perpendicolari alla faccia stessa s’incontrano anch’esse in uno stesso punto, detto circocentro del t., che è il centro della sfera circoscritta al tetraedro. I 6 piani bisettori dei diedri del t. si incontrano anch’essi in uno stesso punto, l’incentro, che è il centro della sfera interna al t. e tangente a tutte le facce. Diversamente da quanto avviene nei triangoli, le altezze di un t., ossia le rette per ciascun vertice perpendicolari alla faccia opposta, non si incontrano in uno stesso punto; ciò avviene solo per i t. ortocentrici.

Il volume di un t. può essere ottenuto moltiplicando l’area di una delle 4 facce per la corrispondente altezza e dividendo il prodotto per 3, oppure moltiplicando la superficie totale del t. per il raggio della sfera iscritta e dividendo per 3, o anche moltiplicando le lunghezze di due spigoli opposti per la loro distanza e per il seno del loro angolo e dividendo per 6. È poi notevole la formula che dà il volume V in funzione degli spigoli: in essa a, b, c sono le misure degli spigoli uscenti da uno stesso vertice e a′, b′, c′ sono gli spigoli opposti ad a, b, c rispettivamente:

Infine l’espressione del volume del t. di vertici Pi(xi,yi,zi) con i=1, 2, 3, 4 è

T. tronco È un poliedro (➔) archimedeo costituito da 8 facce: 4 esagoni regolari e 4 triangoli equilateri. Si ottiene dal t. regolare troncandone gli angoloidi mediante piani opportuni, in modo che i tagli generino triangoli equilateri e riducano a esagoni regolari le facce triangolari preesistenti.