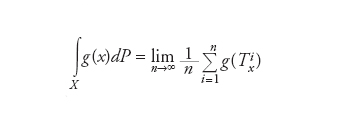teorema ergodico

di Giacomo Aletti - Enciclopedia della Scienza e della Tecnica (2008)

teorema ergodico

Giacomo Aletti

In un sistema dinamico governato da una trasformazione ergodica, la media spaziale e la media temporale coincidono quasi certamente. Matematicamente, un sistema dinamico measure-preserving è un sistema (X,✄,P,T) dove (X,✄,P) è uno spazio di probabilità e T:X→X è una trasformazione misurabile che conserva P, ossia P(T−1(A))=P(A), per ogni A in ✄. Un evento A in ✄ è detto T-invariante se è di fatto identico al suo trasformato: P(AΔT(A))=0, dove Δ è il simbolo di differenza simmetrica insiemistica. Un sistema measure-preserving (X,✄,P,T) è detto ergodico se gli unici eventi T-invarianti sono banali, ossia hanno probabilità 0 o 1. Il teorema ergodico afferma che per funzione g su un sistema ergodico (X,✄,P,T) sufficientemente regolare – g deve appartenere a L1(X,✄,P) – si ha che

formula

→ Probabilità

Vedi anche
speranza matematica S. matematica di una variabile casuale è la somma dei prodotti dei valori che essa assume per le rispettive probabilità. S. matematica di un giocatore in un gioco d’azzardo è la vincita o perdita che, in media, il giocatore deve aspettarsi a priori, in base alle probabilità degli eventi legati ... applicazione Matematica Il concetto di a. è una generalizzazione del concetto classico di funzione (➔ corrispondenza). Si parla di a. di un insieme P in un insieme Q, quando tra i due si stabilisce una corrispondenza del tipo seguente: a ogni elemento di P corrisponde un ben determinato elemento di Q, mentre un elemento ...
Categorie
Tag
Altri risultati per teorema ergodico
  • teorema ergodico
    Enciclopedia della Matematica (2013)
    teorema ergodico teorema della teoria ergodica. Poiché l’aggettivo ergodico si attribuisce a un processo in cui la media nel tempo delle grandezze fisiche che lo descrivono coincide con la media calcolata su un insieme di stati in cui il processo può trovarsi, è possibile distinguere i processi dinamici ...
Vocabolario
ergòdico
ergodico ergòdico agg. [comp. del gr. ἔργον «opera; energia» e ὁδός «via», con riferimento al «percorso» del punto che rappresenta un sistema di «energia» data] (pl. m. -ci). – In meccanica statistica, termine introdotto dal fisico L. Boltzmann...
teorèma
teorema teorèma s. m. [dal lat. tardo theorēma, gr. ϑεώρημα (propr. «ricerca, meditazione», der. di ϑεω-ρέω «esaminare, osservare»)] (pl. -i). – 1. Nella cultura classica e medievale, la «visione» sensibile o intellettiva e il relativo...