strofoide
strofoide
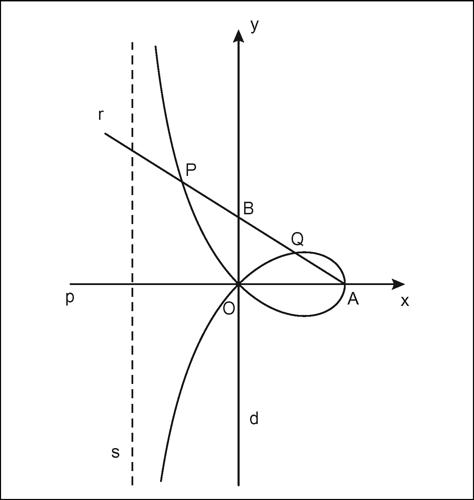
strofoide curva algebrica piana del terzo ordine, detta anche logocicla, ottenuta a partire da una retta d e da un punto A esterno alla retta, detto punto fisso. Da A si traccia la retta p, perpendicolare a d, che interseca d in O, detto polo. La strofoide è il luogo dei punti P e Q, allineati con A e con un punto B della retta d, tali che PB = BQ = OB, al variare di B sulla retta d. Fissato un riferimento cartesiano con origine in O e avente per assi le rette p e d, l’equazione cartesiana della strofoide è a(y 2 − x 2) + x(x 2 + y 2) = 0, dove a è l’ascissa del punto A. La curva, simmetrica rispetto all’asse delle ascisse, ha un nodo nell’origine e ha per asintoto la retta di equazione. La strofoide così ottenuta è detta strofoide retta; se la retta OA è obliqua rispetto alla retta d, la strofoide è detta obliqua. L’area della regione finita di piano individuata dalla strofoide retta è a2(4 − π)/2. La strofoide può essere utilizzata sia per trisecare un angolo sia per duplicare il cubo. La sua forma è simile a quella della trisettrice di Maclaurin (→ trisettrice). Il suo nome viene dal greco stróphos, indicante una cintura con un anello atto a sostenere la spada.