spirale

spirale

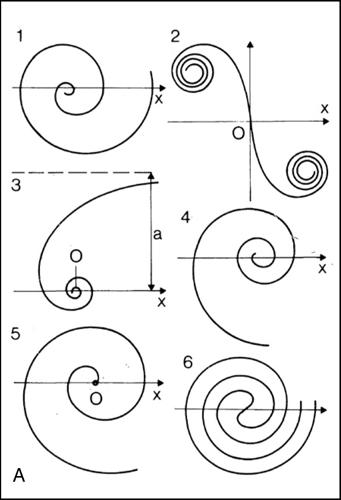
spirale classe di curve piane trascendenti aventi, da un punto di vista qualitativo, una forma simile e, generalmente, dotate di un punto detto centro o polo della spirale, a partire dal quale la curva si avvolge (o verso il quale si avvolge) in senso orario o antiorario, variando la sua distanza da esso. Si chiama spira ognuno degli archi di spirale che si individuano compiendo un giro completo sulla spirale stessa. Esistono diversi tipi di spirale, descritte da differenti equazioni.

La spirale di Archimede si ottiene tracciando una circonferenza in modo continuo e aumentando punto per punto il raggio in modo proporzionale all’angolo descritto; la sua equazione in coordinate polari è ρ = kθ, con k costante (→ Archimede, spirale di).

La spirale iperbolica è una curva piana trascendente, detta anche spirale inversa, caratterizzata dalla proprietà che in ogni suo punto le coordinate polari hanno prodotto costante. La sua equazione polare è pertanto ρ = k/θ, con k costante. È considerata in un certo senso l’inversa della spirale di Archimede in quanto le coordinate polari dei suoi punti sono inversamente proporzionali. La spirale iperbolica ha come asintoto una retta a distanza k dal polo (e quindi da un certo punto in poi non si avvolge più) ed è illimitata anche verso il polo, attorno al quale continua ad avvolgervisi all’infinito senza mai raggiungerlo.

La spirale logaritmica è una curva piana trascendente, di equazione

da cui il nome. Ogni semiretta uscente dal centro della spirale logaritmica taglia la curva secondo un angolo costante β = arctan(1/lnb) e per questa ragione la curva è detta anche spirale equiangolare. L’angolo α = arctan(lnb) è detto angolo di inclinazione e rappresenta l’angolo costante che la curva forma con ogni circonferenza di centro l’origine. Qualsiasi semiretta uscente dall’origine interseca la spirale a distanze che sono in progressione geometrica di ragione b^2π, a differenza di quanto accade per una spirale di Archimede nella quale tali distanze sono in progressione aritmetica di ragione k. La spirale logaritmica raggiunge il suo centro dopo infiniti avvolgimenti in cui la curva va progressivamente restringendosi.

Uno dei motivi dell’importanza di questa curva consiste nella sua presenza in molti fenomeni naturali. Per esempio, gli uccelli rapaci si avvicinano alla preda chiudendo una spirale equiangolare, poiché il loro angolo di vista migliore forma un determinato angolo con la direzione di volo e tale angolo costante è l’inclinazione della spirale. La spirale logaritmica è presente anche in alcune forme di conchiglie o nella disposizione delle foglie di alcune piante e per queste ragioni è detta anche spirale di crescita. Una particolare spirale logaritmica è la spirale aurea (→ sezione aurea).

La spirale lossodromica o spirale sferica è una spirale equiangolare (spirale logaritmica) tracciata su una sfera. Per esempio, nella navigazione, una rotta che taglia i meridiani secondo un angolo costante (curva → lossodromica) è costituita da un arco di spirale logaritmica.

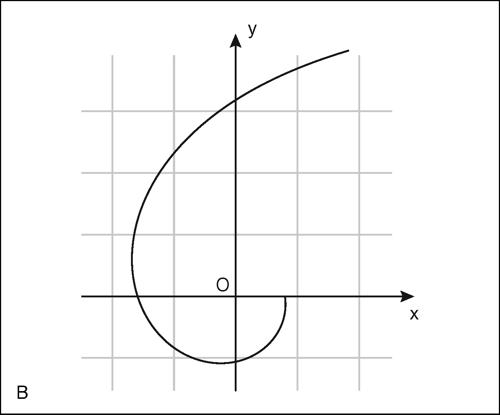
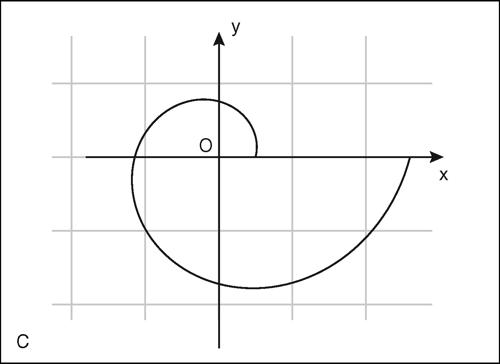
Altre curve della famiglia delle spirali sono la spirale parabolica o spirale di → Fermat, di equazione ρ² = k ²θ, la spirale di Cornu, più nota con il nome di → clotoide, e il → lituo.