modulari, sostituzioni
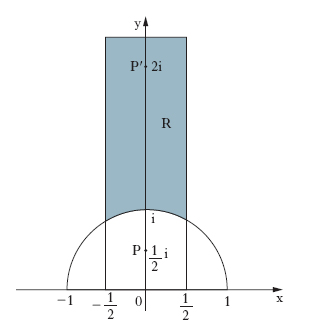
In matematica, le sostituzioni lineari su una variabile complessa z=x+iy espresse dalla formula z′=(αz+β)/(γz+δ), ove α, β, γ, δ sono numeri interi ed è αδ−βγ=1; si tratta perciò di particolari affinità circolari di Möbius (➔ affinità), che ricevono l’attributo di unimodulari o brevemente modulari in quanto αδ−βγ si chiama modulo dell’affinità. Le sostituzioni m. costituiscono un gruppo, infinito ma discontinuo, che si chiama gruppo m.; ciascuna di esse associa a ogni punto del piano complesso un nuovo punto che si dice equivalente al primo: per es., la sostituzione z′=−1/z associa al punto P (v. fig.) il punto equivalente P′. Se ora si considera la regione R del semipiano y>0 esterna alla circonferenza x2+y2=1 e compresa tra le rette x=−1/2, x=1/2, accade che due punti di R non sono mai equivalenti, mentre ogni punto del semipiano y>0 è equivalente a un punto di R: per questo motivo R si dice campo fondamentale del gruppo modulare.
Si chiama poi funzione modulare ogni funzione analitica di una variabile complessa z che rimane inalterata quando sulla z si effettui una qualunque sostituzione m.; di conseguenza, una funzione modulare è perfettamente individuata quando siano assegnati i valori che essa assume nel campo fondamentale del gruppo modulare. La teoria delle funzioni modulari ha svariate applicazioni: per es., per la risoluzione dell’equazione generale di quinto grado.