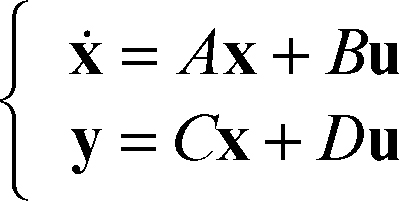sistema dinamico

sistema dinamico

sistema dinamico modello matematico di un fenomeno fisico che si evolve nel tempo. Esempi di sistema dinamico possono essere il moto dei pianeti, le oscillazioni di un pendolo, il flusso delle correnti atmosferiche, il numero di insetti che anno dopo anno popolano una certa regione, l’andamento giornaliero dei prezzi delle azioni nei mercati finanziari. Per descrivere matematicamente un sistema dinamico occorre individuare un certo numero di grandezze misurabili, cioè espresse mediante numeri reali x₁, x₂, ..., x_n, che permettano di identificare lo stato, ossia la configurazione a un certo istante t, del sistema che si vuol esaminare. Tali grandezze sono dette variabili di stato o anche semplicemente stati. L’insieme dei loro valori definisce univocamente lo stato del sistema a un dato istante t, espresso dal vettore a n componenti

che può essere pensato come un punto geometrico riferito agli assi di un sistema, in cui le coordinate corrispondono ai valori delle variabili di stato. Per esempio, lo stato di un pendolo semplice è rappresentato da un punto in uno spazio bidimensionale (un piano cartesiano) riportando sugli assi il valore dello spostamento angolare rispetto alla verticale e il valore della velocità angolare. Il numero n delle variabili di stato è detto ordine del sistema. L’insieme di tutti i possibili vettori di stato è detto spazio delle fasi del sistema dinamico. La variabile t, utilizzata per misurare il tempo che scorre, può essere pensata come un numero reale, e si parla allora di sistema dinamico a tempo continuo, oppure come un numero naturale, cioè t = 0, 1, 2, …, e allora si parla di sistema dinamico a tempo discreto. I sistemi dinamici possono interagire con l’esterno tramite delle variabili in ingresso che ne influenzano l’andamento e delle variabili in uscita che costituiscono l’aspetto del fenomeno che si desidera controllare. Le variabili in uscita sono le stesse variabili di stato (non necessariamente tutte) o una loro combinazione. Per esempio, sempre per il pendolo semplice, una variabile in ingresso può essere una forza esterna applicata sulla massa appesa e la variabile in uscita può essere lo stesso spostamento angolare rispetto alla verticale. Le variabili in ingresso e in uscita sono espresse rispettivamente con i vettori u(t) = (u₁(t), ..., u_m(t)) e y(t) = (y₁(t), ..., y_m(t)).

Da un punto di vista formale, conoscere un sistema dinamico significa conoscere una funzione ƒ che una volta assegnati il vettore di stato x₀ a un dato istante iniziale t₀ e gli ingressi u(t), permetta di determinare univocamente lo stato del sistema a ogni istante di tempo successivo: x(t) = ƒ(t₀, x₀, u(t), t).

Dati una condizione iniziale x(t₀) = x₀ e l’ingresso, l’insieme di tutti i valori x(t) ottenuti mediante l’applicazione della funzione ƒ costituisce la traiettoria o movimento del sistema dinamico passante per la condizione iniziale assegnata. Un movimento può essere pensato come una curva nello spazio n-dimensionale delle fasi, mentre in un sistema dinamico a tempo discreto un movimento è costituito da una successione di punti; un movimento costituito da un vettore di stato costante nel tempo è detto di equilibrio. Per conoscere l’operatore ƒ, si cerca di risalire a esso attraverso la formulazione di leggi di evoluzione nel tempo del sistema o equazioni della dinamica, di cui ƒ costituisce una delle possibili soluzioni. Nel caso di modelli a tempo continuo, le leggi della dinamica sono espresse mediante sistemi di equazioni differenziali ordinarie del tipo

dove il punto indica la derivata temporale. Nel caso di modelli dinamici a tempo discreto, la legge della dinamica è rappresentata sotto forma di equazioni alle differenze del tipo ƒ(x(t), x(t + 1), u(t), t) = 0. Se la funzione ƒ non dipende esplicitamente dal tempo, il sistema dinamico è detto tempo invariante (altrimenti è detto tempo variante). Se la funzione ƒ è lineare rispetto a tutte le sue variabili allora il sistema è detto lineare (altrimenti è detto non lineare). Un aspetto molto importante di un sistema dinamico è la stabilità dei suoi movimenti. A livello intuitivo, un movimento è stabile se variando di poco la condizione iniziale, con lo stesso ingresso, il movimento risultante (detto perturbato) differisce di poco dal movimento originario (detto nominale). In termini rigorosi, un movimento x̄(t) derivante da un ingresso ū(t) e da una condizione iniziale x̄₀ si dice stabile se per ogni ε > 0 esiste un δ > 0 tale che per tutti gli stati iniziali x̄₀ che soddisfano la relazione

risulta che

dove x(t) è il movimento derivante da x̄₀ e da ū(t). Se un movimento non è stabile, è detto instabile. Se un movimento è stabile e per t → ∞ il movimento perturbato tende al movimento nominale, allora il movimento è detto asintoticamente stabile (altrimenti è semplicemente stabile).

Sistemi dinamici a tempo continuo, lineari e tempo invarianti

Tali sistemi dinamici. sono esprimibili tramite il sistema di equazioni

dove lo stato x, l’ingresso u e l’uscita y sono espressi come vettori colonna, e A, B, C e D sono matrici. In particolare la matrice A è quadrata ed è detta matrice della dinamica. Se la matrice D è nulla, cioè se l’uscita non dipende direttamente dall’ingresso, il sistema è detto strettamente proprio (altrimenti è proprio). Si può dimostrare che tutti i movimenti di un sistema lineare tempo invariante hanno le stesse caratteristiche di stabilità (per esempio, sono tutti instabili o tutti stabili), per cui nel caso di questo tipo di sistemi si può genericamente parlare di stabilità del sistema (anziché del movimento). La stabilità del sistema è collegata agli autovalori λ_k della matrice A (con k = 1, …, n, dove n è l’ordine del sistema): 1) se Re(λ_k) ≤ 0 per k = 1, …, n, il sistema è stabile; 2) se Re(λ_k) < 0 per k = 1, …, n, il sistema è asintoticamente stabile; 3) se Re(λ_k) > 0 per almeno un valore di k, il sistema è instabile (teorema di Ljapunov).

Sistemi dinamici a tempo continuo, non lineari

Sistemi dinamici di grande interesse nelle applicazioni; è possibile utilizzare anche per essi la teoria dei sistemi lineari praticando la cosiddetta linearizzazione del sistema nell’intorno di una posizione di equilibrio. Sia

l’equazione della dinamica del sistema e sia x̄ un movimento di equilibrio derivante da un ingresso costante ū(t) Il sistema linearizzato consiste nello sviluppo di → Taylor del primo ordine delle equazioni della dinamica, nell’intorno del movimento di equilibrio. Esprimendo il movimento perturbato come x(t) = x̄ +δx(t), in presenza di un ingresso perturbato u(t) = + δu(t), le equazioni della dinamica del sistema linearizzato sono

È possibile esprimere le equazioni della dinamica secondo la consueta forma:

Si noti che tuttavia esse non sono espresse in termini di stato e ingresso, ma in termini di variazioni dello stato e dell’ingresso rispetto al movimento di equilibrio considerato.

Controllo di un sistema dinamico

È la procedura con cui si fornisce al sistema un ingresso adeguato a ottenere l’uscita voluta. Dal punto di vista ingegneristico, controllare un sistema dinamico può essere di qualche interesse al fine di ottenere un’uscita desiderata. Nel controllo di un sistema si dovrà anche tenere conto dei disturbi, che possono essere pensati come degli ingressi non desiderati e non controllabili che alterano lo stato del sistema. Il dispositivo che fornisce l’ingresso adeguato al sistema è detto controllore o regolatore. Per esempio, una cella frigorifera può essere schematizzata come un sistema dinamico di cui si vuole mantenere costante la temperatura: l’uscita (che è anche lo stato) è rappresentata dalla temperatura stessa, l’ingresso è il calore sottratto alla cella dal sistema di raffreddamento e il disturbo è il calore che entra dall’esterno; il controllore è il sistema elettronico che regola la potenza del sistema di raffreddamento, determinando così la quantità di calore sottratto. Se il controllore esercita la sua azione in base a una misura dell’uscita del sistema, il controllo è detto in anello chiuso, altrimenti è detto in anello aperto. La teoria del controllo costituisce una vasta branca dell’ingegneria, con numerose applicazioni in svariati campi.