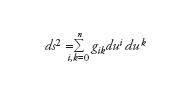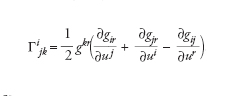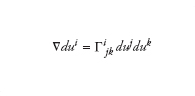simboli di Christoffel

simboli di Christoffel

Sia M una varietà dotata di una metrica riemanniana. Ricordiamo che essa si può esprimere localmente nella forma

dove (g_ik) è una matrice n×n hermitiana definita positiva che dipende dalle coordinate u¹,...,uⁿ. I simboli di Christoffel relativi alla metrica sono definiti nel modo seguente:

Per alleggerire le notazioni, si applica l’usuale convenzione secondo la quale un indice ripetuto in ogni addendo (in questo caso ‘r’) sostituisce una sommatoria ∑_r. I coefficienti g^kr sono gli elementi della matrice inversa di g_kr. I simboli di Christoffel permettono di definire la connessione di Levi-Civita, un operatore molto importante che fornisce un metodo per valutare la velocità con cui i vettori e i tensori variano sulla varietà. In simboli, l’operatore ∇ dato da

prende il nome di connessione di Levi-Civita.

→ Geometria differenziale