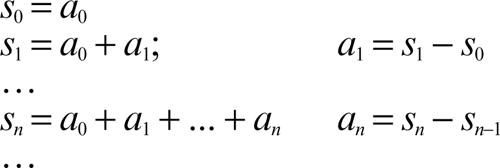serie

serie

serie successione che consente di generalizzare la nozione di somma al caso di un numero infinito di addendi. Tali addendi possono essere numeri (→ serie numerica) o funzioni (→ serie di funzioni), ma anche matrici od operatori lineari. Tra le serie numeriche si segnalano la serie armonica, la serie geometrica, la serie trigonometrica e quelle tradizionalmente riportate con il nome del matematico che le introdusse (per esempio, la serie di → Gauss, la serie di → Grandi, la serie di → Mengoli, la serie di → Riemann). Tra le serie di funzioni si segnalano le → serie di potenze e, anche in questo caso le principali serie riferibili al matematico o ai matematici che le studiarono: la serie di → Dirichlet, la serie di → Fourier, la serie di → Laurent, la serie di → Maclaurin, da cui si ricava la serie di → Gregory-Leibniz, la serie di → Mercatore, la serie di → Taylor).

Formalmente una serie può essere definita mediante una coppia di successioni {a_n}, {s_n} di elementi di uno spazio normato E, legate tra loro dalle formule

Gli elementi a_n si dicono termini della serie, mentre gli elementi s_n si dicono somme parziali o ridotte n-esime. Una serie si indica con i simboli

a prescindere dalla possibilità che a essi possa essere attribuito un significato effettivo. A volte come primo termine viene scelto quello di indice 1 se tale scelta agevola sul piano formale.

Si chiama serie subordinata a una serie data, ottenuta dalla successione a₀, a₁, ..., a_n, ..., una qualsiasi serie ottenuta da una sua sottosuccessione.

Si chiama limite di una serie il limite della successione delle somme parziali: se esiste ed è finito, la serie è convergente e tale limite S è detto somma della serie:

Se il limite è infinito la serie è divergente, mentre nel caso in cui tale limite non esista la serie è detta indeterminata o oscillante. Se E è uno spazio completo, per la convergenza della serie data è sufficiente la convergenza della serie numerica

Se questa serie è convergente la serie si dice totalmente convergente.

Si chiama resto k-esimo R_k della serie, la serie:

ottenuta a partire dalla sottosuccessione a_k+1, a_k+2, ... Rappresenta l’errore commesso se nel calcolo della somma della serie ci si arresta alla somma parziale k-esima:

(→ Lagrange, resto di; → Peano, resto di).

È anche possibile considerare una serie formale come un semplice simbolo, collegato a una “somma”, senza che ciò implichi la convergenza (si veda anche → sviluppo asintotico).

La nozione di serie si estende in varie direzioni, per esempio, a partire dalle successioni bilatere e dalle successioni multiple. I problemi fondamentali concernenti le serie sono:

• la convergenza: stabilire se a una data serie possa essere attribuita una somma (serie convergente) o no;

• la sintesi e l’analisi per serie: stabilire, per una serie convergente, una espressione chiusa per la sua somma e, viceversa, esprimere un numero o una funzione come somma di una opportuna serie;

• la rapidità di convergenza: stabilire, per una serie convergente, quanti addendi debbano essere presi in considerazione per ottenere la somma con una desiderata precisione;

• le proprietà e le operazioni: generalizzare alle serie le regole dell’algebra delle somme (associativa, commutativa, distributiva) e quelle per eseguire prodotti e quozienti;

• nel caso di serie di funzioni, stabilire quando sia possibile generalizzare a somme infinite i teoremi classici dell’analisi su limiti, derivate e integrali di somme.