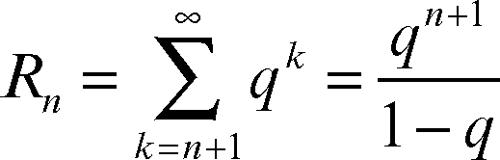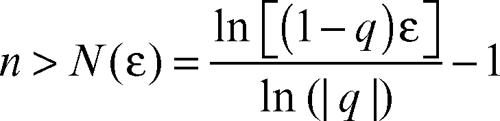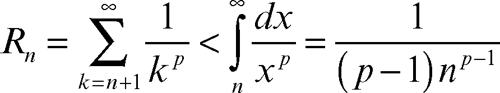serie numerica, velocita di convergenza di una

serie numerica, velocita di convergenza di una

serie numerica, velocità di convergenza di una informalmente, numero di termini di una serie convergente che occorre considerare per avere una buona approssimazione della sua somma finita. Una serie numerica convergente è, infatti, una scrittura additiva infinita del numero reale a cui essa converge; scrivere una serie numerica significa indicare, quindi, un metodo di approssimazione di tale numero reale. Tuttavia è necessario, per le applicazioni pratiche, che la sua convergenza non sia troppo lenta, cioè che non si debbano calcolare troppi termini per ottenere l’approssimazione richiesta. Se la serie

ha somma S, limite della successione {s_n} delle sue somme parziali, allora, fissato un errore ε > 0, esiste un valore N = N(ε) tale che il modulo del resto |R_n| = |S − s_n| risulti, ∀n > N, minore di ε. Se la serie non si riduce a una somma finita, risulta

e l’ordine di questo infinito dà una stima della lentezza della convergenza. Infatti, quanto minore è N a parità di ε, tanto minore è il numero di addendi che debbono essere addizionati per ottenere il risultato con la precisione voluta. Per esempio, la serie geometrica di ragione q, con |q| < 1, ha resto

Pertanto |R_n| < ε se

Questa funzione cresce con |q|, mostrando che la convergenza di una serie geometrica è tanto più rapida quanto più la sua ragione è prossima a 0. La rapidità di convergenza di una serie che soddisfa il criterio del rapporto o della radice con limite l è paragonabile a quella di una serie geometrica di ragione q = l. Le serie per cui l = 0 sono rapidamente convergenti: per esempio, il resto della serie fattoriale è minore di

Invece, le serie per cui questi criteri falliscono, come le serie armoniche generalizzate con esponente p > 1, pur se convergenti, hanno velocità di convergenza tanto minore quanto minore è p. Infatti il resto della serie

è

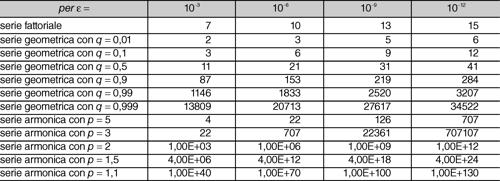
per cui N(ε) = [(p − 1)ε]^−1/(p−1). I valori di N(ε) per alcune di queste serie, al variare di ε da 10⁻³ a 10⁻¹², sono riportati in tabella. Dai valori in tabella si evince come serie dichiarate più rapidamente convergenti di altre possono non sembrare tali finché l’errore è abbastanza piccolo. Nei casi in cui la convergenza è lenta è possibile cercare di accelerarla sottraendo da essa una serie avente la stessa velocità di convergenza, ma di somma nota (→ Mengoli, serie di); per questo si parla di accelerazione di convergenza di una serie numerica.

Le serie convergenti semplicemente ma non assolutamente hanno velocità di convergenza bassa: per esempio, la serie armonica a segni alterni converge con la rapidità della serie di Mengoli.

Anche per serie di funzioni, come le serie di Fourier, è possibile accelerare la convergenza mediante opportuni accorgimenti, come l’uso di metodi alternativi di sommazione (in particolare il metodo di Cesàro; si veda → sommazione, metodi di).