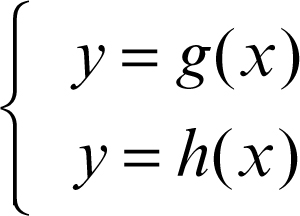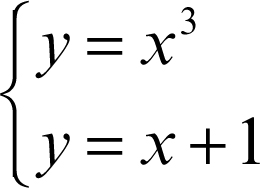soluzioni, separazione delle

soluzioni, separazione delle

soluzioni, separazione delle metodo per determinare un intervallo chiuso [a, b] in cui l’equazione ƒ(x) = 0 ha una e una sola soluzione; il metodo viene utilizzato nella ricerca delle soluzioni approssimate di un’equazione con un metodo numerico (→ approssimazione (di una soluzione)). Poiché risolvere l’equazione ƒ(x) = 0 equivale a cercare gli zeri della corrispondente funzione y = ƒ(x), il metodo si sviluppa in due fasi: a) la determinazione degli intervalli del dominio di ƒ in corrispondenza dei quali vi è uno e un solo zero; b) la ricerca all’interno di tali intervalli del corrispondente zero della funzione, cioè di una soluzione dell’equazione ƒ(x) = 0. Per questo si utilizzano alcuni teoremi:

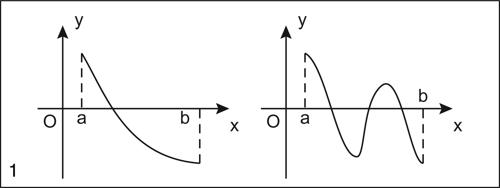
• il teorema di esistenza degli → zeri di una funzione che stabilisce che se la funzione ƒ è continua nell’intervallo [a, b] e assume negli estremi valori di segno opposto, cioè ƒ(a) ⋅ ƒ(b) < 0, allora esiste almeno uno zero all’interno dell’intervallo considerato. È possibile che ce ne sia più di uno, e comunque ne esiste sicuramente un numero dispari: la tesi del teorema fornisce pertanto solo una condizione sufficiente ma non necessaria per l’esistenza degli zeri;

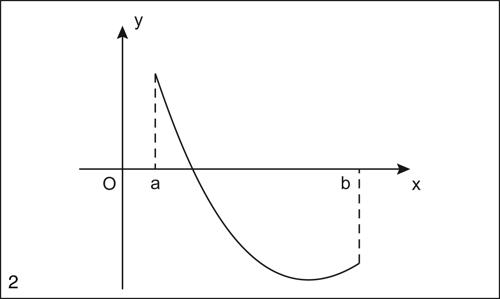
• i due teoremi di unicità della soluzione: il primo afferma che, verificate le ipotesi del teorema di esistenza degli zeri, se y = ƒ(x) è derivabile una volta in (a, b) e se ƒ′ mantiene lo stesso segno nell’intervallo, allora esiste una e una sola soluzione in (a, b). Il secondo teorema generalizza il risultato, basandosi sulla costanza di segno della derivata seconda, ed estende l’ipotesi restrittiva del primo teorema relativa alla necessità del carattere monotono di ƒ(x): se y = ƒ(x) è derivabile due volte e ƒ″ (x) mantiene lo stesso segno in (a, b), allora esiste una e una sola soluzione in (a, b).

Accertate le ipotesi del teorema di esistenza e dei teoremi di unicità della soluzione, si possono utilizzare i metodi numerici più opportuni per approssimare gli zeri, come il metodo di → bisezione, il metodo delle → secanti, il metodo di → Newton, il metodo dell’→ attrattore.

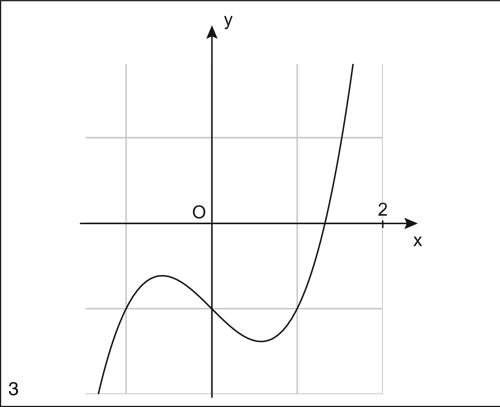
Per esempio, si consideri l’equazione x ³ − x − 1 = 0; la funzione y = ƒ(x) = x ³ − x − 1 ha nell’intervallo [0, 2] almeno uno zero perché ƒ è continua e ƒ(0) = −1 e ƒ(2) = 5; quindi i valori della funzione cambiano di segno agli estremi dell’intervallo considerato (teorema di esistenza degli zeri); inoltre la derivata prima si annulla in

e il valore +0,58 cade all’interno dell’intervallo [0, 2]; quindi non è applicabile il primo teorema sull’unicità; la derivata seconda ƒ″ (x) = 6x è però sempre positiva in [0, 2] e soddisfa le ipotesi del secondo teorema di unicità. Ne consegue che esiste uno e un solo zero della funzione nell’intervallo considerato e l’equazione ha una (e una sola) soluzione in [0, 2].

I due teoremi sull’unicità della soluzione sono utili quando i calcoli delle derivate prime e seconde e del loro segno sono semplici; questo è il caso, per esempio, delle funzioni polinomiali. Nel caso di funzioni algebriche più complesse o di funzioni trascendenti, il calcolo delle derivate e lo studio del loro segno può comportare invece difficoltà: si può allora ricorrere a opportune trasformazioni della funzione e alla sua rappresentazione grafica. Se è possibile riscrivere la funzione y = ƒ(x) come differenza di due funzioni ƒ(x) = g(x) − h(x), allora ƒ(x) = 0 ⇔ g(x) = h(x). Questa equazione può essere interpretata come l’equazione risolvente del sistema:

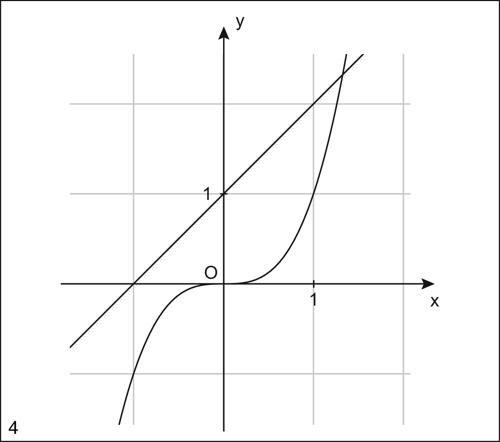
Risolvere il sistema vuol dire ricercare le intersezioni tra le due curve che sono i rispettivi grafici delle due funzioni; le ascisse dei punti di intersezione danno le soluzioni dell’equazione ƒ(x) = 0. È così possibile determinare, almeno approssimativamente, gli intervalli in cui tali soluzioni sono comprese. Il metodo è di facile applicazione quando una delle due funzioni g(x) o h(x) è lineare; in questo caso si tratterà di determinare le intersezioni tra una retta e una curva. Nel caso della funzione dell’esempio precedente, una volta stabilita l’esistenza e l’unicità della soluzione in [0, 2], si può riscrivere in modo equivalente l’equazione y = ƒ(x) = x ³ − x − 1 come x ³ = x + 1, che è l’equazione risolvente del sistema:

Si tratta allora di determinare approssimativamente le ascisse dei punti di intersezione tra la cubica y = x ³ e la retta y = x + 1. La rappresentazione grafica conferma che nell’intervallo [0, 2] è compresa l’ascissa del punto di intersezione della cubica con la retta; questa è la soluzione dell’equazione x ³ − x − 1 = 0.