Scienza greco-romana. Le sfere celesti e le origini della trigonometria
Scienza greco-romana. Le sfere celesti e le origini della trigonometria
Le sfere celesti e le origini della trigonometria
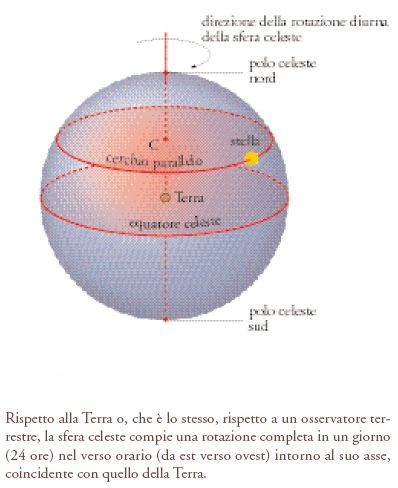
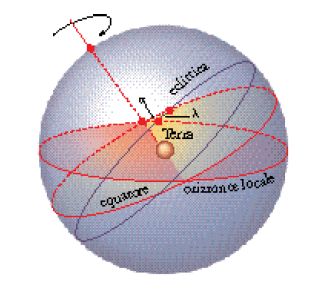
La comparsa della sfera nella geometria è una diretta conseguenza del fatto che il modello greco del Cosmo e del posto occupato in esso dalla Terra è costituito da due sfere concentriche: un’immensa sfera esterna che delimita il Cosmo e sulla cui superficie si trovano le stelle fisse, e una sfera concentrica, la Terra, talmente piccola rispetto alla prima da potersi considerare un punto (fig. 1). La sfera esterna, quella delle stelle fisse, ruota da oriente a occidente con moto giornaliero, trasportando le stelle situate sulla sua superficie. Queste, con la loro rotazione, descrivono ogni giorno dei cerchi paralleli il cui centro (C per la generica stella indicata nella figura) si trova sull’asse di rotazione che interseca la sfera nei due ‘poli celesti’, nord e sud; perpendicolare a tale asse, attraverso il centro della Terra, è il piano che determina sulla sfera il ‘cerchio massimo’ (mégistos kýklos) denominato ‘equatore celeste’.
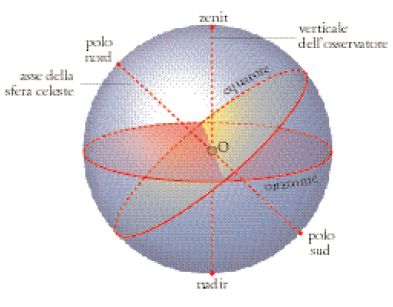
Poiché osservatori collocati in punti diversi della Terra vedono differentemente la sfera esterna, si pone l’esigenza di spiegare una serie di fenomeni astronomici locali: trovare, per esempio, quante ore di luce vi saranno in un dato giorno; quale fra due stelle date sorge o tramonta prima; il periodo di tempo durante il quale una stella è resa invisibile dalla luce del Sole; l’angolo che si forma tra alcuni cerchi massimi. Problemi di questo tipo implicano la considerazione dell’‘orizzonte’ di un osservatore, cioè di quel cerchio massimo definito dal piano passante per il centro della Terra e perpendicolare alla linea, detta ‘verticale locale’, che unisce il punto sulla sfera celeste direttamente sopra la testa dell’osservatore (che sarà chiamato successivamente ‘zenit’) e il centro della Terra (il punto della sfera celeste opposto ad esso rispetto all’osservatore o, se si vuole, rispetto al centro della Terra, sarà chiamato ‘nadir’): v. fig. 2 (in questa, il cerchio che appare verticale è la sezione della sfera con il ‘piano meridiano’ dell’osservatore, cioè con il piano contenente i due poli e l’osservatore). Il ruolo svolto dall’orizzonte in problemi di questo tipo appare immediatamente evidente quando si pensa che è la posizione dell’orizzonte a determinare quali stelle fisse siano visibili (in quanto si trovino sopra l’orizzonte dell’osservatore) e per quanto tempo.
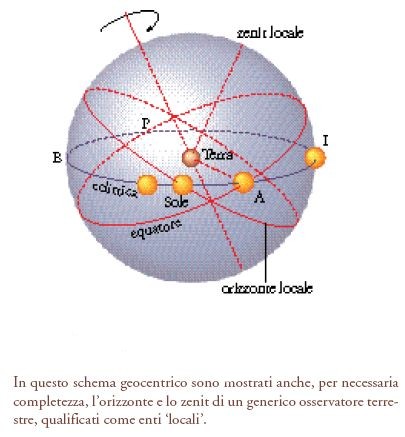
I fenomeni connessi alle stelle fisse interagiscono poi con quelli associati al Sole, come le diverse apparizioni del cielo notturno e il variare della lunghezza della luminosità diurna durante le stagioni. A governare tali fenomeni è la posizione del Sole sul cerchio massimo (l’‘eclittica’) che ne rivela il passaggio annuale attraverso i segni dello Zodiaco; Autolico di Pitane ed Euclide lo chiamano «il cerchio dei segni», Tolomeo lo chiama «il cerchio che attraversa i segni» e nessuno di loro usa il termine greco corrispondente a ‘eclittica’. Poiché il cerchio dell’eclittica è inclinato rispetto all’equatore (fig. 3), la distanza angolare δ del Sole dall’equatore – ciò che si chiama la ‘declinazione’ del Sole – varia durante il corso dell’anno: ai due equinozi, di primavera (P) e d’autunno (A), il Sole si trova sull’equatore, al solstizio d’estate (E) è alla massima distanza (δ=+23°27´) a nord dall’equatore e nel giorno del solstizio d’inverno (I ) si trova alla stessa distanza a sud da esso (δ=-23°27´). Il cerchio dell’eclittica costituisce un elemento di complicazione che va ad arricchire la configurazione geometrica studiata nell’antica scienza della sfera – chiamata dai Greci ‘sferica’ – che aveva come oggetto proprio lo studio di questa configurazione di cerchi: l’eclittica, l’orizzonte, l’equatore e i cerchi paralleli.
Dal momento che i problemi matematici della sferica sono così strettamente collegati a quelli astronomici, si userà il termine ‘sferica’ per denotare non soltanto un corpo di teoremi sulla geometria della superficie sferica, ma anche tutte quelle proposizioni astronomiche nei trattati greci che possono aver motivato o fornito applicazioni per questi teoremi. La parte della scienza della sfera sviluppata in trattati dal titolo Sphaerica (che potrebbe tradursi con ‘Sferici’ intendendo ‘cose sferiche’) rappresenta soltanto uno degli antichi approcci allo studio di tali problemi: sarà dunque utile prendere in considerazione anche tutti gli altri.
Le prime opere
Eudosso e gli inizi della scienza della sfera
Il trattamento matematico dei problemi derivanti dal modello sferico del Cosmo sembra risalire almeno ai tempi di Platone. Nel Libro VII della Repubblica di Platone, Socrate avverte gli allievi di non occuparsi di ciò che sta in cielo materialmente; ciò è senza dubbio in accordo con i Phaenomena di Eudosso di Cnido (attivo nella prima metà del IV sec. a.C.), un’antica opera greca sulla scienza della sfera che descrive le apparizioni celesti (phainómena) all’interno del modello a due sfere (l’opera è andata perduta, fu però messa in versi da Arato di Soli e oggetto di un commentario critico da parte di Ipparco di Nicea).
Successive all’opera di Eudosso vi sono tre opere scritte secondo il diverso stile deduttivo della matematica classica greca: il De sphaera quae movetur (Sulla sfera mobile) e il De ortibus et occasibus (Albe e tramonti) di Autolico di Pitane e i Phaenomena di Euclide. Autolico si può collocare con certezza nell’ultimo terzo del IV sec. a.C., mentre Euclide è ritenuto di poco posteriore. Le opere di questi due autori presentano scopi e metodi simili e aprono due finestre sullo stato della teoria, in particolare su quelli che erano i suoi presupposti astronomici e geometrici; essi citano infatti alcuni teoremi non banali di sferica, i quali non possono che essere stati tratti da autori precedenti, e inducono a credere che una seria indagine sulla teoria della sfera abbia avuto inizio almeno a partire dalla metà del IV secolo.
Sicuramente, dato che una parte così consistente della teoria è originata da problemi di astronomia sferica, lo sviluppo della matematica presente in questi trattati è da collocarsi successivamente al periodo in cui i Greci cominciarono a derivare spiegazioni e predizioni dei fenomeni celesti dal modello a due sfere del Cosmo. Tale modello era noto a Eudosso, l’autore dei perduti già ricordati Phaenomena, anche se ci sono ben pochi elementi per sostenere che egli sia stato l’autore di ciò che si è finito col chiamare ‘sferica preeuclidea’. Quello che si può dire è che tale teoria, la cui ricostruzione è stata tentata all’inizio del XX secolo, fu sviluppata probabilmente durante quella metà di secolo che approssimativamente separa lo scritto di Eudosso da quelli di Autolico.
Le opere di Autolico
Sia il De ortibus et occasibus che il De sphaera quae movetur sono stati pubblicati in greco. È stato dimostrato (Schmidt 1952) che i due libri del De ortibus di Autolico di Pitane sono di fatto soltanto due versioni di una stessa opera dedicata alle cosiddette fasi delle stelle, un’antica topica dell’astronomia greca. Si tratta del succedersi apparente, nel corso di un anno, di otto fasi di una stella fissa che dipendono dalla posizione occupata dalla stella rispetto all’eclittica. Le prime quattro fasi sono la levata ‘eliaca’ o il tramonto ‘eliaco’ della stella, cioè contemporanei con il levare del Sole, e la levata o il tramonto ‘acronittici’ o ‘serali’, cioè contemporanei al tramonto del Sole, ‘veri’, mentre le seconde quattro sono la levata o il tramonto eliaci o serali ‘apparenti’ della stella, cioè quando la levata o il tramonto della stella sono ‘visti’ la prima volta prima del sorgere del Sole (eliaci) o dopo il suo tramonto (serali).
La libera utilizzazione da parte di Autolico della terminologia tecnica dell’astronomia mostra come il suo non fosse un trattato destinato ai principianti. I risultati sono a volte semplicemente descrittivi, nella maggior parte dei casi sono qualitativi, ma mai quantitativi (per es., nel De ortibus, I, 1 si stabilisce che le levate o i tramonti eliaci apparenti di una stella fissa seguono quelli veri, mentre per quanto riguarda le levate o i tramonti serali veri e apparenti si verifica esattamente il contrario). Un esempio del livello di conoscenze matematiche presupposte nel trattato è dato dalla costruzione di cerchi massimi tangenti a cerchi minori. Inoltre, in tutta l’opera, Autolico dà per scontato che il lettore conosca quali tra i circoli astronomici utilizzati sono cerchi massimi e sappia che i cerchi massimi si bisecano reciprocamente.
Come il De ortibus, anche il De sphaera quae movetur si apre con alcune definizioni e con un lemma relativo a un punto che si muove uniformemente; non si fa riferimento né al Sole né alle stelle ma semplicemente a punti che sono trasportati dalla rotazione uniforme della sfera, dando luogo in tal modo a un sistema di cerchi paralleli e di archi simili (teoremi 1-3). Autolico si serve anche del piano dell’orizzonte che separa l’emisfero visibile da quello invisibile, e introduce gli importanti casi relativi a un osservatore posto all’equatore (la sphaera recta degli astronomi latini) o in qualsiasi punto che non sia l’equatore o il polo (sphaera obliqua; dove le parole ‘retto’ e ‘obliquo’ si riferiscono all’angolo formato dall’orizzonte con l’equatore). Nei teoremi 7-11 l’autore tratta questo secondo caso e fornisce, tra le altre cose, un paragone qualitativo relativo al tramonto/levata di due punti che sorgono/tramontano contemporaneamente e mostra che durante una rotazione della sfera un cerchio che passa per i poli si trova a essere per due volte perpendicolare all’orizzonte. L’opera termina con un teorema, il 12, che fornisce una condizione sufficiente affinché un cerchio su una sfera sia un cerchio massimo.
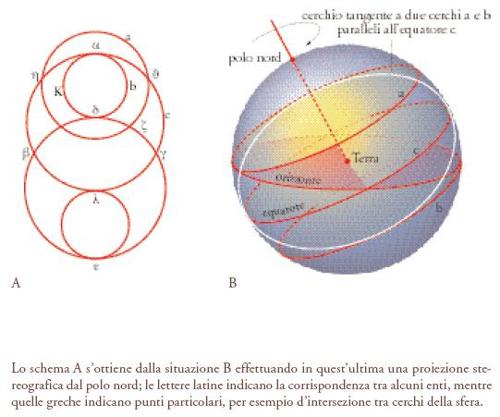
Un aspetto che colpisce nei manoscritti delle opere di Autolico è il metodo per rappresentare configurazioni di cerchi che differisce molto dai metodi moderni. A titolo di esempio e di comparazione a questo riguardo, la fig. 4 riporta il diagramma originale e un’interpretazione in termini moderni di uno schema grafico del De sphaera quae movetur relativo ad alcuni cerchi notevoli sulla sfera terrestre, già nominati sopra.
I Phaenomena di Euclide
Quest’opera appartiene allo stesso genere delle opere di Autolico ma è mirata alla derivazione di risultati qualitativi relativi ai tempi di levata di archi dell’eclittica. Il ‘tempo di levata’ di un arco l dell’eclittica (fig. 5) è il tempo impiegato dall’arco per sollevarsi sopra l’orizzonte di una località ed è misurato di norma in ‘gradi di tempo’, cioè come ampiezza in gradi di quell’arco a dell’equatore che attraversa l’orizzonte insieme all’arco l di eclittica considerato. Poiché l’equatore è perpendicolare all’asse della rotazione giornaliera, esso mantiene un angolo costante con l’orizzonte quando quest’ultimo ruota e perciò si solleva alla velocità uniforme di 1° ogni quattro minuti (pari a 360° in 24 ore).
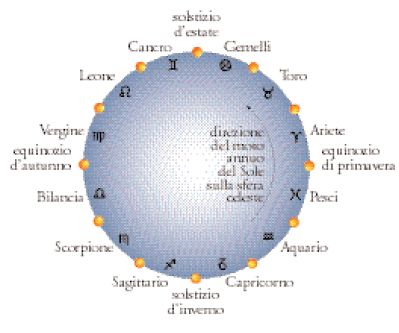
Il testo esistente dei Phaenomena è preceduto da un’introduzione in cui si avanzano, sulla base dei fenomeni osservati, quattro postulati concernenti aspetti del modello a due sfere, il primo dei quali afferma che le stelle si muovono descrivendo cerchi. Sono in seguito definiti i principali cerchi celesti (compresi il ‘tropico settentrionale’ e il ‘tropico meridionale’: oggi, rispettivamente, Tropico del Cancro e Tropico del Capricorno) ed è indicato che l’orizzonte, l’equatore e l’eclittica sono cerchi massimi. Il trattato vero e proprio si apre con due teoremi: il primo afferma che la Terra si trova al centro del Cosmo e il secondo stabilisce quante volte, durante una rotazione della sfera celeste, vari cerchi massimi si trovano a essere perpendicolari l’uno all’altro. Seguono quindi quattro teoremi (3-6) sulle posizioni e sulla successione apparente delle levate e dei tramonti delle stelle fisse, e poi sette teoremi (7-13) sui luoghi e sui tempi delle levate e dei tramonti dei segni zodiacali (la fig. 6 mostra l’ordine di questi segni quando l’eclittica è vista dal polo nord). Gli ultimi due teoremi di questo gruppo confrontano, rispettivamente, i tempi di tramonto dei segni compresi nel semicerchio dell’eclittica che segue il Cancro (in senso antiorario) con i tempi di levata dei segni compresi nel semicerchio che segue il Capricorno. I teoremi conclusivi (14-18) confrontano i tempi che impiegano archi di eclittica uguali ad ‘attraversare’ l’emisfero visibile e quello invisibile.
Nei teoremi 12 e 13 colpisce la presenza di una certa asimmetria nei risultati relativi alle levate e ai tramonti, perché Euclide non dice nulla né sui tempi di levata degli archi compresi nel semicerchio che segue il Cancro, né sui tempi di tramonto nel semicerchio che segue il Capricorno. Tuttavia, utilizzando semplicemente una tavola dei tempi di levata – quale può essere quella contenuta in Almagesto, II, 8 – diventa evidente che Euclide non potesse dire nulla su tali tempi utilizzando le stesse semplici argomentazioni con cui aveva ottenuto gli altri risultati; in un certo senso, si può dire che egli abbia assunto i metodi qualitativi tipici di questi trattati fin dove essi funzionavano.
Autolico ha utilizzato un linguaggio più geometrico di quello di Euclide, ma la somiglianza della struttura delle dimostrazioni dei teoremi dei suoi trattati con quella presente negli Elementi sta a dimostrare come, a prescindere da quante nozioni fisiche fossero coinvolte, la tradizione all’interno della quale entrambi gli autori scrivevano fosse quella del trattamento matematico dei loro argomenti. Infine, l’incompletezza formale di questi trattati, i quali in maniera piuttosto casuale citano dei risultati utilizzandoli come se si trattasse di dati ben noti, è prova del fatto che essi sono soltanto parti di un progetto più ampio; sia Autolico sia Euclide, infatti, stavano lavorando evidentemente in un contesto di problemi, di risultati e di metodi che erano familiari, non soltanto nell’area specifica della sferica ma, in generale, nell’area della geometria solida. Nessuno dei due scriveva per principianti.
I contributi di Ipparco
Con l’opera di Ipparco di Nicea, verso la metà del II sec. a.C. fecero la loro comparsa alcuni metodi per affrontare i problemi relativi alla sfera che consentivano di trattare numericamente problemi fino a quel momento trattati soltanto qualitativamente. I due eventi più significativi di questo sviluppo furono, da un lato, l’introduzione nel mondo greco della divisione sessagesimale babilonese del cerchio in 360 gradi (simbolo: °) – ognuno dei quali diviso in 60 primi (simbolo: ') di 60 secondi (simbolo: ") l’uno –, unitamente all’aritmetica del sistema sessagesimale; dall’altro lato il calcolo di Ipparco di una tavola delle corde in un cerchio, che fornisce le lunghezze delle corde che sottendono una successione di archi in un cerchio di raggio fissato. Una tavola siffatta può essere utilizzata per gli stessi scopi di una tavola dei seni e rende possibile per la prima volta dare risposte quantitative precise a problemi di sferica.
Anche se la tavola delle corde di Ipparco non ci è pervenuta, si tende ad accettare l’opinione di Neugebauer secondo cui gli argomenti della tavola progredivano per intervalli di 7,5° ed è conosciuta un’antica tavola indiana di corde che sottendono archi separati tra loro da questo stesso intervallo. Una tavola siffatta avrebbe potuto essere prodotta con metodi che richiedevano una conoscenza geometrica appena superiore al teorema di Pitagora e ad altri risultati altrettanto elementari, e con l’ausilio di una conoscenza aritmetica sufficiente a calcolare le radici quadrate, come aveva fatto Archimede un secolo prima di Ipparco.
Sulla base di una testimonianza alquanto vaga di Sinesio di Cirene (370 ca.-413) a Ipparco è stata anche attribuita la scoperta del modo attraverso cui rappresentare la superficie della sfera sul piano dell’equatore mediante una proiezione (stereografica) dal polo sud della sfera. Che si accetti o no questa notizia, si ha una chiara testimonianza del fatto che questo importante metodo geometrico esisteva all’epoca di Vitruvio poiché tra i vari orologi che indicano il sorgere degli astri descritti nella sua opera ve n’è uno basato sulla proiezione stereografica. Di Ipparco ci sono pervenuti inoltre i titoli di due opere, il Trattato sulle levate simultanee e Sulle ascensioni dei dodici segni zodiacali, che, combinati con l’informazione fornita da Pappo, fanno pensare che l’autore avesse risolto il problema lasciato insoluto da Euclide nella proposizione 12 dei Phaenomena, vale a dire quello relativo ai tempi di levata per i segni situati nella metà dell’eclittica compresa tra il Cancro e il Sagittario. In effetti – secondo quanto dice Pappo (Collectio mathematica, VI, 55) – Ipparco mostrò come lo schema di Euclide portasse a un tipo di asserzioni sui tempi di levata non vero per il semicerchio che segue il Cancro. Pappo testimonia infatti che Ipparco dimostrò «per mezzo dei numeri» che per certe regioni un arco nel semicerchio dell’eclittica dal Cancro al Sagittario vicino all’equinozio si solleverà in un tempo più lungo di quello impiegato da un arco uguale vicino al solstizio; generalmente si assume che la formula «per mezzo dei numeri» stia a significare «per mezzo di metodi numerici», quali potevano essere le progressioni aritmetiche usate dai Babilonesi o gli stessi metodi trigonometrici di Ipparco.
L’Anaphoricus di Ipsicle e i trattati di Teodosio
Sappiamo con sicurezza, in quanto ci è pervenuto il suo trattato Anaphoricus (Sulle ascensioni), che metodi numerici furono usati da Ipsicle, contemporaneo di Ipparco. Per il periodo immediatamente successivo, Strabone (Geographica, XII, 4, 9) elenca come uno tra i più illustri matematici Teodosio di Bitinia, che perciò si ritiene sia vissuto poco dopo Ipparco, probabilmente attorno alla fine del II sec. a.C. Tra i suoi trattati che ci sono pervenuti vi sono il De diebus et noctibus (in due libri), il De habitationibus e gli Sphaerica; i primi due presentano lo stesso stile generale dei trattati già discussi di Autolico e di Euclide, mentre gli Sphaerica sono il primo trattato, tra quelli ancora esistenti, dedicato alla sferica intesa come topica matematica.
Teodosio, in effetti, elimina interamente dal suo trattato tutto ciò che ha a che fare con il mondo fisico e con il movimento in particolare, al punto che se Euclide nei suoi Elementi aveva definito la sfera nei termini della rotazione di un semicerchio attorno al suo diametro, egli la definisce invece in maniera completamente geometrica, analogamente a quanto fatto da Euclide per il cerchio, come il solido contenuto da una superficie tale che tutti i punti di essa sono equidistanti da un punto dato. La forma astratta nella quale sono date le proposizioni ha reso matematicamente poco intuitivo il contenuto del trattato. Questo è evidente, per esempio, nel passo in cui Teodosio assume che un punto d’intersezione di due cerchi massimi – in un contesto astronomico, l’equatore e l’eclittica – sia un polo di un terzo cerchio massimo – l’orizzonte di quel punto (Sphaerica, III, prop. 5). Di fatto non è difficile mostrare che la prima assunzione di Teodosio circa il fatto che il polo dell’equatore si trovi su un orizzonte renda superflua l’assunzione supplementare. La stessa considerazione vale per un caso analogo (ibidem, prop. 6) anche se qui sembra che per avere una dimostrazione semplice sia necessario un teorema di congruenza per i triangoli sferici come quello dato in materia da Menelao di Alessandria (Sphaerica, I, prop. 12) e di cui presumibilmente Teodosio non disponeva. Pappo, il quale non si accorse dell’assunzione superflua per la proposizione 5 del Libro III, la notò invece nel caso della proposizione 6; tuttavia, egli si servì di nove teoremi preliminari (12-20) per mostrare che l’assunzione non era necessaria, quando gli sarebbero bastate poche linee se avesse fatto riferimento agli Sphaerica di Menelao.
La storiografia della scienza ha discusso i punti in cui si corrispondono il trattamento della geometria della sfera nel Libro I di Sphaerica di Teodosio e quello del cerchio in Elementi di Euclide (Heath 1921) nonché altre corrispondenze degli Elementi con il detto Libro I di Sphaerica (Björnbo 1902). Queste corrispondenze, per quanto corrette, sono tuttavia fuorvianti se le si pensa in relazione alla motivazione complessiva dei testi; concetti come quello di ‘cerchio parallelo’ e di ‘polo di un cerchio’, per quanto possano essere analoghi alle idee di corde di un cerchio e di estremità di un diametro che biseca questa corda, sono in realtà fondamentali per l’astronomia sferica e la loro introduzione può essere vista in quella luce. Così, i teoremi 11-12 nel Libro I sui cerchi massimi che si bisecano reciprocamente, nonostante corrispondano ai teoremi euclidei sulle corde che si bisecano vicendevolmente, risultano anche fondamentali per l’astronomia sferica. Un altro importante gruppo di teoremi per l’astronomia sferica è rappresentato dai teoremi 13- 15, i quali mostrano che se G è un cerchio massimo e S è un cerchio minore sulla sfera, allora sono equivalenti i seguenti asserti: (1) G biseca S, (2) G è perpendicolare a S e (3) G contiene i poli di S. Il teorema 15 è usato spesso da Autolico, mentre il 13 e il 15 sono entrambi utilizzati nel teorema 2 dei Phaenomena di Euclide; tuttavia, come si vedrà, Teodosio e Autolico usano i teoremi 13 e 15 in maniera molto diversa. Per quanto riguarda gli altri teoremi e le altre costruzioni del Libro I, va ricordato che Teodosio non chiarisce mai se, per i problemi che risolve, l’interno della sfera si debba o meno considerare accessibile; nel primo caso certi problemi diventano banali, nel secondo caso, altri problemi non sono risolvibili utilizzando i suoi metodi.
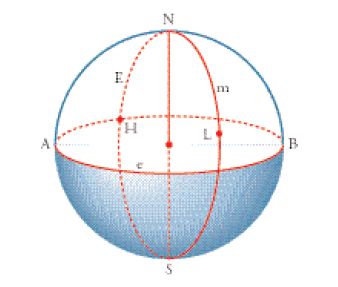
Il Libro II si apre con una definizione dei cerchi tangenti su una sfera e, per i teoremi introduttivi, è possibile sottolineare ancora una volta le analogie con i teoremi degli Elementi, per quanto la connessione con l’astronomia motivi sufficientemente i primi dieci teoremi di questo libro relativi ai cerchi massimi, ai cerchi paralleli e ai loro cerchi tangenti. Per la parte del Libro II successiva al teorema 10 si possono sottolineare le applicazioni all’astronomia. Per esempio, nella dimostrazione del già discusso teorema 13 Teodosio introduce la nozione di «semicerchi che non s’incontrano » o «semicerchi asintotici» (asýmptōta hēmikýklia), che sono semicerchi massimi su una sfera che non incontrano determinati altri semicerchi massimi; per esempio, nella fig. 7 il semicerchio massimo AHB dell’equatore e è asintotico rispetto al semicerchio NLS del cerchio meridiano m di un luogo L, cioè passante per L e per i poli celesti N e S. La nozione di tali semicerchi compare nei Phaenomena (teoremi 4-7, 12 e 14), dove è utilizzata per dimostrare che certi archi sono uguali, nonché nel De sphaera di Autolico (teorema 8).
Il gruppo dei teoremi 13-15 del Libro II dimostra, dal modo in cui sono utilizzati i teoremi 13 e 15 del Libro I nella dimostrazione del teorema 13 del Libro II, che la teoria dei cerchi tangenti sulla sfera ha subito un mutamento fra Euclide e Teodosio. Il teorema 15 del Libro I, per esempio, costituiva parte dell’antica teoria delle tangenti, ma qualcuno dopo Autolico lo applicò per stabilire una nuova teoria delle tangenti; inoltre, il teorema 15 del Libro II esibisce la costruzione di un cerchio massimo tangente a un cerchio parallelo e passante per un dato punto compreso tra quest’ultimo cerchio e l’altro cerchio parallelo uguale a esso. Anche se la dimostrazione fa uso della teoria della tangenza di Teodosio, Euclide, nei Phaenomena, si appella a questo teorema per le dimostrazioni dei teoremi 4, 5 e 12 e anche Autolico lo cita parola per parola. Sembra perciò che i risultati dei teoremi 13-16 siano parte di un capitolo preeuclideo dell’argomento, posti però su una base differente da uno scrittore successivo.
Sempre nel Libro II, un’altra prova del progresso avutosi nel trattamento della sferica nel periodo tra Euclide e Teodosio è contenuta nel sofisticato trattamento dell’angolo d’inclinazione tra due cerchi massimi, esposto nel teorema 22. L’uso da parte di Teodosio dell’altezza del polo di un cerchio su un altro per studiare la variazione monotona dell’angolo tra i cerchi da un massimo a un minimo, unitamente alla sua discussione delle simmetrie, va ben al di là del trattamento di questa topica dato da Euclide (Phaenomena, prop. 2). Teodosio, tuttavia, misura l’altezza del polo di un cerchio sull’altro non con l’arco del cerchio massimo che congiunge i poli, ma con la linea retta perpendicolare dal polo di un cerchio al piano dell’altro cerchio; in generale, egli non ha raggiunto quella facilità nel trattamento degli angoli conseguita da Menelao.
L’Introduzione ai fenomeni di Gemino
Nel secolo successivo a Ipparco, Ipsicle e Teodosio, si ha l’Introduzione ai fenomeni di Gemino (attivo verso il 70 a.C.), un compendio nel quale l’autore ha incorporato gran parte del materiale precedente relativo al modello a due sfere con il suo asse e i suoi poli (cap. 4). Gemino discute i diversi cerchi massimi e cerchi paralleli importanti, il variare della lunghezza del giorno e della notte secondo le stagioni e la latitudine geografica (cap. 6) e le fasi delle stelle. Si tratta del primo resoconto della materia pervenutoci in forma di compendio, una forma destinata a divenire predominante nella tradizione scientifica romana.
Gli ‘Sphaerica’ di Menelao
L’opera di Menelao di Alessandria (Sphaerica, in tre libri) – sulla base di due osservazioni riportate da Tolomeo in Almagesto, III, 7, 3 – può essere datata intorno al 100 d.C., cioè quando era già nato Tolomeo e due secoli e mezzo dopo l’opera di Teodosio. Anche se il testo greco non ci è pervenuto, l’opera sopravvive nell’edizione araba di Ibn 'Irāq, Abū Naṣr Manṣūr ibn 'Alī, e in una traduzione latina dall’arabo di Gherardo da Cremona. Per un curioso destino, non raro nella storia della matematica, Menelao è rimasto famoso per un teorema che era senza dubbio noto prima di lui, mentre i suoi più importanti, e certamente personali, contributi alla sferica sono meno conosciuti.
Nella prefazione agli Sphaerica, Menelao afferma di avere messo in risalto i contributi dei suoi predecessori ogniqualvolta questi erano nel giusto, di avere generalizzato molti fatti che erano stati dimostrati per casi singoli e di essersi impegnato a evitare la reductio ad absurdum nelle dimostrazioni. A parte una o due eccezioni estremamente interessanti, che saranno discusse più avanti, l’opera tratta esclusivamente dei cerchi massimi e del trilatero. Essa presenta un interesse geometrico generale, indipendentemente da ogni applicazione astronomica, e costituisce una teoria i cui elementi verranno molto più tardi riconosciuti come parte dello studio della geometria non euclidea. È anche la prima opera in cui svolgono un importante ruolo gli angoli sulla sfera. Considerati i riferimenti ai suoi predecessori e a quanti hanno già scritto sugli elementi della sferica, è difficile stabilire con certezza se un certo particolare concetto o teorema sia o no un contributo di Menelao, sicché si rimarrà su un terreno più sicuro interpretando il suo trattato come il migliore sviluppo di una disciplina con una lunga storia che un matematico esperto poteva mettere insieme alla fine del I secolo.
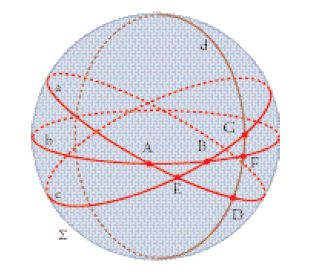
Senza dubbio Menelao fu un astronomo ed è certo che egli fu consapevole delle applicazioni astronomiche della teoria che esponeva. Nella prefazione riferisce di avere applicato egli stesso le sue idee a problemi astronomici e, a conferma di ciò, Pappo gli attribuisce un’opera che affronta problemi nei tempi di levata e di tramonto che Euclide non avrebbe potuto affrontare nei suoi Phaenomena. Menelao dà per scontato che il lettore conosca le nozioni fondamentali della sferica (cerchi massimi, poli, ecc.) e una serie di conoscenze avanzate in quest’ambito. Il Libro I degli Sphaerica si apre con tre definizioni, la prima delle quali introduce il ‘trilatero’ – termine che Pappo (Collectio mathematica, VI, teorema 1) attribuisce a Menelao – come una figura sferica a tre lati, ciascuno dei quali costituito da un arco di cerchio massimo minore di un semicerchio (senza una simile restrizione sulla grandezza dei lati un quadrante di una sfera potrebbe essere un trilatero); nella fig. 8 sono riconoscibili vari trilateri, quali ABE e BGF (che sono opposti al vertice comune B), AFD e altri, derivanti dall’intersezione dei quattro cerchi massimi a, b, c, d della sfera Σ. Successivamente Menelao introduce gli angoli di un trilatero come gli angoli formati dai piani dei cerchi massimi che formano i suoi lati e stabilisce che questi angoli siano misurati confrontando gli archi risultanti sul cerchio massimo che unisce i poli dei cerchi massimi che costituiscono i lati degli angoli.
Il Libro I sembra scritto con l’intento di estendere ai trilateri i teoremi già noti per i triangoli. In particolare Menelao sviluppa una teoria della congruenza per i trilateri per la quale valgono dei risultati che non hanno analoghi nel piano (come la congruenza di triangoli che hanno angoli a due a due congruenti). Nel Libro II, dopo due lemmi introduttivi relativi alla costruzione di un dato angolo in un dato punto di un arco di cerchio massimo, Menelao dimostra il teorema 3, fondamentale benché tecnico. Enuncia poi sei teoremi (4-9) riguardanti un trilatero diviso in strisce da cerchi paralleli a uno dei suoi lati, teoremi tutti dedicati al confronto delle misure di alcuni archi dati rispetto ad altri archi nella configurazione. Quindi, nei teoremi 10-13 del Libro II, non si riferisce mai ai trilateri bensì ai cerchi paralleli (cosa che non si riscontra in nessun altro luogo dell’opera). Considerato tutto ciò, sorge facilmente il sospetto che si tratti di un’opera molto vicina ai problemi del l’astronomia sferica.
Il Libro III si apre con l’enunciazione del teorema che sarà per Tolomeo e per gli altri astronomi antichi dopo di lui il principale teorema di trigonometria sferica, il cosiddetto ‘teorema di Menelao’ che, tra le altre cose, consente di trovare (in riferimento alla fig. 8) nei diversi gruppi di sei archi determinati dai punti A, B, G, D, E, F un dato arco conoscendo gli altri cinque archi del gruppo. Così, sempre in riferimento alla detta figura, il teorema afferma che (corda AE ):(corda ED)=(corda AB):(corda BF )=(corda FG):(corda GD). Questo teorema 1 non è formulato in termini di trilateri ma è espresso come un teorema relativo a quattro archi di cerchio massimo, ciascuno minore di un semicerchio. Il fatto che avrebbe potuto essere formulato in termini di trilateri fa pensare che Menelao lo abbia preso da un’opera più vecchia che non utilizzava i trilateri. Soltanto con il successivo teorema 2 si torna al linguaggio dei trilateri, con un risultato che è una forma più generale di un teorema noto agli scrittori arabi come la regola delle quattro quantità.
La dimostrazione del teorema 5 del Libro III presuppone che il lettore conosca già ciò che oggi chiameremmo l’invarianza del rapporto incrociato per archi di cerchio massimo, una cosa che mostra di nuovo come Menelao non stesse scrivendo degli ‘elementi’ di sferica per profani ma piuttosto per esperti (ne sono testimonianza i successivi teoremi 11-14, in cui Menelao presuppone la conoscenza di alcune relazioni trigonometriche). I teoremi 6-10 sono gli analoghi per i triangoli sferici dei teoremi di geometria avanzata per i triangoli piani, come quello secondo cui le altezze, o le mediane, si incontrano in un unico punto. Con i teoremi 11-14 si torna ad argomenti che hanno diretta attinenza con l’astronomia sferica, anche se sono formulati astrattamente. Il teorema 13 confronta, per vari archi nell’eclittica, i tempi di levata a sphaera recta (ascensioni rette) con i tempi di levata in regioni situate nelle zone polari; il teorema 14 confronta i tempi di levata per due regioni situate nelle zone polari e per due regioni situate al di fuori da queste zone. L’ultimo teorema dell’opera, il 15, offre l’equivalente di una formula che dovrebbe essere stata alla base delle tavole di ascensioni rette, come quella che si trova in Almagesto (II, 8), qualcosa che richiama alla mente Teodosio (Sphaerica, III, teoremi 11-12).
Nella versione del testo arabo di Menelao fatta da Gherardo da Cremona, questo teorema è accompagnato da una nota in cui si sostiene che il risultato si trova nel Liber aggregatus di Apollonio. La citazione di Apollonio è in sintonia con la promessa fatta da Menelao nell’introduzione di mettere in risalto le opere dei suoi predecessori, ove questi fossero nel giusto; d’altra parte, il passaggio non si trova nella redazione dell’opera che è stata fatta da Ibn 'Irāq, Abū Naṣr Manṣūr ibn 'Alī. Comunque sia, anche se la redazione di Abū Naṣr Manṣūr ibn 'Alī rispecchia più fedelmente il testo greco di quanto non faccia quella di Gherardo da Cremona, resta il fatto che qualche scrittore arabo ha creduto che questo teorema fosse dovuto ad Apollonio, e rimane una possibilità che ciò abbia, in effetti, qualche fondamento. In ogni caso, il teorema non è formulato in termini di trilateri e la sua conclusione ha un carattere molto diverso da quello dei teoremi precedenti, per cui esso appare un elemento appartenente ai primi tentativi di applicare la trigonometria alla sfera, dove «i diametri della sfera e dei circoli paralleli fornivano i primissimi strumenti per confrontare le lunghezze degli archi con le linee rette, e devono quindi essere considerati in un certo senso come le più antiche funzioni trigonometriche » (Björnbo 1902).
Infine, occorre ricordare che secondo Pappo (Collectio mathematica, IV, 55) Menelao scrisse un trattato sui tempi di tramonto degli archi nel semicerchio dell’eclittica che segue il Capricorno, affrontando un problema che era stato lasciato aperto da Euclide nei suoi Phaenomena.
La sferica nell’‘Almagesto’
Tolomeo dimostra nell’Almagesto di possedere una buona conoscenza del contenuto delle opere sulla sferica e ne pretende altrettanta nei suoi lettori. Relativamente al calcolo delle declinazioni degli estremi dei segni dell’eclittica (Syntaxis mathematica, I, 14), Tolomeo presuppone che il lettore sappia che l’arco di un cerchio massimo che passa per il polo di un secondo cerchio massimo ed è contenuto tra quel cerchio e il suo polo è un quarto di cerchio (una conseguenza di Teodosio: Sphaerica, I, teorema 16) e presuppone inoltre, con l’asserzione secondo cui un certo arco è uguale a un semicerchio, non soltanto la conoscenza di Teodosio, Sphaerica, I, teoremi 13 e 15, ma anche la capacità di utilizzarli per costruire un facile argomento.
L’assunzione in Almagesto, I, 12 secondo cui se due punti sono su un cerchio massimo che passa per i poli allora, quando la sfera ruota, essi si troveranno contemporaneamente sul meridiano, richiede poi un’applicazione sia di Teodosio (Sphaerica, II, teorema 10) sulla similitudine di due archi tagliati su cerchi paralleli da cerchi che passano per i poli, sia dell’inverso di Autolico (De sphaera quae movetur, teorema 3); ancora, quando Tolomeo assume (Almagesto, II, 3) che punti sull’eclittica equidistanti dai solstizi hanno la stessa declinazione (l’altezza sopra l’equatore), considera come acquisito un teorema di sferica, che, peraltro, non si ritrova in nessuno dei testi pervenutici. Infine si dà per scontato che il lettore conosca i teoremi fondamentali sulla congruenza dei trilateri, un termine che utilizza ma che (come ‘cerchio massimo’) non definisce.
I precedenti esempi potrebbero essere moltiplicati, ma sono già sufficienti a dimostrare che la conoscenza del corpo dei teoremi di sferica costituiva un requisito essenziale per comprendere l’Almagesto. Più che le asserzioni, sono importanti i teoremi di sferica dimostrati da Tolomeo. I primi esempi di questi teoremi sono nel Libro II dove egli mostra che punti sull’eclittica equidistanti dallo stesso equinozio determinano nel sollevarsi archi dell’orizzonte che sono uguali ma situati su lati opposti dell’equatore. Ciò deriva dal teorema 8 dei Phaenomena di Euclide e da questo Tolomeo deduce che la lunghezza del giorno, quando il Sole si trova in uno di questi due punti, è uguale a quella della notte quando il Sole si trova nell’altro punto. Egli non fornisce alcun argomento per giustificare questa conclusione, che è infatti una conseguenza immediata del teorema 19 degli Sphaerica di Teodosio (II). Altri teoremi compaiono in Almagesto (II, 7), nei quali, allo scopo di preparare il terreno per il calcolo dei tempi di levata a sphaera obliqua (ascensione obliqua), Tolomeo prova ciò che è dimostrato anche in Euclide (Phaenomena, teoremi 12 e 13), cioè che archi dell’eclittica che siano equidistanti dallo stesso equinozio si sollevano con archi uguali dell’equatore e che se due archi uguali dell’eclittica sono equidistanti dallo stesso solstizio la somma dei due archi dell’equatore che si sollevano con essi è uguale alla somme delle ascensioni rette degli stessi due archi.
Segue poi il teorema 10 sugli angoli tra l’eclittica e il meridiano, secondo cui gli angoli in punti dell’eclittica equidistanti dallo stesso equinozio (solstizio) sono uguali (sono insieme uguali a due angoli retti); in questo modo si generalizzano i risultati di Euclide (Phaenomena, teorema 2), relativi al caso in cui l’eclittica è perpendicolare al meridiano. Tolomeo dimostra poi, nel teorema 11, alcuni teoremi sugli angoli tra l’eclittica e l’orizzonte (per esempio il fatto che gli angoli tra l’eclittica e l’orizzonte in punti sull’eclittica equidistanti dallo stesso equinozio sono uguali) e, infine, nel teorema 12 dimostra quattro risultati simili a quelli che sono stati ricordati sopra sugli angoli formati dall’eclittica e dai paralleli di altezza.
Tutti questi teoremi differiscono dai teoremi di sferica precedenti l’epoca di Tolomeo, prima di tutto nelle dimostrazioni, poiché sono dimostrati utilizzando i risultati degli Sphaerica di Menelao e, in secondo luogo, nella loro apparente funzione, poiché non sono presentati come fine a sé stessi ma come preliminari al calcolo delle tavole dei tempi di levata e degli angoli. Può essere istruttivo riguardo al progresso che si è avuto nella sferica tra l’epoca di Euclide e quella di Tolomeo confrontare il trattamento euclideo degli angoli tra i cerchi massimi sulla sfera celeste con le tavole tolemaiche di angoli tra l’eclittica e il meridiano (Almagesto, II, 10).
Tolomeo scrisse altri due trattati anch’essi attinenti alla scienza della sfera: il primo è il Planispherium, che illustra per la prima volta il metodo che è alla base dell’astrolabio (anche se Tolomeo lo chiama appunto planispherium); l’altro trattato, costituito dagli Analemma, introduce un sistema di coordinate sulla sfera sul primo verticale e sul primo meridiano relativi a una certa regione. In quest’opera Tolomeo esemplifica l’uso di un metodo per rappresentare i cerchi sulla sfera in un piano di lavoro allo scopo di rappresentare archi e angoli sulla sfera in misura reale per risolvere problemi di astronomia sferica.
La scienza della sfera dopo Tolomeo: Pappo e Teone di Alessandria
Pappo, attivo durante l’ultima parte del III sec. e la prima parte del IV, ha lasciato una serie di note basate sulla sua lettura dei testi di Autolico, Euclide, Teodosio e Menelao discussi sopra, incorporate nel Libro VI della sua Collezione. Ciò fa pensare che a quell’epoca queste opere costituivano un gruppo di testi introduttivo per lo studio dell’astronomia. Uno scoliaste dell’opera di Pappo, infatti, ha aggiunto un’intestazione secondo cui «essa contiene le soluzioni di complicate questioni che si presentano nel dominio della piccola astronomia», riferendosi presumibilmente a una parte ristretta e più elementare di quella disciplina.
Sui commenti di Pappo è opportuno fare alcune osservazioni: (a) le nozioni che s’incontrano nei primi trattati di sferica conosciuti, ossia quelle di un arco di un cerchio «più grande di quello simile» a un arco di un altro e di due semicerchi di cerchi massimi ‘disgiunti’, continuano a costituire parte dell’apparato concettuale di Pappo; (b) la prima parte delle sue note, fino al teorema 26 del Libro VI, è dedicata alla dimostrazione dei teoremi 5 e 6 degli Sphaerica di Teodosio, Libro III, che continuava evidentemente a essere il manuale fondamentale (il successivo testo di Menelao poteva semmai servire a migliorarlo ma non a rimpiazzarlo); (c) in Collezione, VI, teorema 55, discutendo i Phaenomena di Euclide, Pappo si occupa delle questioni lasciate in sospeso dal teorema 12 dei Phaenomena, relative ai tempi di levata degli archi dell’eclittica nel semicerchio che segue il Cancro, ma si mantiene strettamente nei confini della vecchia sferica. Il risultato è che, nonostante nel teorema 57 del Libro VI sia in grado di risolvere il problema per la sphaera recta, nei successivi teoremi 58-60 egli può soltanto discutere dei casi speciali in sphaera obliqua, ed è qui che si menzionano le opere di Ipparco e di Menelao. Infine, egli riconosce che i tempi sono cambiati dall’epoca in cui furono scritti questi trattati e chiude il libro avvertendo lo studente che il proprio approccio gli potrà fornire soltanto una conoscenza imperfetta di queste cose e che farebbe meglio, pertanto, a consultare le opere di Tolomeo sull’argomento. Un’altra informazione di rilievo si trova poi nel Libro V della Collezione, quando Pappo si riferisce a un gruppo di «lemmi di Sferica» per la dimostrazione del risultato secondo cui se un angolo α è maggiore di un angolo β, allora tanα/tanβ è maggiore di α/β. Circa mezzo secolo dopo che Pappo di Alessandria aveva scritto i suoi commentari, Teone, anch’egli di Alessandria, scrisse i suoi e, fortunatamente, il commentario di Teone sull’Almagesto di Tolomeo pervenutoci comprende la parte relativa ai primi due libri, poiché i teoremi di sferica attengono principalmente a queste parti dell’opera. Nei commentari di Teone ai libri I e II dell’Almagesto s’incontrano frequenti i riferimenti – alcuni espliciti, altri taciti – a scritti di sferica. Sono soprattutto tenuti presenti i tre libri degli Sphaerica di Teodosio, ma sono anche considerati il De habitationibus di Teodosio, il De sphaera quae movetur di Autolico e gli Sphaerica di Menelao. Anche Teone, come Pappo, utilizza le nozioni di ‘semicerchi asintotici’ e di un arco di un cerchio «più piccolo di quello simile» a un arco di un altro cerchio, e, come Tolomeo, egli non fa alcuna menzione di Menelao in relazione alla discussione del teorema di quest’ultimo.
A testimoniare che il coinvolgimento di Teone con la sferica sia andato al di là del leggere i testi e dell’applicare quanto ha scritto per spiegare alcuni punti dell’Almagesto, c’è una nota dell’anonimo autore dell’opera Sulle figure isoperimetriche, nella quale si rimanda – per una dimostrazione del risultato relativo agli archi α, β, menzionato nella precedente discussione di Pappo – a «Teone nel commentario sulla piccola astronomia». Il riferimento sembra essere a un commentario di Teone su quello stesso dominio di conoscenza che lo scoliaste riferiva a Pappo, cioè quello noto come la ‘piccola astronomia’, che comprende i trattati di sferica di Euclide, Autolico e Teodosio. In ogni caso, Teone scrisse effettivamente un trattato sull’astrolabio, di notevole influenza sugli scrittori islamici medioevali, utilizzando probabilmente per primo tale termine (evidentemente con l’epiteto ‘piccolo’) per denotare uno strumento piano. L’astrolabio forniva un utile strumento portatile che, tra le altre cose, serviva per istruire sui problemi della astronomia sferica e per calcolare le ore trascorse del giorno o della notte.
Con Teone si conclude questa rapida esposizione della storia della sferica greca. È vero che Proclo, basandosi fortemente su Gemino, scrisse un’opera intitolata Sphaera, ma questa va considerata più come uno sviluppo di una tradizione letteraria che come un’opera del livello di quella Pappo o di quella di Teone, per citare solamente questi due autori. Nuovi e significativi sviluppi della materia, principalmente nel campo della trigonometria sferica, si avranno soltanto con gli scrittori dell’Islam medievale.
Qualunque cosa si possa pensare circa la verosimiglianza dell’esistenza di un corpus dottrinale greco chiamato La piccola astronomia, si sa che, almeno fin dal IX sec. d.C., gli autori arabi hanno riunito le opere che abbiamo discusso, insieme a poche altre, in una collezione detta I libri intermedi. Si trattava di opere che dovevano essere studiate dopo aver appreso gli Elementi di Euclide ma prima di affrontare l’Almagesto, ed è probabile che questo corpus includesse tutti quei testi che lo studente avrebbe incontrato con ogni probabilità nei commentari sull’Almagesto. Perciò esso comprendeva tutte le opere menzionate da Pappo nel Libro VI della Collectio, quali il trattato Sulle grandezze e le distanze del Sole e della Luna di Aristarco di Samo e l’Ottica di Euclide, nonché le altre opere menzionate da Teone nel suo commentario sull’Almagesto, quali i Dati di Euclide, il Sulla sfera e sul cilindro e la Misura del cerchio di Archimede. Di tutte queste opere fu fatta una scrupolosa edizione nel XIII sec. da parte di al-Tūsī, Naṣīr al-Dīn e il loro studio rimase parte del curriculum fondamentale dell’istruzione scientifica. Non a caso, nel momento in cui questo stesso scrittore si accinse a fornire il primo trattamento della trigonometria piana e di quella sferica indipendente dall’astronomia, egli scelse come parola chiave del titolo il concetto chiave del libro, cioè la ‘figura trasversale’, riferendosi perciò a quello stesso teorema che apre il Libro III degli Sphaerica di Menelao e che offrì a Tolomeo il principale risultato per il suo trattamento dei teoremi relativi alla sfera. In questo senso, la storia della sferica illustra una regola generale della storia della matematica, vale a dire la natura conservatrice della tradizione matematica e la dipendenza di parti successive di quella scienza da tradizioni vecchie di secoli.
Bibliografia
Aujac 1984: Aujac, Germaine, La langue formulaire dans la géométrie grecque, “Revue d’histoire des sciences et leurs applications”, 37, 1984, 2, pp. 97-109.
Berggren 1991: Berggren, John L., The relation of Greek spherics to early Greek astronomy, in: Science and philosophy in classical Greece, edited by Alan C. Bowen, New York, Garland, 1991, pp. 227-248.
Björnbo 1902: Björnbo, Axel, Studien über Menelaos Sphärik. Beiträge zur Geschichte der Sphärik und Trigonometrie der Griechen, “Abhandlungen zur Geschichte der Mathematischen Wissenschaften mit Einschluss ihrer Anwendungen”, 14, 1902, pp. 1-134.
Heath 1921: Heath, Thomas L., A history of Greek mathematics, Oxford, Clarendon Press, 1921, 2 v. Mueller 1980: Mueller, Ian, Ascending to problems: astronomy and harmonics in Republic VII, in: Science and the sciences in Plato, edited by John P. Anton, New York, EIDOS; Delmar (N.Y.), Caravan Books, 1980, pp. 103-121.
Neugebauer 1975: Neugebauer, Otto, A history of ancient mathematical astronomy, Berlin-New York, Springer-Verlag, 1975, 3 v.
Schmidt 1943: Schmidt, Olaf Henrik, On the relation between ancient mathematics and spherical astronomy, Providence (R.I.), Brown University, 1943.
– 1952: Schmidt, Olaf Henrik, Some critical remarks about Autolycus’ On risings and settings, in: Den 11te skandinaviske matematikerkongress i Trondheim 22-25 august 1949, redigert av R. Tambs Lyche, Oslo, I kommisjon hos J.G. Tanum, 1952, pp. 202-209.