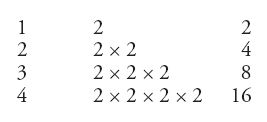Scienza greco-romana. La scienza greca e l'Oriente
Scienza greco-romana. La scienza greca e l'Oriente
La scienza greca e l'Oriente
La scienza e la filosofia sono state a lungo considerate il frutto del 'miracolo greco', un frutto incomparabile con quello prodotto dalle civiltà anteriori, nella fattispecie quella mesopotamica e quella egizia. Oggi questa concezione, se non abbandonata, è perlomeno considerata troppo radicale; comunque si giudichino i suoi meriti, la Grecia ha certamente subìto l'influenza di queste civiltà e ne ha elaborato i prestiti in modo originale.
L'Egitto, la Mesopotamia, il Vicino Oriente e quel che diventerà poi la Grecia furono in rapporto fin dall'Alta Antichità; già nel Neolitico, il Mar Egeo era una via di comunicazione tra l'Asia Minore, le isole e la Grecia continentale, e intorno al 3000 furono importate in Grecia le tecniche metallurgiche del Vicino Oriente. In alcune tombe tebane dell'epoca di Thutmosi III (1500 ca.) appaiono rappresentazioni di portatori di offerte detti Keftiu, generalmente considerati cretesi, e i documenti egizi di Tell el-Amarna attestano l'esistenza di relazioni con le popolazioni del Vicino Oriente e della Mesopotamia. Nel XIV e XIII sec. gli archivi hittiti fanno menzione di un regno degli achchiyawa, probabilmente gli Achei (i Greci). In Siria e in Egitto sono stati ritrovati oggetti cretesi e micenei, in particolare ceramiche.
Questi rapporti sono accertati anche per epoche più recenti, sia che fossero diretti sia che passassero per il tramite dei navigatori e dei commercianti fenici. Cipro e Ugarìt sembrano essere stati importanti luoghi di scambio, a causa della loro posizione geografica e degli eventi storici; così, Cipro, dapprima appartenente alla sfera cretese-micenea, nel X sec. annoverava insediamenti commerciali fenici e in seguito fu conquistata dagli Assiri (alla fine dell'VIII sec.), dagli Egizi e infine dai Persiani.
Tra il VI e il V sec. gli scambi s'intensificarono grazie all'avanzata verso ovest degli imperi mesopotamici, alle successive conquiste dell'Egitto e poi alle guerre persiane. In un primo tempo l'Egitto fu conquistato dagli Assiri (Tebe fu sottomessa da Assurbanipal nel 663); ritrovò poi brevemente la propria indipendenza grazie alla disgregazione dell'Impero assiro, ma nel 525 cadde in mano ai Persiani e vi restò fino al 405.
Ancor prima che Cambise conquistasse l'Egitto, Ciro, il fondatore dell'Impero persiano nel 539, aveva esteso le sue conquiste in direzione dell'Asia Minore e della Lidia di Creso. Le città greche della costa ionica caddero allora in mano ai Persiani, che le affidarono ad alcuni tiranni alle loro dipendenze. Nel 499, con la rivolta delle città ioniche sostenute da Atene, ebbero inizio le guerre persiane. Mileto fu distrutta nel 494; Dario voleva estendere la dominazione persiana alla Grecia continentale, ma nel 490 fu sconfitto a Maratona. Serse riprese l'offensiva, ma nel 479 fu sconfitto a sua volta e le città ioniche furono liberate. In questo periodo di tutela e poi di guerra le idee elaborate nei diversi imperi mesopotamici ebbero modo di penetrare nella civiltà greca, allora in piena trasformazione; questa civiltà (rappresentata, per es., a Mileto da Talete, Anassimandro e Anassimene, a Efeso da Eraclito e a Samo da Pitagora) cominciò a spostarsi dalla costa ionica verso la Grecia continentale. In linea generale, si ebbe una commistione di popoli e uno spostamento verso ovest di tutta la civiltà (Roma, miticamente fondata nel 753 a.C., emerse veramente soltanto alla fine del VII sec.) e nel VI sec. la Grecia divenne un centro di intensi scambi marittimi tra gli imperi orientali e l'Occidente che cominciava a civilizzarsi (Italia, Gallia, Iberia).
Più tardi, nella seconda metà del IV sec., le conquiste di Alessandro Magno (356-323) intensificarono i rapporti tra il mondo greco, l'Oriente e l'Egitto; ne derivò una ellenizzazione di queste regioni, ma anche l'aumento delle influenze orientali ed egizie sulla Grecia. In questa fase, però, la civiltà greca era già radicata e le sue basi erano poste, per cui le influenze su di essa furono meno forti.
La filosofia e la scienza greca nacquero quindi in un periodo agitato e particolarmente aperto ai contatti, sia pure di natura bellica, tra la Grecia, l'Egitto e l'Oriente, sia quello vicino sia quello più lontano; nonostante rapporti così stretti, però, le civiltà non si fusero e neppure si verificò una commistione di idee di particolare importanza, perlomeno non prima del periodo ellenistico.
Testimonianze greche
Gli stessi Greci si dicevano debitori di alcune conoscenze alle civiltà orientali e a quella egizia. Erodoto nelle Storie (II, 109) attribuisce agli Egizi l'invenzione della geometria, che sarebbe stata loro necessaria per tracciare i limiti dei campi, cancellati annualmente dalle piene del Nilo. Sempre Erodoto attribuisce ai Babilonesi l'invenzione dello gnomone, del quadrante solare e della divisione del giorno in dodici parti uguali dal levare al tramontare del Sole. Secondo Porfirio di Tiro nella Vita di Pitagora (6), il matematico greco avrebbe appreso la geometria dagli Egizi, l'aritmetica dai Fenici e l'astronomia dai Caldei. Ippolito di Roma, nei Philosophoumena (I, II, 12) fa viaggiare lo stesso Pitagora in Oriente, dove gli fa incontrare Zoroastro; Isocrate, nel Busiride (28), afferma che avrebbe acquisito le sue conoscenze in Egitto. Secondo Proclo di Costantinopoli, Talete avrebbe appreso la geometria in Egitto (In primum Euclidis elementorum librum commentarii), e Diogene Laerzio precisa che in Egitto Talete calcolò l'altezza delle piramidi a partire dalla loro ombra (Vitae philosophorum, I, 27). Ippocrate di Coo (460 ca.-377/360) avrebbe appreso la medicina a Menfi, in Egitto; sarebbe stato poi Cadmo, figlio di un re fenicio e fratello di Europa, ad aver inventato e introdotto la scrittura in Grecia (l'alfabeto greco deriva in effetti dalla scrittura consonantica fenicia). Si hanno quindi, da parte degli stessi Greci, numerosissime allusioni a prestiti venuti dall'Egitto, da Babilonia e dal Vicino Oriente, il riconoscimento dei quali non impediva però un certo spirito critico; così, per Platone (Respublica, IV, 435 e) i Greci erano caratterizzati dal loro amore per il sapere, mentre i Fenici e gli Egizi brillavano soprattutto per il loro amore per la ricchezza, e ciò attesta la coscienza della differenza tra un sapere greco (un sapere 'puro') e un sapere egizio (maggiormente rivolto alle applicazioni). Non bisogna però trarne conclusioni affrettate, e privare troppo rapidamente Egizi, Fenici e Babilonesi di un sapere disinteressato, fosse anche il frutto di una semplice curiosità, soltanto perché non è sotteso di una filosofia comparabile a quella di Platone.
I documenti
Oltre ai dati storici e alle testimonianze greche, esistono numerosi documenti relativi alle 'scienze' elaborate da queste civiltà orientali; tuttavia, da un lato questi documenti sono molto frammentari ‒ e quindi non possono fornirci più di qualche ragguaglio sulle scienze dell'epoca ‒ e dall'altro lato sono di natura diversa a seconda delle civiltà.
V'è prima di tutto una differenza nel tipo di scrittura. I documenti mesopotamici sono scritti con caratteri cuneiformi, i documenti egizi in geroglifici (in ieratico o in demotico, secondo le epoche e la natura dei documenti), mentre i Greci si servono di un alfabeto.
La scrittura mesopotamica e quella egizia, pur avendo subìto un'evoluzione che ne ha accresciuto l'aspetto fonetico, sono sempre rimaste in larga misura ideografiche e lontane dal fonetismo totale caratteristico della scrittura alfabetica greca; la scrittura fenicia, da cui deriva l'alfabeto greco, era fonetica ma indicava soltanto le consonanti, come spesso avveniva nelle lingue semitiche.
La scrittura ideografica mal si prestava all'annotazione delle articolazioni grammaticali, e quindi delle nozioni complesse; era più facile documentare conoscenze 'positive', fattuali, che non lo spirito in cui queste conoscenze erano concepite. Questo spirito poteva essere trasmesso più facilmente, invece, da una scrittura alfabetica, più adatta a rendere conto delle sottigliezze del pensiero. Siamo dunque meno informati sulla forma mentis dei Mesopotamici e degli Egizi che su quella dei Greci.
Oltre alla differenza di scrittura, c'è una differenza nella natura dei documenti stessi. L'imputrescibilità dei materiali o la mitezza del clima hanno conservato fino ai nostri giorni i documenti mesopotamici (tavolette d'argilla) e quelli egizi (papiri); i documenti greci d'epoca, invece, sono molto rari. Disponiamo soltanto della tradizione riportata da autori, di norma leggermente posteriori, i cui scritti ci sono stati trasmessi attraverso copie successive, sia nella lingua d'origine, sia in traduzione, con tutti i conseguenti rischi d'alterazione: questa modalità di trasmissione ha comportato anche una selezione dei testi. Così, se, insieme a testi che erano senza dubbio di tipo erudito, ci sono giunti documenti mesopotamici ed egizi che sembra fossero semplici 'quaderni di scuola', per la Grecia non disponiamo di alcun 'esercizio scolastico' di questo genere (visto che a nessuno sarebbe venuto in mente di copiarlo nel corso dei secoli), ma ci rimane traccia unicamente dei lavori che erano considerati importanti. Con ogni probabilità, proprio come la diversità della scrittura, anche questo ha indotto una deformazione nel nostro modo di considerare la scienza che questi testi documentano.
Influenze mesopotamiche ed egizie
Per individuare all'interno della scienza greca gli elementi di continuità con quella mesopotamica e quella egizia (prima del periodo ellenistico in cui, con le conquiste di Alessandro Magno, le civiltà si sono un po' amalgamate), in primo luogo va ricordato che in Oriente, molto prima che in Grecia, esistevano discipline distinte. Una di esse aveva come oggetto i numeri e il calcolo (quel che si chiamerà 'aritmetica'), un'altra lunghezze, superfici e volumi (la 'geometria'), una terza gli avvenimenti celesti (astri e fenomeni meteorologici, più o meno confusi in una specie di 'astronomia') e un'ultima le malattie (la 'medicina', che poteva comprendere o no una fisiologia dello stato di salute). Questa ripartizione in discipline esiste anche in altre culture prive di ogni rapporto con quelle di cui ci occupiamo (per es., quella cinese), ma in un caso come questo è legittimo pensare che la civiltà meno sviluppata (quella greca) abbia potuto attingere a quelle più sviluppate; in altre parole, si sarebbe trattato di un'importazione, invece che di un'invenzione autonoma.
Allo stesso modo, la Grecia ha probabilmente importato, adattandoli, i rudimenti delle varie discipline scientifiche (così come ha importato la propria scrittura dalla Fenicia modificandola per adattarla alla propria lingua e indicando le vocali): per esempio, la numerazione a base decimale, che a Creta e in Grecia era uguale a quella egiziana; le operazioni di calcolo, semplici (addizione, sottrazione, moltiplicazione, divisione) o più complesse (potenze e radici); il calcolo di aree e volumi elementari; certamente alcune nozioni basilari di astronomia (Zodiaco, eclittica, pianeti). Tutte queste cose la Grecia avrebbe potuto certamente scoprirle in modo autonomo, ma, visto che esistevano già presso civiltà con le quali essa era in comunicazione, potrebbero anche essere state mutuate da queste e adattate. Probabilmente il carattere elementare e 'culturalmente neutro' di queste conoscenze ne rendeva possibile l'acquisizione, mentre gli aspetti più complessi della scienza mesopotamica ed egizia erano difficilmente assimilabili da una Grecia ancora ai primordi.
Analoghe considerazioni possono essere fatte in relazione a nozioni un po' più raffinate; per esempio, nella misura in cui in Mesopotamia e in Egitto si trova 'qualcosa' che somiglia all'uso di quelli che chiamiamo i teoremi di Talete e di Pitagora, è legittimo supporre che questo 'qualcosa' sia stato importato in Grecia (forse da Talete e Pitagora) e sia stato poi riformulato dallo spirito greco sotto forma di teoremi (di certo molto dopo Talete e Pitagora). D'altra parte, la tradizione riferita da Diogene Laerzio, secondo cui, com'è stato ricordato in precedenza, Talete avrebbe calcolato l'altezza delle piramidi misurando la lunghezza della loro ombra e comparandola con quella di un bastone piantato nel terreno (fatto che implica l'uso del teorema sui triangoli simili), vuole certamente evocare l'origine egizia di questa conoscenza.
Si possono fare osservazioni simili anche per l'astronomia. La dossografia attribuisce a Talete la previsione di un'eclissi solare durante "la guerra tra i Medi e i Lidi" (Clemente Alessandrino, Stromata, I, 65, il quale cita la Storia astronomica di Eudemo). Ammettendo che Talete abbia realmente predetto questa eclissi, egli ha potuto farlo soltanto derivando le sue conoscenze da qualche astrologo mesopotamico, forse senza neppure capire i principî astronomici impiegati. Ciò non esclude che alcuni di questi principî possano essere stati usati, molto più tardi, in Grecia.
Nel caso della medicina vi sono alcune convergenze più o meno marcate, per esempio per quanto riguarda il ruolo del cuore. Secondo il papiro Ebers (1550 ca.), il corpo è attraversato da una rete di 'tubi' nei quali circola ogni genere di fluidi, e certamente anche i 'soffi' (il "soffio di vita" e il "soffio di morte", menzionati nel testo); il cuore vi predomina e comanda gli altri organi, ai quali 'parla' tramite i vasi. Anche la fisiologia di Aristotele attribuisce una funzione centrale al cuore, sede dell'anima e quindi della vita; nei trattati ippocratici e aristotelici si sostiene persino che a partire dal cuore, dove si riscalda, l'aria proveniente dai polmoni si diffonde in tutto il corpo attraverso le arterie. In tal modo questo "soffio caldo" ‒ il 'pneuma' ‒ vivifica il corpo. In questo caso è evidente l'analogia con la tesi egizia secondo cui esiste un "soffio di vita" e il cuore 'parla' alle varie parti del corpo attraverso i vasi.
Anche alcune nozioni 'parascientifiche' potrebbero essere state importate, a meno che non derivino da un fondo comune molto antico. Così, la cosmologia di Talete, fondata sull'acqua, ricorda il mito greco di Oceano descritto da Omero nell'Iliade (XIV, 201, 246, 302) e da Aristotele nella Metafisica (I, 3, 983 b 30), ma corrisponde anche alla concezione sumera secondo cui la Terra è incastonata tra le acque inferiori e quelle superiori, e alla cosmologia che si può leggere tra le righe della Bibbia (soprattutto nella Genesi, 1, 6-9). Un altro esempio dello stesso genere si ritrova nei pitagorici, per i quali i numeri dispari erano maschili e quelli pari femminili. Quest'idea prefigura la teoria dell''uno' e della 'diade' che Aristotele, nella sua Metafisica (XIV, 1, 1087 b), attribuisce ai platonici (verosimilmente Speusippo e Senocrate), ma che numerosi dossografi dicono pitagorica; teoria secondo la quale l''uno' è l'unità determinativa (dispari e maschile), mentre la 'diade' è la potenza moltiplicativa (pari e femminile), e la loro congiunzione genera i numeri. Ora, nella numerazione sumera, il numero 1 si dice gesh, che significa anche 'uomo, maschio', mentre il numero 2 si dice min, che significa anche 'donna, femmina' (Guitel 1975). Tra queste concezioni vi è un legame evidente, anch'esso però probabilmente derivato da un antico fondo comune più che da un prestito; un fondo che traspare anche nel calcolo egizio, in cui le moltiplicazioni erano effettuate attraverso una serie di duplicazioni successive (con addizione dell'opportuno prodotto parziale), un po' come se la duplicazione (il due, la diade) fosse il mezzo per eccellenza per generare la molteplicità.
La lista delle conoscenze comuni o mutuate potrebbe continuare, ma sarebbe cosa lunga e noiosa; è praticamente impossibile affermare con certezza che tale conoscenza sia stata mutuata e talaltra no, ed è certamente più utile cercare di indicare i limiti di questi prestiti, limiti inerenti ad alcune differenze nello spirito stesso della scienza. Lo faremo, per mezzo di esempi, nel caso della matematica, dell'astronomia e della medicina.
Matematica babilonese e matematica pitagorica
Sia i matematici babilonesi che i pitagorici aderivano a una mistica numerica. Simili mistiche sono assai diffuse in tutto il mondo e sono di vario tipo. Quelle di cui ci occupiamo qui si fondano evidentemente sulla difficoltà di precisare la natura dei numeri. Qual è il livello di definizione dei numeri? Essi non appartengono al mondo della Natura eppure sembrano governarlo, poiché si applicano ad esso sotto forma di leggi aritmetiche (in particolare, nell'astronomia babilonese o nella musica pitagorica). Le figure geometriche, per quanto siano astratte, conservano un aspetto sensibile che conferisce alla geometria elementare l'apparenza di una scienza naturale. I numeri sono privi di questa dimensione sensibile e quasi concreta, e di conseguenza scivolano facilmente verso la mistica e il soprannaturale. A Babilonia i numeri erano associati agli dèi, a cui era accordato un valore numerico più o meno grande a seconda della loro posizione nella gerarchia del pantheon. Anu, dio del cielo, divinità principale, era associato al numero 60, base della numerazione; Enlil, suo figlio, dio della Terra, al numero 50; Sin, il dio della Luna, al 30; e così via; i piccoli demoni di scarsa importanza dovevano accontentarsi di frazioni (Bottéro 1952).
Al posto di questa gerarchia puramente quantitativa, i pitagorici facevano uso di un ordine più sofisticato: invece del semplice valore quantitativo crescente (caratteristico della progressione, una delle nozioni preferite dai Babilonesi, in particolare nell'astronomia), ricorrevano a un 'valore strutturale' che riguardava o il numero in sé o i suoi rapporti con gli altri numeri. Tuttavia questo valore strutturale non era sempre ben definito, né il suo interesse matematico sempre accertato. Così, i pitagorici accordavano una grande importanza al numero 10, base della numerazione greca; mentre però i Babilonesi attribuivano la supremazia al 60 ‒ che associavano alla loro principale divinità ‒ semplicemente perché era la base della loro numerazione, i pitagorici giustificavano l'importanza del numero 10 con argomenti che riguardavano la sua 'struttura'. Tali argomenti sono specificati in un frammento attribuito a Speusippo, nipote e successore di Platone a capo dell'Accademia, e si basano, tra l'altro, sul fatto che 10 contiene un uguale numero di pari e di dispari, di numeri primi e composti, essendo la somma di 1, 2, 3 e 4 (fig. 3), i quali rappresentano rispettivamente il punto, la linea, il piano e il volume.
Queste spiegazioni, che appaiono un po' stravaganti, rivelano come si attribuisse al numero un valore non derivato semplicemente dalla sua posizione all'interno di una gerarchia quantitativa. I pitagorici non giustificavano la preminenza del 10 associandolo alla divinità suprema di un pantheon; cercavano piuttosto quanto potesse spiegare, nel modo stesso in cui questo numero era stato formato e strutturato, la sua particolare importanza nella numerazione (di cui era la base), e quindi nell'aritmetica, se non addirittura nella geometria.
Anche altri numeri avevano un valore particolare. I numeri 'perfetti', 'abbondanti' o 'deficienti' erano, rispettivamente, quelli uguali, inferiori o superiori alla somma dei loro divisori; due numeri erano considerati 'amici' quando ognuno era uguale alla somma dei divisori dell'altro, e i numeri 'primi' avevano come unici divisori il numero stesso e 1.
La caratterizzazione dei numeri rimandava quindi alla loro struttura o al modo in cui erano formati; essi, inoltre, erano in diverso rapporto tra loro a seconda che rispettassero le proporzioni aritmetiche, geometriche, armoniche, musicali e così via. Queste proporzioni, che avevano un'importanza particolare nella matematica pitagorica, tessevano così ogni sorta di rapporti tra i numeri. Il mondo pitagorico dei numeri, dunque, era molto più complicato di quello mesopotamico e considerava i numeri all'interno di una varietà di rapporti molto più sofisticati di una semplice gerarchia quantitativa associata a un pantheon.
Questa stessa diversità di concezione s'incontra nell'uso dei numeri nella matematica. Alcuni problemi mesopotamici sembrano essere stati concepiti a partire da tabelle di calcolo; in linea generale, infatti, la semplice osservazione di queste tabelle permette di scorgere ogni sorta di rapporti tra i numeri, dei quali ci si può servire per la risoluzione di problemi. Sia data, per esempio, una tabella delle potenze successive di 2, di cui abbiamo qualche esempio (come la tavoletta MLC 2078, I dinastia babilonese):
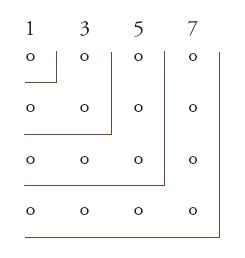
In questa tabella si nota l'esistenza di rapporti tra 2, 3 e 8, che indichiamo come 2³=8 o come log₂8=3. Anche se la nozione di potenza (che è una nozione semplice) e, a fortiori, quella di logaritmo (che è più complessa) non sono astratte e non sono colte in tutta la loro generalità, nella tabella i corrispondenti rapporti tra numeri sono abbastanza facilmente percepibili e potranno essere usati nelle strategie di calcolo e per la risoluzione di vari problemi. Anche i pitagorici hanno osservato i numeri e i loro rapporti, ma in altro modo e precisamente in quello della raffigurazione geometrica, in cui ogni unità era rappresentata da un punto e i punti erano disposti in figure geometriche diverse (quadrati, rettangoli, triangoli, cubi e così via). Questa raffigurazione, che forse derivava da una certa scomodità della numerazione greca scritta, evidenziava varie proprietà aritmetiche; così, per esempio, si poteva rappresentare la serie dei numeri dispari nel modo seguente, in cui ognuno di essi era raffigurato da uno gnomone (una squadra):
Ciò permetteva di visualizzare ‒ e di concepire ‒ la proprietà aritmetica per cui la somma di numeri dispari successivi era un quadrato (1+3=4=2², 1+3+5=9=3², e così via). Questa proprietà caratterizzava i numeri in sé stessi e, anche se poteva rientrare in una strategia di calcolo, non si limitava alla sola funzione pratica (contrariamente all'esempio precedente, in cui i numeri non erano colti nella loro struttura, ma soltanto in quanto inclusi in una tabella da cui emergevano unicamente le proprietà utilizzabili per il calcolo).
Vi era dunque una netta differenza nel modo di concepire i numeri; a Babilonia erano considerati nell'ambito del calcolo, ossia di un'efficacia pratica, e a questo si aggiungeva l'associazione alle divinità secondo la gerarchia del pantheon, che rendeva conto del carattere 'soprannaturale' dei numeri e forse poteva giustificare l'efficacia degli usi pratici dell'aritmetica, mentre invece i Greci consideravano i numeri di per sé, come un mondo autonomo con caratteri propri, indipendentemente dalle applicazioni pratiche e da qualsiasi associazione agli dèi. La raffigurazione geometrica ne facilitava l'intelligibilità (dopo la scoperta degli irrazionali, i 'numeri-punto' cederanno il posto ai 'numeri-segmento'). Tuttavia, al di là di questa raffigurazione, il loro livello di esistenza restava di difficile individuazione, e da questo derivava la mistica numerica pitagorica (che però era una mistica più aperta, e, soprattutto, più svincolata dal calcolo e dalle applicazioni pratiche).
Si possono fare osservazioni simili anche nel caso della geometria, nel cui ambito, in Grecia, la preoccupazione per le figure in sé stesse si traduceva nella ricerca di dimostrazioni, laddove l'Egitto e la Mesopotamia s'interessavano alle applicazioni pratiche, tollerando le approssimazioni. Tuttavia, la questione dello statuto degli oggetti della geometria era meno viva di quella dello statuto dei numeri; apparentemente la Mesopotamia e l'Egitto la ignorarono e la Grecia se ne preoccupò solamente più tardi, quando la sua filosofia, dopo la scoperta dei numeri irrazionali, passò da una mistica numerica a un 'dio geometra'.
Astronomia babilonese e astronomia greca
A Babilonia gli astri, come i numeri, erano legati al sacro; anche se non erano assimilati agli dèi, si riteneva tuttavia che li accogliessero o li rappresentassero. L'astronomia era soprattutto un'astrologia, ma dotata di una struttura matematica, come attestano alcune tavolette del periodo seleucidico (Neugebauer 1955). Allora la Mesopotamia era sotto la dominazione di una dinastia greca, ma i metodi esposti dalle tavolette non avevano nulla di greco (anche se furono utilizzati dall'astrologia ellenistica; Neugebauer 1951) e verosimilmente risultavano da una tradizione locale più antica, della quale erano il coronamento. Quest'astronomia matematica faceva uso di calcoli fondati su progressioni aritmetiche, senza ricorrere a modelli geometrici del moto degli astri.
Le progressioni erano presenti nella matematica babilonese indipendentemente dall'astronomia, e molto prima dell'epoca seleucidica (per es., nella tavoletta STR 362, I dinastia babilonese). Le troviamo anche in Egitto (Problemi 40, 64 e 79 del papiro Rhind), ma gli Egizi non ne facevano uso nell'astronomia, mentre i Babilonesi se ne servivano per calcolare la posizione degli astri 'mobili' (Sole, Luna e pianeti), generalmente in occasione di fenomeni particolari (apparizione o scomparsa di un astro, fasi della Luna, e così via). Queste posizioni, osservate o calcolate, erano espresse per mezzo di quelle che oggi chiameremmo 'coordinate angolari' in rapporto all'eclittica e allo Zodiaco. L'osservazione forniva le coordinate di un certo astro in una certa data e, per conoscere la sua posizione in un'altra data, bisognava applicare a queste coordinate un sistema di progressioni aritmetiche.
Se nell'astronomia i Babilonesi usavano l'aritmetica piuttosto che la geometria, è probabilmente per due ragioni. In primo luogo, forse il calcolo della posizione di un astro era effettuato prendendo a modello la formazione dei numeri; la posizione di un astro (rappresentata da coordinate, che erano numeri) comportava infatti la sua posizione ulteriore secondo una progressione o una combinazione di progressioni, così come un numero ne generava un altro secondo una progressione. In secondo luogo, tra numeri e tempo esisteva un rapporto quasi naturale. Nella numerazione i numeri si susseguivano in successione temporale, secondo un ordine quantitativo crescente; era una progressione aritmetica (con ragione 1) svolta nel tempo, una produzione temporale dei numeri. In questo caso il tempo non era comparabile a una dimensione come quella spaziale, non era un tempo geometrizzato, bensì il tempo della parola che enumerava, un tempo scandito, un ritmo. Di conseguenza l'aritmetica ‒ in special modo le progressioni ‒ s'imponeva quando era necessario determinare un elemento futuro, e ciò soprattutto se si trattava di astronomia, visto che gli astri da sempre servivano a misurare e a scandire il tempo (il ricorrere dei giorni, dei mesi e degli anni), e che a Babilonia erano associati agli dèi, i quali, a loro volta, erano collegati alla mistica dei numeri, e così la scansione del tempo per mezzo degli astri e la scansione per mezzo dei numeri convergevano.
Il calcolo astronomico, quindi, si serviva di una specie di algoritmo, stabilito verosimilmente a partire da tabelle di osservazioni che registravano la posizione degli astri per periodi molto lunghi. Per noi, il modello geometrico del moto degli astri rende intelligibile e trasparente il calcolo della loro posizione; a Babilonia, invece, l'inesistenza di quest'aspetto geometrico faceva sì che l''algoritmo astronomico' fosse quasi una formula divinatoria, una formula aritmetica che dava un risultato la cui esattezza era verificata con l'osservazione (ma una formula la cui veridicità si fondava unicamente su quest'osservazione).
Ciò aveva due conseguenze: da un lato, nel calcolo ci si accontentava di un'approssimazione, poiché si cercava di prevedere la posizione di un astro piuttosto che renderne intelligibile il moto, e, dall'altro lato, in mancanza del modello geometrico che l'avrebbe resa intelligibile, la coincidenza approssimativa tra il risultato calcolato e la realtà osservata era certamente rapportata alla mistica, in cui numeri, astri e divinità erano legati da misteriosi rapporti. L'astronomo era un mago, che si serviva di formule da scoprire esplorando il mondo divino degli astri (cosa resa possibile da vari strumenti di osservazione) e il mondo mistico dei numeri.
In Grecia, al contrario, fece la sua apparizione un'astronomia essenzialmente geometrica, con una conseguenza importante, chiaramente evidenziata in Platone e in Eudosso ma che già traspare nei pitagorici. L'astronomia greca, infatti, cercava di ricondurre il moto apparente degli astri (particolarmente erratico nel caso dei pianeti) a un moto circolare uniforme o a una combinazione di moti circolari uniformi. Questa regolarità circolare privava il moto di ogni possibilità di modificazione, ne faceva una semplice ripetizione dell'identico, riconduceva regolarmente l'astro alla stessa posizione e l'orbita diventava l'insieme di queste posizioni periodiche più che la traiettoria di un mobile.
Ciò significava negare, se non il moto, almeno il cambiamento che tale moto avrebbe provocato ed equivaleva, per converso, a una sorta di affermazione della permanenza e dell'eternità degli astri (il moto circolare era il moto eterno per eccellenza, ma era anche un moto che non era davvero tale, perché non portava in nessun luogo). Questa geometrizzazione, quindi, tendeva a escludere gli astri dal mondo del cambiamento e ad attribuire loro se non proprio l'immobilità, almeno la regolarità e la perennità che, per la maggior parte dei filosofi greci, si confaceva al divino. Essa eliminava la dinamica che l'aritmetica assicurava invece all'astronomia babilonese, in cui le progressioni davano ai cambiamenti astronomici un ordine numerico che era anche un ordine temporale, una generazione. Nell'astronomia greca lo scopo era quello di capire la struttura del Cosmo, piuttosto che quello di predire l'avvenire; si mirava a ciò che è stabile e permanente sotto l'aspetto mutevole del divenire.
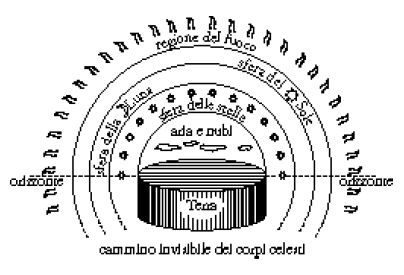
Nella Ionia i filosofi proposero diversi modelli astronomici 'protogeometrizzati'; per esempio, Anassimandro collocava la Terra al centro del mondo, dove si manteneva in equilibrio perché era a uguale distanza da tutte le cose (secondo quanto affermano Ippolito di Roma nei Philosophoumena (I, 6) e Aezio nella sua Raccolta di opinioni filosofiche (Placita, II, XX, 1; II, XXI, 1; II, XXV, 1). Intorno a questa Terra, a cui era attribuita la forma di un cilindro (di altezza pari a un terzo del diametro), ruotavano tre anelli, o 'sfere' (fig. 4): la sfera degli astri fissi, cioè delle stelle (quella più vicina alla Terra), quella della Luna e infine quella del Sole (il diametro di queste sfere era pari, rispettivamente, a 9, 18 e 27 volte il diametro della Terra, proporzioni peraltro non presenti nella figura). Qualunque sia l'autenticità dei particolari riportati dai dossografi, si tratta di un modello astronomico geometrico. L'aritmetica era presente solamente nell'uso del numero 3, in un modo che ricorda le proporzioni più che le progressioni (non interveniva nella previsione della posizione degli astri, ma nella struttura del Cosmo).
Nonostante questa 'protogeometrizzazione' i filosofi ionici avevano una concezione del mondo abbastanza concreta (Anassimandro era certamente il più astratto). I fenomeni astronomici erano ancora più o meno confusi con i processi meteorologici, e nella spiegazione di entrambi si faceva ricorso ad analogie fisiche derivate dall'esperienza corrente.
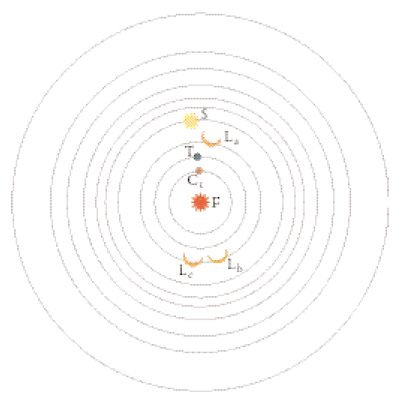
Si ritiene che i veri inventori dell'astronomia geometrica siano stati i pitagorici, e il più noto dei loro modelli astronomici, quello di Filolao di Crotone (fig. 5), ha la particolarità di non essere geocentrico. Sempre secondo quanto scrive Aezio nella Raccolta (II, VII, 7), il centro dell'Universo era occupato da un fuoco, sede della divinità che regolava i moti celesti, e attorno a questo fuoco gravitavano dieci astri (o gruppi di astri): l'Antiterra, la Terra, la Luna, il Sole, Mercurio, Venere, Marte, Giove, Saturno e infine le stelle fisse (per ottenere il numero 10, di cui conosciamo l'importanza per i pitagorici, Filolao fu costretto a inventare un astro immaginario, l'Antiterra). Secondo quanto riporta Plutarco nella sua opera De animae procreatione in Timaeo (XXXI), considerato pari a 1 il diametro del fuoco centrale F, 3 sarebbe stato il diametro dell'orbita dell'Antiterra (Ct), 9 (=3²) il valore corrispondente per la Terra T, 27 (=3³) per la Luna (in varie posizioni: La, Lb, Lc), 81 (=3⁴) per Mercurio, 243 (=3⁵) per Venere, 729 (=3⁶) per il Sole, e così via per Marte, Giove e Saturno. Quest'ordine degli astri non corrisponde a quello riportato da altri dossografi, ma l'essenziale è la natura geometrica di questa astronomia e la rappresentazione intelligibile del Cosmo, e non più l'uso di progressioni aritmetiche per predire il futuro.
L'aritmetica continua a trasparire nei rapporti tra i diametri delle orbite o, in maniera meno 'matematica', nell'invenzione dell'Antiterra che permette di portare a 10 il numero degli astri; inoltre, essa si manifesta nel rapporto tra astronomia e musica. I pitagorici, infatti, attribuivano una struttura matematica alla musica mediante le proporzioni, e questa era senz'altro la parte della loro 'fisica' a cui la matematica si applicava meglio. L'armonia delle sfere non era soltanto l'ordine armonioso del Cosmo; era anche, letteralmente, una musica. Si riteneva (Porfirio e Teone di Smirne) che i corpi in movimento, e quindi gli astri, emettessero un suono, tanto più acuto quanto più il loro moto era rapido; dunque, grazie al rapporto tra diametro dell'orbita e velocità, gli astri avrebbero prodotto una musica. La descrizione di questa armonia astronomica è riferita in modi diversi dalla dossografia ed è abbastanza difficile sapere che cosa fosse esattamente per i pitagorici. Comunque sia, sembra che l'aspetto dinamico dell'astronomia (il moto degli astri) fosse in tal modo ricollegato dalla musica all'aritmetica, mentre la geometria si preoccupava unicamente del disegno delle orbite (quanto c'era di 'fisso' in questo moto).
In linea generale, il confronto tra l'astronomia babilonese e quella greca mostra che in Grecia, ancor prima della scoperta dei numeri irrazionali, nell'applicazione della matematica allo studio della Natura la geometria tendeva a prevalere sull'aritmetica. Parallelamente, la proporzione prendeva il posto della progressione. L'oggetto della progressione era la generazione di un n-esimo termine da parte degli (n‒1) precedenti; la proporzione, invece, riguardava i rapporti tra i termini, e quindi una struttura. L'amore dell'intelligibilità aveva il sopravvento sulla predizione del futuro, il sapere 'puro' sul sapere pratico. Se la Grecia ha derivato da Babilonia alcune conoscenze astronomiche 'positive', le ha dunque riprese in tutt'altro spirito (non parliamo qui dell'astrologia ellenistica).
Medicina egizia e medicina greca
La medicina pone un problema diverso. L'efficacia della terapia predominava sulla spiegazione della malattia e della guarigione, e nell'Antichità queste spiegazioni erano molto vaghe e furono inizialmente debitrici alla mistica e alla magia. Esse fungevano sia da semplici giustificazioni a posteriori di cure empiriche, sia da sostegno a pratiche come gli incantesimi, gli esorcismi o altre terapie magiche. Quando simili spiegazioni furono giudicate insufficienti, si cercò di sviluppare un quadro naturale che rendesse conto della salute, della malattia e dell'azione delle cure, generalmente secondo una modalità analogica; ciò certamente liberò la medicina da alcune pratiche magiche, ma non produsse alcun reale progresso terapeutico.
Una spiegazione naturalistica delle malattie fece la sua comparsa molto prima di Ippocrate: se ne trovano tracce nei documenti mesopotamici e, in modo più netto, nei documenti egizi. In Mesopotamia, nel trattato accadico delle diagnosi e prognosi mediche (VII sec., forse copiato da documenti più antichi), i testi che riguardano unicamente la magia e l'esorcismo sono raggruppati e separati da quelli che hanno un significato medico più esplicito. Questi testi medici, nonostante ricorrano spesso a spiegazioni soprannaturali della malattia (punizione degli dèi, maleficio, 'mano dello spettro'), tuttavia non ignorano le cause naturali ('colpo di polvere', 'febbre da aridità'). Essi attestano un inizio di sistematizzazione nell'esame dei sintomi, oltre che la stesura di una prognosi (guarigione possibile o impossibile) e talvolta anche di una sorta di diagnosi. Per quanto riguarda la terapia, i testi menzionano incantesimi e cure magiche, ma vi si trovano anche cure naturali comparabili con quelle egizie o quelle della collezione ippocratica.
In Egitto, il papiro Ebers (1550 ca.), il più esteso papiro medico che ci sia rimasto, comincia con alcuni incantesimi destinati ad accrescere l'efficacia delle cure, incantesimi ai quali però, in seguito, non fa più cenno, proponendo unicamente cure naturali. Le diverse affezioni prese in considerazione sono classificate secondo le parti del corpo che colpiscono. Come nel caso della Mesopotamia, è difficile precisare quale efficacia potessero avere queste cure; alcune conservano traccia di un'origine magica (molto meno netta che in Mesopotamia), ma altre sono chiaramente ricette empiriche.
In questo campo è decisamente più rilevante il papiro Smith (1650 ca.), che sul recto è esclusivamente consacrato alla chirurgia; esso è infatti molto più sistematico del papiro Ebers. I mali da curare sono classificati secondo le parti del corpo che colpiscono e tutti i casi sono presentati nello stesso modo: nome dell'affezione, esame del paziente, diagnosi, prognosi (in tre forme: 'malattia che curerò', 'che combatterò', 'che non curerò'), cura, commento. Inoltre, le cure dovevano avere una certa efficacia, almeno in quanto non comportavano operazioni nefaste.
Rispetto alla medicina, la chirurgia egizia sembra dunque essersi inoltrata di più sulla strada della 'naturalizzazione' e della razionalizzazione. Ciò deve essere derivato dal fatto che le operazioni chirurgiche (riduzione di fratture, di lussazioni, e così via) avevano un aspetto meccanico che ne facilitava l'intelligibilità, mentre le droghe usate dalla medicina agivano in modo misterioso. In linea generale le azioni meccaniche dell'uomo (compiute, per es., mediante la ruota, la carrucola o la leva, oppure la filatura, la tessitura, l'architettura o la chirurgia) sfuggivano più facilmente alla magia rispetto alle azioni non meccaniche, sia che si trattasse della fabbricazione di vasi o della metallurgia primitiva (l'azione del fuoco sulla Terra, sui minerali e sui metalli era considerata magica), sia che si trattasse di tecniche chimiche (fabbricazione dei colori, del vetro, e così via), o, infine, di droghe medicinali. Per la medicina e la chirurgia dell'Antichità l'empirismo era l'unico mezzo per acquisire una certa efficacia ma, nel caso della chirurgia, quest'empirismo era rafforzato da un'intelligibilità che mancava alla medicina. Di qui lo sviluppo precoce di una chirurgia più efficace della medicina.
Il papiro Smith, così come quello Ebers, non può che essere il risultato di una lunga pratica, accompagnata dalla registrazione sistematica delle osservazioni; d'altra parte, la letteratura antica evoca frequentemente l'eccellenza della medicina egizia. Erodoto sostiene nelle Storie (II, 84) che i medici erano specializzati, chi nelle malattie degli occhi, chi in quelle del ventre, e così via. Strabone, a sua volta, nella Geographia (XVII), afferma che gli Egizi erano soliti annotare la descrizione delle malattie e delle cure in registri che venivano conservati nei templi. Diodoro Siculo, nella Bibliotheca (I, 82), aggiunge che i medici avevano l'obbligo di seguire le prescrizioni annotate in questi registri. Tutte queste testimonianze depongono a favore di un empirismo medico. Uno sviluppo simile si ritrova nella medicina greca, originariamente legata ai templi; Strabone afferma infatti che Ippocrate studiò "le storie delle cure che erano depositate nel tempio di Coo" (Geographia, XIV, 2, 19). La collezione ippocratica, tuttavia, va oltre il semplice empirismo, definendo salute e malattia all'interno della teoria degli umori. Questa teoria contiene un abbozzo di fisiologia, in cui il corpo è composto da quattro umori (sangue, flegma, bile gialla e bile nera). La salute risulta dall'equilibrio, dalla giusta proporzione e dalla commistione degli umori; la malattia dal loro squilibrio. Questa fisiologia, quindi, conferisce alla malattia una 'naturalità' che va oltre il riconoscerne la causa in questo o quel fattore naturale (climatico o alimentare). La fisiologia umorale non aveva, naturalmente, alcun impatto sull'efficacia delle cure, e tuttavia trasformava lo spirito della medicina, i cui metodi esplicativi si avvicinavano alla fisica sviluppatasi nella Ionia un po' prima di Ippocrate.
Lontani dalle tendenze matematiche pitagoriche elaborate nella Magna Grecia gli Ionici, infatti, cercarono di creare una fisica che facesse di un elemento (l'acqua per Talete, l'aria per Anassimene) l'origine e il sostrato di tutte le cose, mirando quindi a una 'naturalizzazione' della spiegazione. Questa naturalizzazione era probabilmente collegata al mito (per es., a quello di Oceano, nel caso di Talete), ma ricorreva soprattutto ad analogie con l'esperienza comune (l'acqua che evapora si trasforma in aria e durante l'evaporazione può lasciare un deposito minerale, trasformandosi in pietra). Ciò non bastava a fare una scienza, e tuttavia 'laicizzava', per così dire, la spiegazione, tendendo a liberarla dalla magia. La concezione della salute come equilibrio (o proporzione) derivava dal pitagorismo (la si attribuisce ad Alcmeone), ma la naturalità introdotta dagli umori derivava probabilmente dai fisici ionici.
Per quanto riguarda l'Egitto non si conosce nulla di simile, né, a fortiori, per Babilonia; tuttavia nel papiro Ebers si osserva un abbozzo di spiegazione delle malattie nell'ambito di una fisiologia, e questa spiegazione non manca di ricordare alcuni elementi che saranno presenti, molto più tardi, nella collezione ippocratica.
Il papiro Ebers, per esempio, indica la causa della sincope nel fatto che "il cuore non parla più", e quella dello svenimento nel fatto che i vasi trasportano delle scorie. Ora, nella collezione ippocratica, il trattato De morbo sacro afferma che l'epilessia insorge nei flegmatici perché, in questi individui, il flegma può ostruire i vasi che veicolano l'aria, nella fattispecie verso il cervello (di qui la perdita di conoscenza, dato che in questo trattato si ritiene che l'aria, tradizionalmente vivificante, produca nel cervello il pensiero). È difficile non stabilire un rapporto con la spiegazione egizia, anche se non si può veramente precisare se vi sia stato prestito o invece convergenza; d'altronde non è questa la cosa più importante: l'essenziale è che l'Egitto sembra aver delineato una spiegazione delle malattie nell'ambito di una fisiologia, anche se questa fisiologia era molto embrionale e, apparentemente, non si accompagnava a una fisica comparabile con quella degli Ionici.
Dalle scienze 'barbare' alla scienza greca
Ai suoi albori la scienza greca era caratterizzata da una doppia corrente: da una parte la naturalizzazione della spiegazione ‒ in atto nella fisica ionica e nella medicina ippocratica ‒ la cui principale modalità era l'analogia, e, dall'altra parte, il matematismo pitagorico, o di ispirazione pitagorica, che al tempo stesso comprendeva la ricerca di dimostrazioni in campo matematico, la loro articolazione in un corpus unitario (gli Elementi, a cui Euclide darà forma definitiva) e il tentativo di coinvolgere la matematica nell'indagine delle scienze naturali, ossia una spiegazione che privilegiava l'intelligibilità matematica e non più l'analogia. Se la naturalizzazione della spiegazione ha forse avuto alcuni precedenti in Mesopotamia e in Egitto, almeno nel caso della medicina, l'intelligibilità matematica sembra propriamente greca; la matematica mesopotamica ed egizia, e l'astronomia babilonese si preoccupano infatti più delle procedure che dell'intelligibilità.
Paradossalmente, però, la naturalizzazione ionica lasciava insoluto il problema della Natura e delle sue forze. Essa spiegava fenomeni inaccessibili all'uomo riducendoli, per mezzo di analogie, a processi fisici che erano alla sua portata (in tal modo la luce degli astri era ricondotta a una combustione); ma questi processi fisici familiari all'uomo non erano veramente studiati in quanto tali, in sé stessi e servivano semplicemente da supporto alle analogie; così, per sostenere, ad esempio, che il Sole è una pietra incandescente lo 'naturalizza' mettendolo in rapporto con la pietra che si mette a scaldare nel fuoco, ma non lo spiega, proprio come non spiega la pietra e il fuoco. Più che spiegarlo veramente, questa naturalizzazione dunque smitizzava il mondo. Essa rendeva possibile una spiegazione scientifica liberando i fenomeni dall'autorità del mito, ma poteva anche far richiudere la spiegazione su sé stessa, nella misura in cui l'analogia veniva giudicata sufficiente. Quindi la fisica ionica e la medicina ippocratica, per quanto gloriose, furono strade senza uscita; per lo sviluppo successivo della scienza greca questa corrente fu meno importante e meno feconda di quella che privilegiava l'intelligibilità matematica.
Per spiegare il passaggio dalla scienza 'barbara' alla scienza greca spesso sono evocati tre avvenimenti che hanno avuto luogo, più o meno nello stesso periodo, nel mondo greco o ai suoi confini. Il primo è l'invenzione dell'alfabeto (prima si conoscevano solamente scritture consonantiche, sillabiche o, più frequentemente, miste, cioè ideografiche e fonetiche insieme); il secondo è l'invenzione della moneta, nella Lidia di Creso; il terzo è la democrazia, senza dubbio il fattore più importante, quello dalle conseguenze più vaste.
Generalmente la filosofia e la scienza sono messe in relazione con l'abitudine democratica di sottoporre ogni questione al discorso critico dei cittadini. Nella pólis greca la partecipazione alla vita sociale era 'regolata' attraverso le leggi che gli uomini si davano, mentre negli imperi egizi o mesopotamici questa partecipazione era vissuta come una sottomissione a leggi che si ritenevano divine.
In Egitto il faraone era divinizzato e il clero era politicamente attivo. La Mesopotamia era meno teocratica (soprattutto nel suo periodo più tardo); il più antico codice noto, tuttavia, quello di Hammurabi, precisa nel suo epilogo: "Hammurabi, re della giustizia, a me Shamash ha fatto dono delle leggi" (col. XXV, 95-98). Poiché Shamash era il dio del Sole, le leggi erano di origine divina. Anche nella Grecia arcaica si riteneva che il re, il cui ruolo era religioso, ricevesse il proprio potere dagli dèi; tale concezione, però, sparì nelle pólis della Grecia classica.
Mentre in Egitto e in Mesopotamia chi deteneva il potere governava per mezzo di leggi senza essere a sua volta governato (se non dagli dèi da cui riceveva le leggi), in Grecia era anche lui soggetto alle leggi e poteva governare soltanto rispettandole a sua volta. I rapporti tra i cittadini e il potere politico che passavano attraverso queste leggi, grazie a esse erano percepiti come 'razionali', mentre in Egitto e in Mesopotamia i rapporti tra i sudditi e il monarca non erano considerati razionali ma vissuti sotto l'avallo del mito che affermava la divinità del monarca. Lo stesso valeva per i rapporti tra gli individui; negli imperi antichi questi rapporti passavano infatti attraverso un'organizzazione sociale (caste, classi, e così via) avallata in modo mitico, mentre in Grecia erano razionalizzati attraverso leggi (o situazioni economiche, di cui queste leggi potevano tener conto).
Negli imperi antichi l'ordine politico e sociale, che dipendeva da quello divino, non differiva dall'ordine della Natura, che procedeva ugualmente dagli dèi; c'era, se non proprio una continuità, per lo meno un'interferenza tra Natura, società e divinità. Nella democrazia greca, invece, l'ordine politico e sociale era un ordine umano, che, affrancandosi dal divino, si affrancava anche dalla Natura. La sfera politica e sociale si separava così dalla sfera naturale e divina; la vita politica nella pólis, dunque, conferiva all'uomo un'autonomia nei confronti della natura e degli dèi.
Proprio per dare dei principî e una struttura a questa autonomia interveniva il discorso critico dei cittadini e quindi il linguaggio. Attraverso il linguaggio, infatti, l'uomo cercava di esprimere la propria esperienza di sé e del mondo, sia per comunicarla agli altri sia per conservarla nel proprio intimo. Certo, il primo linguaggio non somigliava minimamente a quello studiato dai linguisti di oggi, con i suoi significanti, i suoi significati e la sua sintassi. Il suo valore dipendeva dalla sua capacità espressiva, la quale ultima evocava però l'esperienza vissuta più che esplicitarla in un ambito grammaticale molto rigoroso; una capacità espressiva, quindi, comparabile a quella della poesia (antica quanto il linguaggio) o a quella del mito, la cui efficacia dipendeva più dall'evocazione e dall'analogia che dalla spiegazione razionale. Si potrebbe dire che questo primo linguaggio stia al linguaggio dei linguisti come la scrittura ideografica alla scrittura alfabetica. La scrittura ideografica, infatti, aderisce alla realtà che vuole esprimere; essa ha un valore espressivo immediato e poco grammaticale, mentre l'espressività della scrittura alfabetica è mediata, passa attraverso una convenzione e necessita di una grammatica più rigorosa. Come nella scrittura ideografica, dunque, in questo primo linguaggio quel che si voleva esprimere prevaleva sul modo in cui l'espressione prendeva forma; il segno era subordinato al senso, e il senso travalicava il segno. Nella scrittura alfabetica e nel linguaggio evoluto, invece, il segno prevale: quel che si vuole esprimere deve, in un modo o in un altro, introdursi nella forma codificata dell'espressione.
Questo primo linguaggio non separava l'uomo e il mondo; la grammatica non si frapponeva tra loro facendo percepire il mondo attraverso una rappresentazione fatta di significati articolati secondo la sintassi che regola i significanti. Invece di essere associate per semplice convenzione, la parola e la cosa erano congiunte da un intimo rapporto, e questa intimità prevaleva sul formalismo grammaticale. Questo linguaggio originario conservava dunque una fortissima aderenza alla realtà di cui cercava di rendere conto ma, al contempo, se ne differenziava ed esercitava su quella realtà una virtù magica: quella che agiva negli incantesimi, nelle benedizioni e nelle maledizioni, e in base alla quale conoscere il nome di una persona o di una cosa conferiva un potere su questa. Questa magia della parola era alla base della fede nel potere creatore della parola divina, fede diffusa fin dall'Alta Antichità in Mesopotamia, nel Vicino Oriente e in Egitto. Per questo linguaggio si poneva un problema di livello di esistenza simile a quello dei numeri: la parola non aveva lo stesso livello di esistenza di ciò che designava, eppure vi era sufficientemente legata da avere potere su di esso (con la differenza che in generale la parola doveva essere proferita per esercitare il proprio potere, cosa invece non necessaria al numero, dotato di una virtù più 'strutturale').
Col passare del tempo questo aspetto magico è regredito e il linguaggio si è avvicinato a quello che oggi conosciamo, che impone la propria forma alla rappresentazione del mondo e che, con la sua standardizzazione, facilita la comunicazione con gli altri. L'espressione grammaticale si è sviluppata a detrimento dell'espressività in atto nella poesia e nel mito, frapponendo la sua griglia di lettura tra l'uomo e il mondo. La grammatica, infatti, dà forma all'esperienza che l'uomo fa del mondo, e tale esperienza tende a essere pensata 'grammaticalmente', più che a essere vissuta in modo immediato. Il linguaggio acquisisce così un'autonomia nei confronti di quel che tenta di esprimere, aderendovi sempre meno. Frapposto com'è tra l'uomo e il mondo, il linguaggio non appartiene più veramente né all'uno né all'altro. Separato dal mondo, esso tende a perdere il proprio potere magico; ormai parole e cose sono unite soltanto da una convenzione; incantesimi, benedizioni e maledizioni regrediscono. Separato dall'uomo, il linguaggio tende a funzionare in modo indipendente: da un lato non è più subordinato all'esperienza vissuta, bensì la sottopone ai vincoli della grammatica; dall'altro lato diventa, per così dire, 'bulimico' e passa al vaglio ogni cosa.
Quest'autonomia del linguaggio può essere messa a confronto con quella della moneta, la terza delle invenzioni che sono abitualmente messe in rapporto con la filosofia e la scienza. Anche la moneta si frappone tra l'uomo e il mondo, e alla percezione immediata degli oggetti, della loro utilità e del loro valore simbolico (nel consumo o nel baratto); essa sostituisce un sistema a due facce, quello della merce che ha valore d'uso e valore di scambio (Baudrillard 1972). Si tratta anche in questo caso di un sistema che tende a diventare autonomo e a funzionare da sé e per sé.
Il linguaggio va però collegato soprattutto al potere politico: infatti l'espressività immediata, scarsamente grammaticale, del primo linguaggio era parallela al modo in cui negli imperi antichi era vissuta la partecipazione alla società, ossia un modo immediato e non elaborato razionalmente attraverso una costituzione (una 'grammatica politica' che frapponesse un ordine sociale tra l'uomo e il mondo). Nello stesso modo il linguaggio 'grammaticale' può essere messo in rapporto con la democrazia greca. È probabile infatti che nella democrazia la necessità di elaborare razionalmente la propria posizione sociale all'interno di un ordine politico autonomo abbia indotto gli uomini a vedere il mondo come un 'cosmo' (un ordine) e a pensare il loro posto nel mondo in forma discorsiva, privilegiando l'intelligibilità a discapito dell'espressività immediata della poesia e del mito.
Quest'evoluzione del linguaggio era certamente cominciata molto prima, ma è stata consacrata dalla democrazia, che ha fatto della discorsività intelligibile un ideale. L'autonomia del linguaggio, il dominio della grammatica e la regressione dell'adesione magica al reale, risultano così strutturalmente legate a questo sistema politico. Nella democrazia l'unico potere che il linguaggio ancora conserva è quello della persuasione per mezzo del discorso, secondo quanto afferma Gorgia di Leontini nell'Encomio di Elena (DK 82 B 11). Ma la persuasione non è la verità e questo linguaggio autonomo, poiché non è accompagnato da un'aderenza al reale, volge alla sofistica, un'ebbrezza linguistica che pretende di dimostrare qualsiasi cosa. Dunque l'autonomia del linguaggio non basta: bisogna strutturarla e dotarla di principî, così come bisogna fare in ambito politico (dove alla sofistica corrisponde la demagogia).
A questo miravano, per esempio, Platone e Aristotele, proponendo il primo una dialettica e l'altro una logica, nel tentativo di dare ordine proprio al pensiero discorsivo nato dall'emergere di un linguaggio grammaticale autonomo, a discapito del linguaggio della poesia e del mito. Ma cosa c'era alla base di questo tentativo di razionalizzazione?
L'agitata vita politica delle póleis greche e la tendenza a sottoporre ogni cosa al discorso critico dei cittadini hanno certamente contribuito a mettere ordine nel pensiero, di qualunque genere esso fosse: politico, filosofico o scientifico. Ma è probabilmente intervenuto anche un altro fattore, cioè la matematica come modello della vera conoscenza. La ricerca dell'intelligibilità, inerente alla democrazia, non poteva che favorire, di fatto, lo sviluppo della matematica. Così numeri e figure sono stati considerati oggetti matematici in sé stessi, come un mondo autonomo con caratteri e metodi propri. La natura di questi oggetti matematici era mal definita; il loro livello di esistenza, situato da Platone tra il mondo sensibile e il mondo delle idee, era altrettanto difficile da precisare di quello del linguaggio. Essi godevano però di una struttura molto più evidente, rigorosa e unitaria di quella che la grammatica poteva dare al linguaggio (come è evidente nell'esempio della somma dei numeri dispari successivi precedentemente fornito). La proprietà aritmetica si mostrava da sé, con la stessa chiarezza con cui si rendeva evidente allo schiavo del Menone (82 a - 86 b) di Platone la geometria della duplicazione del quadrato. Questa struttura unitaria e rigorosa servì da modello per la conoscenza, un modello che Platone pretese persino di superare con la sua dialettica che relegava la matematica al rango di propedeutica. I filosofi, e Platone in particolare, hanno certamente contribuito a chiarificare il procedimento matematico, ma lo hanno anche preso come esempio per cercare di costruire un modo di pensare che fosse altrettanto rigoroso sebbene comprendesse un terreno più vasto (che va dalla politica alle scienze naturali, passando dalla morale).
Così, mentre la Mesopotamia e l'Egitto accumularono varie conoscenze fattuali (matematiche, astronomiche e mediche) ‒ tanto in vista di applicazioni pratiche (agricoltura, commercio, calendario, e così via), quanto in un ambito mistico (astrologia, magia delle parole e dei numeri) ‒ ma senza che l'intelligibilità fosse mai eretta a criterio di verità, in Grecia la democrazia delle póleis favorì l'autonomia del linguaggio, la rottura dei suoi legami magici col reale e il predominio della grammatica, vale a dire il progresso di un pensiero discorsivo che privilegiava l'intelligibilità ma che si perdeva talvolta nella sofistica in cui la persuasione sostituiva la verità. Nello stesso senso ciò favorì lo sviluppo di un genere particolare di discorsività, il ragionamento matematico, il cui mondo era autonomo quanto quello del linguaggio, ma meglio costruito; ciò gli conferiva un rigore e un'intelligibilità molto superiori alle tecniche linguistiche di persuasione. Così, la matematica divenne il modello, all'interno della dialettica platonica o della logica aristotelica, per disciplinare l'autonomia del linguaggio grammaticale fuorviatasi nella sofistica; questo è probabilmente alla base della filosofia greca, ma anche della scienza greca. Quest'ultima ha certamente derivato alcune conoscenze fattuali dalla Mesopotamia e dall'Egitto, riformulandole però nello spirito che le era proprio, e ad assicurare il suo sviluppo e la sua perennità furono meno quei prestiti, per quanto utili, che quello spirito.
Bibliografia
Baudrillard 1972: Baudrillard, Jean, Pour une critique de l’économie politique du signe, Paris, Gallimard, 1972.
Bottéro 1952: Bottéro, Jean, La religion babylonienne, Paris, Presses Universitaires de France, 1952.
Burnet 1892: Burnet, John, Early Greek philosophy, London, A. & C. Black, 1892 (4. ed.: 1952).
Caveing 1994-97: Caveing, Maurice, La constitution du type mathématique de l’idéalité dans la pensée grecque, Lille, Presses Universitaires de Lille, 1994-1997, 2 v.
Chace 1927-29: The Rhind mathematical papyrus, British museum 10057 and 10058, photographic facsimile, hieroglyphic transcription, transliteration, literal translation, free translation, mathematical commentary, and bibliography, edited by A.B. Chace, L. Bull, Oberlin (Ohio), Mathematical association of America, 1927-1929, 2 v.
Contenau 1938: Contenau, Georges, La médecine en Assyrie et en Babylonie, Paris, Maloine, 1938.
– 1940: Contenau, Georges, La divination chez les Assyriens et les Babyloniens, Paris, Payot, 1940.
Duhem 1954: Duhem, Pierre Maurice Marie, Le système du monde. His - toire des doctrines cosmologiques de Platon à Copernic, Paris, A. Hermann, 1913-1959, 10 v.; v. I, 1954.
Dumont 1988: Les Présocratiques, édition établie par Jean-Paul Dumont, Paris, Gallimard, 1988.
Ellul 1961: Ellul, Jacques, Histoire des institutions de l’antiquité, nouvelle éd., Paris, Presses Universitaires de France, 1961.
Février 1959: Février, James Germain, Histoire de l’écriture, nouv. éd. entièrement refondue, Paris, Payot, 1959 (1. ed.: 1948).
Finley 1970: Finley, Moses I., Early Greece. The bronze and archaic ages, London, Chatto & Windus, 1970.
Gaudemet 1967: Gaudemet, Jean, Institutions de l’antiquité, Paris, Sirey, 1967.
Goody 1977: Goody, Jack, The domestication of the savage mind, Cambridge-New York, Cambridge University Press, 1977.
– 1986: Goody, Jack, Logic of writing and the organization of society, Cambridge-New York, Cambridge University Press, 1986.
Guitel 1975: Guitel, Geneviève, Histoire comparée des numérations écrites, Paris, Flammarion, 1975.
Heath 1949: Heath, Thomas Little, Mathematics in Aristotle, Oxford, Clarendon Press, 1949 (rist.: Mathematics in Aristotle, New York, Garland Publ., 1980).
Ifrah 1994: Ifrah, Georges, Histoire universelle des chiffres. L’intelligence des hommes racontée par les nombres et le calcul, Paris, R. Laffont, 1994.
Kramer 1956: Kramer, Samuel Noah, From the tablets of Sumer; twentyfive firsts in man’s recorded history, Indian Hills (Col.), Falcon’s Wing Press, 1956.
Labat 1951: Traité akkadien des diagnostics et pronostics médicaux, édité par René Labat, Paris, Académie internationale d’histoire des sciences, 1951, 2 v.
Lloyd 1970: Lloyd, Geoffrey Ernest Richard, Early Greek science: Thales to Aristotle, London, Chatto & Windus, 1970.
– 1973: Lloyd, Geoffrey Ernest Richard, Greek science after Aristotle, London, Chatto & Windus, 1973.
– 1979: Lloyd, Geoffrey Ernest Richard, Magic, reason, and experience: studies in the origin and development of Greek science, Cambridge-New York, Cambridge University Press, 1979 (trad. it.: Magia, ragione, esperienza. Nascita e forme della scienza greca, Torino, Boringhieri, 1982).
Michel 1950: Michel, Paul-Henri, De Pythagore à Euclide. Contribution à l’histoire des mathématiques préeuclidiennes, Paris, Les Belles Lettres, 1950.
Morenz 1960: Morenz, Siegfried, Ägyptische Religion, Stuttgart, Kohlhammer, 1960 (trad. it.: La religione egizia, Milano, Il Saggiatore, 1968).
Neugebauer 1951: Neugebauer, Otto, The exact sciences in antiquity, Copenhagen, E. Munksgaard, 1951 (2. ed.: Providence, Brown University Press, 1957) (trad. it.: Le scienze esatte nell’antichità, Milano, Feltrinelli, 1974).
– 1955: Neugebauer, Otto, Astronomical cuneiform texts. Babylonian ephemerides of the Seleucid period for the motion of the sun, the moon and the planets, London, Published for the Institute for Advanced Study, Princeton (N.J.), by Lund Humphries, 1955, 3 v.
Pichot 1991: Pichot, André, La naissance de la science, Paris, Gallimard, 1991, 2 v. (trad. it.: La nascita della scienza. Mesopotamia, Egitto, Grecia antica, Bari, Dedalo, 1993).
Rey 1930-48: Rey, Abel, La science dans l’antiquité, Paris, La Renaissance du livre, 1930-1948, 5 v.
Robin 1973: Robin, Léon, La pensée grecque et les origines de l’esprit scientifique, Paris, A. Michel, 1973.
Vernant 1962: Vernant, Jean-Pierre, Les origines de la pensée grecque, Paris, Presses Universitaires de France, 1962 (4. ed.: 1981).
– 1965: Vernant, Jean-Pierre, Mythe et pensée chez les Grecs. Études de psychologie historique, Paris, F. Maspero, 1965 (trad. it.: Mito e pensiero presso i Greci. Studi di psicologia storica, Torino, Einaudi, 1970).