Scienza greco-romana. Archimede
Scienza greco-romana. Archimede
Archimede
Archimede è l’unico dei matematici greci di cui abbiamo notizie storiche; questa eccezionalità è dovuta in parte ai risultati da lui ottenuti, in parte ai casi della sua vita e del suo tempo. Non abbiamo notizie di un’attività politica di Archimede altrettanto intensa quanto quella di altre figure, come Archita o Eudosso; la sua fama al di fuori della matematica risale all’assedio da parte dei Romani della sua città natale, Siracusa, durante la Seconda guerra punica, negli anni 214- 212. Eccone la versione di Tito Livio nella sua storia di Roma:
E in effetti l’impresa iniziata con così grande impeto avrebbe avuto successo, se soltanto a Siracusa non ci fosse stato, in quel tempo, un uomo, Archimede. Egli era un impareggiabile osservatore del cielo e delle stelle, un ancor più straordinario, nondimeno, scopritore e costruttore di congegni e di macchine da guerra, con cui era in grado di prendersi gioco con il minimo sforzo di [qualsiasi azione] fosse con enorme impiego di forze dai nemici condotta. (Ab urbe condita libri, XXIV, 34)
Nel 212 la città, caduta probabilmente per tradimento, fu saccheggiata dai soldati romani:
si narra che mentre venivano dati molti disgustosi esempi di furore e di cupidigia, Archimede, il quale – pur nell’enorme scompiglio quale poteva essere quello suscitato [dal panico] della città invasa, in mezzo al correre qua e là dei soldati intenti al saccheggio – era tutto preso da figure geometriche che aveva tracciato sulla sabbia, fu ucciso da un soldato che ignorava chi egli fosse; [e si narra che] Marcello provò dispiacere per questo, e ci si prese cura del funerale, e il nome e il ricordo di lui furono di onore e di protezione per i suoi parenti, che furono fatti ricercare. (ibidem, XXV, 31)
Molti storici antichi narrano questi eventi, tra cui Polibio, che è molto affidabile. Queste testimonianze ci consentono di dedurre alcune cose. In primo luogo, Archimede deve essere morto nel 212, probabilmente vecchio; quindi le date della sua vita sono molto più sicure di quelle di altri matematici dell’Antichità. In secondo luogo, oltre che matematico e studioso egli era anche ingegnere e fu certamente uno dei capi della difesa di Siracusa. In terzo luogo, già all’epoca di Tito Livio, se non prima, era considerato un eroe da Greci e Romani, anche se per ragioni diverse (Tito Livio se ne serve per esaltare Marcello). Infine, cosa molto importante, era una leggenda e, dunque, non bisogna fidarsi troppo delle storie che lo riguardano. Archimede è realmente esistito e partecipò a una battaglia della guerra tra Roma e Cartagine; tuttavia, le fonti parlano di Archimede non soltanto come figura storica, ma anche come figura utilizzata in guerre ideologiche: tra Romani e Greci, oltre che tra ‘scienza pura’ o ‘filosofia’ e ‘meccanica’. Per la storia intellettuale, la disputa più importante è quella tra scienza pura e ‘scienza applicata’; cercheremo dunque di approfondire questo problema storiografico, senza però poter dire una parola definitiva, a causa proprio dell’aspetto ideologico delle testimonianze che abbiamo. Considereremo quindi la persona di Archimede cercando al contempo di definirne la personalità scientifica. Le sue opere hanno un’impronta molto caratteristica; anche se scritte in un idioma matematico impersonale, sono in realtà molto ‘archimedee’, ossia molto personali, e cercheremo di cogliere questa loro peculiarità.
La posizione di Archimede riguardo alla questione della separazione tra scienza pura e scienza applicata è molto particolare e difficile da definire. Occorre prima di tutto dire qualcosa sulle condizioni storiche e chiarire se egli fu in effetti il maestro d’arte che costruisce macchine o il filosofo aristocratico immerso nelle proprie figure tanto da non sentire lo strepito dei soldati in battaglia. Non sorprende che le testimonianze sulla sua collocazione sociale siano ambigue: alcune ne fanno un aristocratico, apparentato con la famiglia reale di Siracusa, altre un uomo che si è fatto da sé e dalle oscure origini, e queste contraddizioni favoriscono le leggende. Se è vero che dedicò l’Arenario al re Gelone, i termini della dedica non rivelano quali fossero le relazioni tra i due. Si potrebbe fare maggior chiarezza sul suo status guardando non direttamente ad Archimede, bensì a suo padre, del quale sappiamo due cose grazie a una citazione, anch’essa dell’Arenario, che molto probabilmente si riferisce a lui: il padre dette almeno un contributo all’astronomia teorica e si chiamava Fidia. Il nome non è senza significato; come si verifica infatti in casi analoghi, portare il nome del più grande artista dell’Antichità suggerisce l’appartenenza a una categoria di maestri d’arte, ed è probabile quindi che questo fosse il caso del nonno di Archimede. Una famiglia straordinaria, dunque: un maestro d’arte, il figlio astronomo e soltanto due generazioni dopo il nipote scienziato e, forse, amico del re. Comunque, tutti questi elementi mettono in luce le molte ambiguità che la definizione di una collocazione sociale comporta. D’altra parte, ‘maestro d’arte’ o ‘ingegnere’ non è poi così diverso da ‘artista’, e questo potrebbe essere un modo per risolvere l’opposizione fra scienza pura e scienza applicata. Nella descrizione dei risultati matematici da lui ottenuti vedremo l’Archimede artista, l’artefice di eccezionali opere intellettuali.
Ci è pervenuto un corpus notevole di queste opere, che può essere diviso in quattro gruppi. Il primo gruppo di lavori riguarda il cerchio e la sfera, gli oggetti più affascinanti ma anche tra i più difficili della matematica greca. Su entrambi Archimede ci ha lasciato la trattazione definitiva; infatti, i matematici dell’Antichità menzionano Archimede soprattutto per questo suo contributo, che consiste almeno di tre opere: due sulla sfera, di cui una (Della sfera e del cilindro, Libro I) sulla misura della sfera, un’altra (Della sfera e del cilindro, Libro II) sulla risoluzione di problemi riguardanti la sfera, e una terza dal titolo Sulla misura del cerchio, autoesplicantesi. In queste tre opere egli determinò la migliore misura lineare possibile per gli oggetti curvi più importanti, abolendo la separazione tra enti rettilinei ed enti curvi. Un secondo gruppo di opere è costituito dai lavori dedicati alla ‘matematica della meccanica’, nel senso che trattano oggetti fisici dal punto di vista matematico, oppure oggetti matematici dal punto di vista della meccanica: in questo modo Archimede attraversò un’altra linea divisoria, quella tra matematica e fisica. Vi sono peraltro altre frontiere che furono da lui superate, nel cercare nuovi oggetti geometrici; due suoi trattati, tra i più avanzati della matematica premoderna, Conoidi e sferoidi e Sulle spirali, sono dedicati appunto a ‘strani’ oggetti di un nuovo tipo e alle loro misure, e questi possono essere considerati le opere del terzo gruppo. Infine, se una tale separazione ha senso nelle scienze, Archimede abolì anche la separazione tra il serio e il dilettevole, come mostra il quarto gruppo di opere: due piccoli trattati intitolati Stomachion e Il problema dei buoi, i quali riguardano problemi di matematica ricreativa, e un altro trattato, intitolato l’Arenario, che, pur presentando un tentativo giocoso di calcolare il numero di granelli di sabbia necessari per riempire l’Universo, sviluppa tecniche matematiche altamente sofisticate.
Questi quattordici trattati, che ci sono pervenuti quasi interamente, formano una parte importante dell’opera originale di Archimede. Vi sono fonti arabe che gli attribuiscono anche altre opere e alcune di queste attribuzioni appaiono convincenti (per es., quella di un trattato sui cerchi mutuamente tangenti, pubblicato in appendice all’edizione delle opere di Archimede pubblicata a cura di J.L. Heiberg nella Bibliotheca Scriptorum Graecorum et Romanorum Teubneriana). Queste attribuzioni rendono la figura di Archimede ancora più complessa di quanto non lo sia già quella che emerge dalle fonti greche.
La sfera e il cerchio
Negli studi di Ippocrate di Chio sulla quadratura delle lunule, il più antico esempio di matematica greca attestato, è già presente il problema del cerchio (v. cap. XVI). Ippocrate dimostra come alcune superfici comprese tra linee curve sono uguali ad altre comprese tra rette (possiamo quindi parlare di ‘quadratura’, cioè di ‘misura’, di curve). Le motivazioni che lo spingevano non sono chiare, in quanto non sappiamo se egli avesse di mira la misura del cerchio, anche se per via indiretta, o se volesse misurare proprio le lunule. Un’analoga ambiguità si ritrova in Archimede. Molta parte della sua opera è dedicata alla misura di oggetti curvi e, anche in questo caso, ci possiamo chiedere se egli fosse interessato a una generalizzazione del problema della misura del cerchio ad altri problemi a esso collegati, o se invece sperasse di poter affrontare per questa via il problema del cerchio; non siamo in grado, però, di rispondere a questa domanda.
Archimede andava certamente orgoglioso di una misura in particolare, quella relativa alla sfera: un’iscrizione sulla sua tomba mostrava proprio questa misura con l’ausilio di una figura. Tutte le altre misure, come quelle relative a parabole, conoidi, sferoidi e spirali, riguardavano oggetti in un certo senso artificiali, mentre il cerchio e la sfera avevano un significato particolare, matematico e filosofico, legato al ruolo di queste figure nelle cosmologie dell’Antichità. In merito a entrambe Archimede fece il massimo progresso possibile per i suoi tempi e, poiché per la sfera poté dire di più che per altri oggetti, ai suoi occhi questo contributo fu proprio il suo maggior successo. Vediamo in dettaglio la struttura logica di questo risultato, che è la chiave per capire molti altri risultati di Archimede.
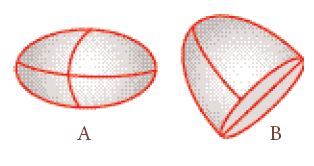
Intanto, a rigore, egli non ‘misurò’ la sfera, nel senso che non la ridusse a oggetti rettilinei ma a oggetti curvilinei più semplici. Più precisamente, nel Libro I dell’opera Della sfera e del cilindro dimostrò che l’area della superficie della sfera è quattro volte quella di un cerchio massimo, per esempio l’equatore (prop. 33); e che il volume della sfera è quattro volte quello di un cono che ha per base un cerchio massimo e per altezza il raggio (prop. 34; fig. 1). La superficie della sfera è un oggetto bidimensionale che si trova immerso in uno spazio a tre dimensioni e in nessun punto è planare. Il fatto che sia uguale a un semplice oggetto bidimensionale – quattro volte un cerchio massimo – è una sorta di riduzione della dimensione della curvatura: se le superfici delle sfere si possono ridurre a cerchi, il mondo risulta in un certo senso meno curvo. Ciò che rende ancor più soddisfacente questa riduzione è che l’oggetto da ridurre, la sfera e quello a cui esso viene ridotto, il cerchio, sono presenti l’uno nell’altra, e per di più la relazione numerica che intercorre tra loro è estremamente semplice.
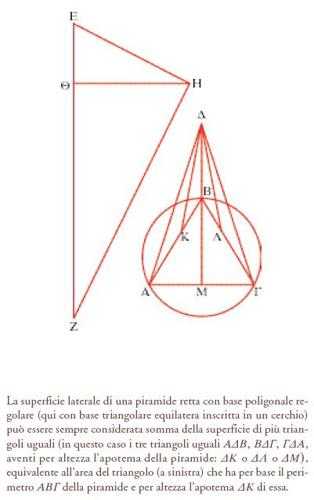
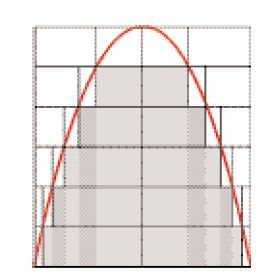
Questi risultati sono dimostrati applicando due idee tra loro collegate: la decomposizione e lo ‘schiacciamento’ o compressione (Dijksterhuis 1938, ed. it. 1989, pp. 130-132). Si comincia con la decomposizione, la superficie laterale di una piramide a base equilatera si pensa costituita da una serie di triangoli uguali tra loro; si decompone cioè la piramide in triangoli (propp. 7-12) e ciò rende la superficie facilmente misurabile (la prop. 8 stabilisce che la sua misura è uguale a quella di un triangolo che ha per base il perimetro della base della piramide e per altezza il lato del cono circolare retto inscritto: fig. 2). Archimede dimostra poi, per esempio, che l’area di questa superficie è maggiore di quella del cono inscritto e minore di quella del cono circoscritto, e ciò mediante una dimostrazione caso per caso, per ciascun triangolo (fig. 3); diversi risultati di questo genere sono enunciati dopo la prop. 12. In generale, quindi, la decomposizione è un modo di ridurre un oggetto complesso a suoi costituenti più semplici, l’oggetto immerso nello spazio tridimensionale (per es., la superficie della piramide) è ridotto a una serie di figure piane.
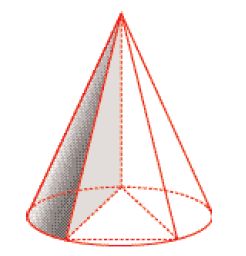
Si potrebbe tentare di misurare anche l’area della superficie del cono in base a questo principio, ma in questo caso la decomposizione non è più possibile (la superficie del cono non è composta da un numero finito di superfici più piccole, ma se mai di un numero infinito di rette). È possibile invece fare ricorso alla tecnica dello ‘schiacciamento’, che permette anch’essa la riduzione a oggetti più semplici. Se non abbiamo un’uguaglianza per la super - ficie del cono, abbiamo però due disuguaglianze tra oggetti più semplici; infatti la detta superficie è minore di ogni superficie piramidale circoscritta e maggiore di ogni superficie piramidale inscritta. Quanto valgano le aree delle superfici di queste piramidi lo sappiamo grazie alla decomposizione del passo precedente; la superficie del cono è così ‘schiacciata’ tra due superfici che differiscono soltanto per le basi, come nel caso di un cerchio compreso tra due poligoni regolari, l’uno circoscritto e l’altro inscritto (e dove per semplicità si possono scegliere poligoni con lo stesso numero di lati). Ora, Archimede aveva mostrato in precedenza come costruire due poligoni regolari simili, uno inscritto e l’altro circoscritto a un cerchio, in modo tale che il rapporto dei loro perimetri sia minore di ogni prefissato rapporto (prop. 3), e ciò permette la decomposizione finale, questa volta una decomposizione logica che trasforma lo schiacciamento in un argomento logico, inconfutabile quanto quello della decomposizione nel caso più semplice degli oggetti rettilinei.
Possiamo infatti decomporre uno spazio logico come si fa con uno spazio geometrico. Nel confrontare due superfici fra loro, dal punto di vista logico il problema può essere diviso nei tre casi seguenti: una superficie è più grande, uguale o più piccola dell’altra. In particolare, per la superficie laterale del cono vi sono soltanto tre possibilità: o è uguale a un triangolo che ha per base la circonferenza di base del cono e per altezza il lato del cono (che chiamiamo ‘triangolo di misura’), o è maggiore, o è minore. L’uguaglianza fra la superficie laterale del cono e quella del detto triangolo costituirebbe la generalizzazione del risultato precedente riguardante le piramidi. Ora, cominciamo a esplorare questo spazio logico, supponendo dapprima che la superficie sia maggiore di quella del detto triangolo. Essendo maggiore, lo sarà di un certo rapporto, r, e prendiamo allora poligoni inscritti e circoscritti il cui rapporto è minore di r : la superficie del cono (C) ha rispetto al triangolo di misura (T ) rapporto maggiore di quello che il poligono circoscritto ha rispetto a quello inscritto e, di conseguenza, maggiore del rapporto che la superficie laterale di una piramide circoscritta, PC , ha rispetto a quella di una piramide inscritta, PI , vale a dire C:T>PC:PI , da cui C:PC>T:PI. Si è già dimostrato che l’area della superficie del cono è minore di quella della superficie della piramide circoscritta, ossia C<PC, e si può dimostrare (tenendo presente che la lunghezza di una circonferenza è maggiore del perimetro di un poligono inscritto, come si desume dai postulati contenuti in questo trattato) che l’area T del triangolo di misura è maggiore di quella, PI, della piramide inscritta, ossia T>PI. Un momento di riflessione permette di vedere che le tre disuguaglianze appena scritte sono tra loro incompatibili. Con lo stesso procedimento si dimostra che l’area della superficie del cono non può essere minore di quella del triangolo di misura e dunque può essere soltanto uguale.
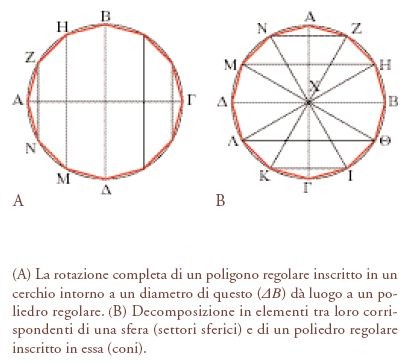
Questa è la struttura logica del primo tentativo serio di ottenere delle misure presentato da Archimede nelle proposizioni 13 e 14 del Libro I dell’opera Della sfera e del cilindro: decomposizioni di decomposizioni e riduzioni di riduzioni al servizio del passaggio dal curvo al rettilineo. Due sono le fasi principali: la prima è la decomposizione di un oggetto complesso in oggetti ‘atomici’ più semplici, mentre nella seconda coppie di oggetti complessi inscrivono e circoscrivono un oggetto ancora più complesso. Un’argomentazione basata sulla decomposizione dello spazio logico riduce così l’oggetto complesso a uno più semplice, facendo ricorso a trasformazioni di disuguaglianze fra rapporti. Nella prop. 13 Archimede si occupa del cilindro e il cono è ‘attaccato e vinto’ nella prop. 14, grazie a un’argomentazione ancora più complessa: è aggiunta un’ulteriore trasformazione del triangolo di misura che oscura in parte la relazione tra le dimostrazioni di queste due proposizioni e quelle delle precedenti. Infine, alla sfera è applicata un’analoga procedura nelle proposizioni 33- 34: essa è schiacciata tra due solidi di rotazione (figure ottenute per rotazione di poligoni nello spazio, fig. 4A)) che a loro volta sono decomposti in coni e altri solidi di tipo conico e nelle loro superfici (fig. 4B). La struttura logica portante di quest’opera consiste quindi in una riduzione che avviene in due fasi, da sfere a coni e da coni a piramidi, ciascuna fase basandosi a sua volta su un’operazione, anch’essa in due fasi, che fa intervenire decomposizioni spaziali, schiacciamento del solido tra altri due solidi e decomposizione logica.
L’aspetto più notevole di questa operazione è forse il fatto che la sfera stessa non è quasi mai menzionata direttamente: essa risulta come implicazione alla fine di un lungo ragionamento, come un’impalcatura che permette di inscrivere e circoscrivere solidi di rotazione, un oggetto menzionato solo di sfuggita nel corso di una riduzione all’assurdo. Ritroviamo la sfera, punto di partenza e di arrivo del ragionamento, perdendola di vista; ci muoviamo come sonnambuli verso di essa. Ma perdiamo anche di vista il vero punto di partenza di questo ragionamento, Archimede. L’impressione di muoversi come sonnambuli verso la sfera si sposa con l’impressione di trovarsi di fronte a un testo senza autore, non però nel senso di un testo caotico, senza uno sviluppo chiaramente percepibile, ma nel senso di uno sviluppo miracoloso che procede senza sforzo. Archimede riesce a fornire una misura logicamente ineccepibile senza che nulla del suo aspetto miracoloso vada perduto.
È utile fare un confronto con il Libro XII degli Elementi di Euclide, che tratta della misura di oggetti come il cono (seguendo probabilmente un trattato di Eudosso). Decomposizione e schiacciamento sono strumenti di cui si fa uso anche in questo libro e ciò significa che erano conosciuti prima di Archimede. Già Ippocrate conosceva la decomposizione (v. cap. XVI) ed Eudosso fu probabilmente l’inventore dello ‘schiacciamento’, o ‘esaustione’, come si dice talvolta (v. cap. XVII). Tuttavia, il Libro XII non è brillante come Della sfera e del cilindro, che è una vera e propria opera d’arte: mentre Archimede cammina come in sogno verso la sfera, Euclide maltratta il cono finché non riesce a misurarlo. Un altro aspetto dell’arte di Archimede, ancora più difficile da definire, riguarda l’eccezionale bellezza degli oggetti nei quali è decomposta la sfera. Il significato di Della sfera e del cilindro, sia dal punto di vista estetico sia da quello matematico, sta nel risultato ottenuto: la riduzione dimensionale della sfera.
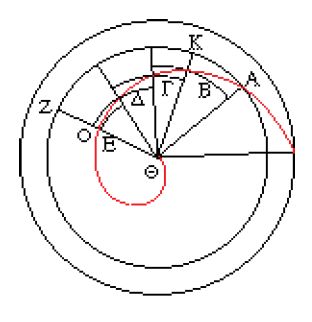
Le riduzioni dimensionali sono importanti sia come risultati in sé sia perché permettono di risolvere altri problemi. Sulla scia di alcuni risultati del Libro I, nel secondo e più avanzato libro dell’opera Della sfera e del cilindro Archimede enuncia e risolve un certo numero di problemi. Per esempio, così come la sfera intera è ridotta a un cono, anche i segmenti sferici si possono ridurre a coni. Nella prop. 2 si mostra come procedere (fig. 5): il cono B∆Z è equivalente al segmento sferico BΓZ, mentre il cono BZK è equivalente al segmento BAZ. La riduzione a coni è una riduzione di dimensione, perché sappiamo che i volumi dei coni con una data base sono proporzionali alle altezze: il rapporto tra i due coni, cioè il rapporto tra i due segmenti sferici, è uguale al rapporto tra i due segmenti rettilinei KE, EΔ. La riduzione di un rapporto curvilineo tridimensionale a uno rettilineo unidimensionale è una riduzione notevolissima, che consente la risoluzione di problemi che altrimenti sembrerebbero fuori portata. È il caso, per esempio, del problema di dividere la sfera secondo un dato rapporto: se si vuole prendere un terzo della sfera, dove va tagliata? Archimede è in grado di dare una risposta precisa a domande di questo genere, anche se per vie a volte tortuose. Per esempio, le rette KE ed EΔ sono funzione dei corrispondenti segmenti sferici, ma questa funzione è molto complicata e si esprime con relazioni che oggi chiamiamo equazioni cubiche: il Libro II è in gran parte dedicato a equivalenti geometrici delle equazioni cubiche. Benché l’espressione ‘equazioni cubiche’ non corrisponda alla realtà dell’epoca, essa ha un significato storico perché nel Medioevo, per esempio nell’Algebra di ‛Umar Ḫayyām, lo studio del trattato di Archimede fu il punto di partenza per lo studio algebrico delle equazioni, sia quadratiche che cubiche.
Gli studi sulla sfera da parte di Archimede ebbero quindi successo, furono letti e apprezzati, furono citati e utilizzati da vari autori, come Erone e Pappo, mentre i problemi da lui sollevati portarono a ulteriori ricerche. Tuttavia, si è trattato di un successo a spese dell’Archimede storico: le opere sulla sfera e il cilindro che possediamo non sono quelle che Archimede scrisse di proprio pugno. Tutto fa pensare infatti che egli scrivesse nel proprio dialetto, il dorico, mentre la tradizione manoscritta è nel dialetto greco postclassico, la koinḗ. È difficile dire come e quando Archimede sia stato tradotto; è possibile che la trascrizione nella koinḗ abbia comportato solamente qualche banale cambiamento fonetico, del tipo ‘η’ della koinḗ al posto della ‘α lunga’ del dorico, ma è anche possibile che vi siano stati interventi sul contenuto matematico. La figura di Archimede è perciò più misteriosa di quanto egli avrebbe voluto; per quanto riguarda ciò che gli antichi consideravano la sua migliore riuscita, il cerchio, Archimede ancora di più fu vittima del successo, poiché il trattato sulla Misura del cerchio, che porta il suo nome, è anch’esso scritto nella koinḗ e non in dorico, ed è probabilmente soltanto un’opera tarda basata su fonti archimedee. Probabilmente l’interesse per l’opera fu tale che gli autori posteriori non soltanto la tradussero, ma la trasformarono in qualcosa che secondo loro era più leggibile.
Secondo l’ipotesi più accreditata, dovuta a W.R. Knorr, quest’opera ci è pervenuta in una redazione molto tarda dovuta a Ipazia, filosofa e matematica alessandrina del V sec. d.C. (più di 400 pagine di Knorr 1989 sono dedicate allo studio della storia del testo di questo trattato). Di conseguenza, le argomentazioni che ci sono pervenute non sarebbero dovute ad Archimede; tuttavia, molto probabilmente si devono a lui i risultati, che possono essere paragonati a quelli che riguardano la sfera. Archimede dimostra per prima cosa un’uguaglianza tra il cerchio e un altro oggetto più semplice: nel caso della sfera, questa aveva un rapporto semplice con un cono, mentre nel caso del cerchio si ha l’uguaglianza con un triangolo. Non si tratta proprio della quadratura del cerchio, perché il triangolo in questione non si può definire indipendentemente dal cerchio; si tratta infatti di un triangolo rettangolo, un lato del quale è uguale al raggio mentre un altro, e questo è più problematico, è uguale alla circonferenza. L’intuizione è simile, la sfera si può pensare come uno strano cono ripiegato su sé stesso, che ha per base la superficie della sfera e per altezza il raggio e, analogamente, il cerchio può essere visto come uno strano triangolo ripiegato su sé stesso che ha per base la circonferenza e per altezza, anche in questo caso, il raggio. Se nel caso della sfera, però, si ha la riduzione a un oggetto geometrico indipendente (la superficie risulta infatti equivalente a quattro volte quella del cerchio massimo), un’uguaglianza altrettanto semplice non esiste per la circonferenza del cerchio. In assenza di questa uguaglianza, Archimede maggiora e minora la lunghezza della circonferenza, dimostrando che il rapporto di questa con il diametro non può superare un certo rapporto né essere inferiore a un altro. Si tratta anche qui di ‘schiacciare’, anche se questa volta lo schiacciamento non ha lo scopo di eliminare i casi di di - suguaglianza finché non si raggiunge l’uguaglianza, ma soltanto di restringere gli estremi superiore e inferiore (si confronti questo procedimento con quello di Aristarco per misurare la grandezza e la distanza del Sole e della Luna: v. cap. XXI). Per ottenere lo schiacciamento limite si costruiscono poligoni con molti lati, del tipo di quelli utilizzati nell’opera Della sfera e del cilindro, e se ne misura il perimetro. Il risultato, ottenuto arrivando a un poligono con 96 lati, è che la circonferenza del cerchio è compresa tra 3+(1/7) e 3+(10/71) volte il diametro. Questo risultato è molto più di un banale calcolo, e in particolare presuppone un’approssimazione della radice quadrata di 3: determinare un valore approssimato di π (il rapporto fra la circonferenza e il diametro) richiede dunque altre approssimazioni. Può darsi che nell’opera originale di Archimede fosse chiarito come ottenere queste ultime, ma non possiamo saperlo con certezza, ed è possibile soltanto fare congetture al riguardo, basate unicamente sui numeri stessi.
La matematica meccanica
In alcuni trattati di Archimede gli oggetti presi in esame si possono considerare sia oggetti fisici sia oggetti matematici considerati come fisici, e questo è forse il problema maggiore che presenta l’opera di Archimede. Cercheremo di offrire una possibile soluzione di tale questione, con l’avvertenza che si tratta di una questione controversa e difficile.
I trattati in questione si dividono in due gruppi (conservati almeno in parte in dialetto dorico, e dunque probabilmente abbastanza vicini all’originale). Il primo gruppo comprende quattro trattati di meccanica: due sui centri di gravità (i due libri dell’opera Sull’equilibrio dei piani) e due sui corpi nei liquidi (i due libri dell’opera Sui corpi galleggianti); il secondo gruppo include due trattati nei quali la meccanica è applicata alla matematica (La quadratura della parabola e il Metodo). I due gruppi di trattati sollevano ciascuno un problema. Per quanto riguarda il primo, ci si può chiedere come possa un’analisi di carattere puramente teorico e matematico dimostrare qualcosa intorno al mondo fisico. Perché mai la matematica dovrebbe vincolare il mondo? Per il secondo, il problema è se una considerazione di carattere empirico possa dimostrare un risultato puramente matematico. Il primo problema ha un significato filosofico molto più ampio; tuttavia, almeno per quanto concerne Archimede, una risposta al secondo problema è rilevante anche per il primo. Per illustrare la situazione, ben si presta un esempio che riguarda un problema del primo tipo: la dimostrazione di Archimede della ‘legge della leva’, cui è dedicata la Tav. I. Poiché, ovviamente, la legge della leva non fa parte delle ipotesi preliminari alla prop. 6 dalla quale si parte nella dimostrazione citata, abbiamo un aumento di informazione come risultato di un’argomentazione matematica, e i risultati della matematica dicono di più degli assiomi; infatti non è immediato che il teorema di Pitagora sia già contenuto negli assiomi di Euclide. In questo senso la matematica produce informazioni, perché porta alla luce più di quanto non dicano le ipotesi. Questo potrebbe essere anche il caso della fisica matematica di Archimede; l’informazione che riceviamo sul mondo fisico è però solo condizionale: non possiamo semplicemente dire che vale la legge della leva, bensì che essa è valida se si verificano certe ipotesi. Il problema dell’applicabilità della matematica alla fisica è, quindi, in parte riducibile a quello dell’informazione fornita da un’argomentazione matematica e in parte si risolve rilevando la natura condizionale della conoscenza fisico-matematica.
Senza provare a rimuovere subito le perplessità che il problema della leva e, in generale, i problemi del primo tipo, fanno nascere sul rapporto tra matematica e mondo fisico, passiamo ora al secondo problema, l’applicazione della meccanica alla matematica. Ci riferiremo a un esempio tratto dalla prima proposizione del Metodo sui teoremi meccanici a Eratostene (Tav. II), per cercare infine una risposta alle questioni che i due gruppi di problemi fanno nascere insieme.
Qui siamo di fronte a ricerche matematiche ancora più avanzate, come in genere sono quelle contenute nel Metodo. Si tratta di un’opera difficile, in molti sensi, e per di più con una storia romanzesca; menzionata da autori antichi come di Erone, data per perduta in età moderna, fu scoperta in un palinsesto a Istanbul (contenente molte altre opere di Archimede che conosciamo da altre fonti e che spesso integra). Il manoscritto, pubblicato a cura di I.L. Heiberg, è un antico testo bizantino coperto da scritti religiosi più tardi; alla fine della Prima guerra mondiale scomparve, lasciando dietro di sé una ridda di voci, per ricomparire poi a un’asta da Christie’s, a New York, il 29 ottobre 1998, dove fu venduto per oltre due milioni di dollari; li vale tutti, perché è l’unica testimonianza di uno dei momenti più alti della storia della matematica.
La prima proposizione di questo trattato costituisce un esempio relativamente semplice dell’applicazione del metodo meccanico di Archimede. Il problema considerato è quello di misurare un segmento parabolico, dunque un oggetto curvilineo. Archimede aveva qualche perplessità a proposito di questo bellissimo risultato; certo, ne era sufficientemente orgoglioso per diffonderlo, ma non senza aggiungere qualche riserva. Il Metodo, che è in forma di lettera a Eratostene, è molto più dialogico della maggior parte delle opere greche di matematica. Nell’introduzione alle dimostrazioni Archimede afferma:
Decisi di scriverti e di esporti nello stesso libro le caratteristiche di un certo metodo, mediante il quale ti sarà data la possibilità di considerare questioni matematiche per mezzo della meccanica. E sono persuaso che questo [metodo] sia non meno utile anche per la dimostrazione degli stessi teoremi. E infatti alcune delle [proprietà] che a me dapprima si sono presentate per via meccanica sono state più tardi [da me] dimostrate per via geometrica, poiché la ricerca [compiuta] per mezzo di questo metodo non è una [vera] dimostrazione.
Dopo la prop. 1, Archimede s’interrompe, un atteggiamento molto poco comune nella matematica greca, per fare la seguente considerazione: «Ciò dunque non è stato [veramente] dimostrato per mezzo di quel che è stato detto; ma è stata fornita un’indicazione che [induce a ritenere che] la conclusione sia vera: perciò noi, vedendo che la conclusione non è stata dimostrata, ma presumendo che essa sia vera, proporremo la dimostrazione per via geometrica da noi stessi trovata, che avevamo già prima pubblicata». Il riferimento è alla Quadratura della parabola, dove egli dimostra mediante decomposizioni (finite) e schiacciamenti ciò che qui dimostra mediante decomposizioni (infinite) ed equilibri.
Che la dimostrazione di un fatto geometrico mediante considerazioni relative alla meccanica facesse sorgere problemi era dunque un fatto sentito anche da Archimede. Da un punto di vista filosofico è forse possibile considerare l’applicazione della matematica alla fisica come una sorta di vincolo: quali che siano le proprietà dell’Universo fisico, esso ha anche proprietà matematiche, e queste lo vincolano nel senso che se esso gode di una certa proprietà allora gode necessariamente anche delle proprietà espresse dai corollari matematici di quella. Il vincolo imposto è dovuto alla natura astratta e generale della matematica. Se ciò può spiegare l’applicabilità della matematica alla fisica, ha senso però invertire l’ordine e ammettere che il comportamento di una leva possa influenzare la natura di una retta, di un triangolo o di una parabola? Si può certo immaginare un diverso sistema di gravità nel quale la legge della leva non vale più. Che cosa succede allora alla parabola? In altre parole, la prop. 1 del Metodo vale ancora in altri spazi?
Archimede non nasconde il suo disagio nell’applicazione della meccanica alla matematica, ma, anche registrando questo disagio non dobbiamo perdere di vista alcune circostanze importanti. Per prima cosa, egli continuò questa linea di ricerca; inoltre, la dimostrazione della prop. 1 contenuta nel Metodo è corretta, come pure le altre di questo trattato: per qualche ragione che dobbiamo cercare di capire, il Metodo è dopo tutto valido dal punto di vista geometrico; infine va sottolineato che se la prop. 1 presenta problemi di natura logica, questi non sono dovuti soltanto alla meccanica. Anzi, solleva più problemi la decomposizione infinita: che cosa significa infatti dire che un triangolo o un segmento parabolico è la ‘somma delle proprie rette’? Tutti questi fattori rendono più difficile considerare il Metodo come un approccio euristico basato sulla meccanica; si tratta non meno di un approccio di tipo dimostrativo e il metodo della decomposizione infinita è in un certo senso precursore del calcolo integrale (come è di solito riconosciuto nella storia dell’analisi matematica).
Per Archimede, però, l’essere precursore di qualcosa non poteva essere motivo di conforto; per quanto lo riguardava, egli utilizzava una tecnica molto ambigua, quello che oggi chiameremmo ‘il metodo degli indivisibili’. Questo problema si può forse chiarire se si considera il Metodo come un gioco, una sorta di gioco a nascondersi inventato da Archimede. Come nella sua opera Della sfera e del cilindro la sfera salta fuori a sorpresa in mezzo a oggetti apparentemente irrilevanti, così nel Metodo il segmento parabolico, come pure altri oggetti geometrici, compare a sorpresa tra leve e rette. Il fatto che sia difficile per noi seguire il filo logico del Metodo è sicuramente intenzionale da parte di Archimede; torneremo in seguito su questo punto. Il gioco e la sorpresa non sono però il punto essenziale della sua opera. Ciò che è veramente notevole nel Metodo non è l’abilità ma il valore matematico, una singolare validità matematica. Torniamo infatti al modo in cui Archimede dimostra la legge della leva (Tav. I); questa legge segue da alcune ipotesi, e, qui sta il punto cruciale, non si tratta di ipotesi di carattere fisico. Archimede non coglie qualche comportamento particolare della gravità, dalla quale l’analisi fatta è assolutamente indipendente. Le ipotesi si basano tutte su una riconcettualizzazione di oggetti fisici come oggetti puramente geometrici; Piani in equilibrio è un’opera puramente geometrica e non si basa su esperimenti né ha bisogno di essi. Egli non utilizza principî geometrici per lo studio dell’equilibrio, ma, al contrario, ridefinisce i concetti di ‘equilibrio’ e di ‘centro di gravità’ in termini puramente geometrici e di teoria delle proporzioni, che diventano così concetti propri della geometria e della teoria delle proporzioni, quali utili abbreviazioni di complesse manipolazioni matematiche.
Alla luce di tutto questo – e non sappiamo se e quanto Archimede ne fosse cosciente – possiamo riconsiderare i due problemi dell’applicazione della matematica alla meccanica e della meccanica alla matematica, e concludere che Archimede non fa né una cosa né l’altra. Egli si limita a dimostrare che certe ipotesi geometriche implicano certe conseguenze, restando sempre, per quanto lo riguarda, all’interno della matematica. È questa la logica che sottende il progetto archimedeo.
Il significato storico di questa analisi logica è meno chiaro. È evidente che la sua ‘meccanica’, almeno per quanto riguarda i trattati in questione, non implica ‘osservazioni’ o ‘esperimenti’, che sarebbero stati fuori luogo (viene in mente il modo in cui Gauss cercava di calcolare la somma degli angoli di triangoli fisici, ma questo era in un contesto posteuclideo). Quanto poi la sua mente precorresse la logica servendosi dell’intuizione che gli fornivano la leva e la gravità (o, nel caso dei Corpi galleggianti, i corpi immersi nell’acqua) è un’altra storia. È probabile che pensasse in modo semintuitivo, e che dietro il disagio di cui parla nel Metodo si nascondesse la coscienza di questo fatto.
Nuovi oggetti
Con l’invenzione di nuovi oggetti Archimede supera un’altra frontiera. Crea oggetti insoliti, ma stranamente familiari, che sembrano sfidare ogni possibilità di misura; poi, colpo di scena, ecco la misura. È quanto egli fa in Conoidi e sferoidi e in Spirali, opere tra le più avanzate del corpus archimedeo, in quanto sono richiesti lemmi molto complicati per dimostrarne i risultati principali. Conoidi e sferoidi provengono da sezioni coniche e sono perciò paragonabili, per ciò che riguarda la misura, a quanto abbiamo già visto a proposito del segmento parabolico nel Metodo e nella Quadratura della parabola. Si tratta di un modo di procedere molto comune nella storia della matematica, ciò che era stato introdotto come possibile soluzione (le sezioni coniche per risolvere il problema della duplicazione del cubo: v. cap. XVII) è riproposto come problema. Il segmento parabolico è un esempio di oggetto bidimensionale che nasce da sezioni coniche; i conoidi e gli sferoidi ne sono l’equivalente tridimensionale. Se si prende un’ellisse e la si fa ruotare intorno a uno dei suoi assi, si ottiene un solido a forma di uovo, simmetrico, che Archimede chiamò ‘sferoide’ (fig. 7A), interessandosi in particolare ai segmenti che si ottengono segando lo con piani ortogonali all’asse di rotazione oppure obliqui rispetto a esso; prendendo invece un segmento parabolico e facendolo analogamente ruotare intorno all’asse, il risultato è un oggetto simile a un cono, e detto perciò ‘conoide’ (fig. 7B); un analogo conoide, ma più ‘aperto’, si ottiene facendo ruotare un segmento iperbolico.
Questi oggetti sono molto lontani dal l’esperienza quotidiana: occorre prendere un cono, secarlo con un piano, ruotare la figura ottenuta e continuare secando questa con altri piani. Sembra improbabile che oggetti di questo tipo si prestino a una misura semplice, di qui la sorpresa. Archimede dimostra che i segmenti di conoide o di sferoide sono uguali a un cono che ha per base la base del segmento e per altezza una funzione delle date sezioni coniche. Con lo stesso procedimento si riduce la misura del volume della sfera a quella del volume del cono; in altri termini, si riducono oggetti ottenuti ruotando linee curve (un cerchio nel caso della sfera, sezioni coniche per conoidi e sferoidi) a oggetti ottenuti ruotando una linea retta (il caso del cono). Il mondo viene così reso meno curvo.
Decomposizione e schiacciamento sono le tecniche usate in tutta l’opera. Qui la decomposizione è più diretta (gli oggetti rilevanti sono immaginati con tronchi di cilindro all’interno e all’esterno, come monete l’una sopra l’altra: fig. 8). Il trattato è forse meno elegante di altri ed è relativamente complesso; esso si basa su proposizioni della teoria delle sezioni coniche molto più specifiche di quelle usate in altre opere e anche su risultati di carattere particolare come il seguente, enunciato senza dimostrazione nell’introduzione:
Se sono date quante si vogliano grandezze ciascuna delle quali superi l’altra [la precedente] di una uguale [differenza], e se altre grandezze sono in ugual numero di quelle, e ciascuna grandezza di esse è uguale alla maggiore [di quelle], [la somma di] tutte le grandezze ciascuna delle quali è uguale alla maggiore [tra quelle], sarà minore del doppio [della somma di] tutte le grandezze che si superano di una uguale differenza, e maggiore del doppio [della somma] di tutte le grandezze restanti, eccettuata la massima.
Come si vede nella fig. 8, questo risultato sarà applicato quando si dovrà considerare la serie dei raggi dei cerchi secati dalla curva; naturalmente, l’insieme delle due disuguaglianze è utile per il metodo dello schiacciamento. Archimede sostiene che la dimostrazione di questa proposizione «è manifesta». Si tratta di un risultato che riguarda la somma di una serie aritmetica ed è interessante vedere come egli si trovi a proprio agio nel riferirsi a questo argomento (le serie erano in generale di scarso interesse nella matematica greca, più propensa alla visione geometrica) e con quale facilità affermi che il risultato è ovvio. Se è difficile dire se il risultato fosse ovvio per i suoi lettori, non era però certamente ovvia la sua utilità per misurare conoidi e sferoidi; ciò è un altro esempio del giocare a nascondersi tipico di Archimede.
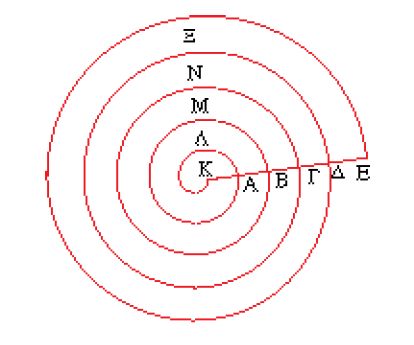
Se conoidi e sferoidi sono il risultato di un solo movimento – una rotazione di piani che genera solidi –, le spirali, curve inventate con tutta probabilità da Archimede stesso, sono il risultato di due movimenti, uno rotatorio e uno lineare, che generano una curva complicata. Poiché i due movimenti devono essere in una data relazione, in questo caso il tempo è un fattore che entra in gioco. Non è così nel caso dello sferoide: si può generare lo sferoide cominciando col ruotare un’ellisse, diciamo di un terzo di una rotazione completa, per poi lasciarla da parte e ritornare a essa in seguito per ruotarla ancora un po’, finché una rotazione completa non costruisce il solido. Il tempo e il passo sono del tutto arbitrari, perciò in un certo senso non c’è alcun movimento propriamente detto, e il tempo non ha importanza. Per la spirale le cose stanno diversamente. Nell’introduzione al trattato Spirali, essa è definita come segue (fig. 9): «se una linea retta [KE], rimanendo [fermo] un estremo, è fatta rotare nel piano con velocità costante fino a farla tornare di nuovo nella posizione dalla quale è partita, e insieme con la retta rotante si muove un punto sulla retta con velocità costante cominciando dall’estremo fisso [K], il punto descrive nel piano una spirale [KABΓ∆…, con i rami ΛMNΞ...].».
La curva può dunque essere costruita soltanto se i due movimenti hanno luogo a velocità costante; ogni perturbazione, che si traduce in un rallentamento relativo di uno dei due moti, porta a una deformazione della curva. Il tempo entra pertanto in modo essenziale nella definizione. Non sappiamo se Archimede fosse consapevole di tutto ciò; da quanto abbiamo visto a proposito dei suoi interessi matematici sembra che egli attribuisse importanza non tanto alla legittimità degli oggetti, bensì al fatto che, per quanto fossero complicati, potevano sempre essere misurati. Da questo punto di vista la natura complicata della spirale non era dissuasiva ma, al contrario, lo spronava.
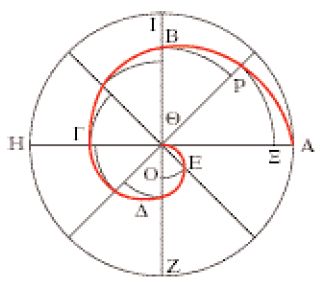
Archimede riesce a ridurre la spirale a cerchi, ossia riduce un oggetto curvilineo che richiede un movimento a un altro, anch’esso curvilineo, ma questa volta statico. Consideriamo l’area spazzata da una rotazione completa della spirale (fig. 11), vale a dire fermiamo il movimento della spirale quando la componente circolare ha compiuto un giro completo, e uniamo il punto d’arrivo A con quello di partenza Θ, racchiudendo così una figura piana: nella prop. 24 si dimostra che questa area è uguale a un terzo del cerchio, di raggio ΘA, che racchiude la spirale. Come nel caso della sfera, si ottiene in questo modo non soltanto una semplificazione, ma oltretutto una semplificazione che comporta un rapporto numerico semplice. Questo però è soltanto il primo giro. La spirale continua, e ogni giro spazza una nuova area (tralasciamo ogni volta le aree dei giri precedenti). Il secondo giro spazza 7/12 del secondo cerchio che è attraversato (prop. 25). Infine, nella prop. 27 si considerano tutte le rotazioni: delle aree delle figure comprese dalle spirali e dalle rette in rotazione, la terza è doppia della seconda, la quarta tripla (sempre della seconda), la quinta quadrupla e così via, tutti rapporti numerici semplici (si ha infatti una progressione aritmetica).
In qual modo Archimede arriva al risultato? La tecnica ormai la conosciamo: la figura della spirale è riconcettualizzata pensandola composta da settori consecutivi, i quali sono poi ‘schiacciati’ tra settori circolari maggiori e minori di questi (fig. 12). Esaminando i risultati che permettono di sviluppare questa idea, ci rendiamo conto che nemmeno l’organizzazione del trattato è nuova, con il suo modo sottile di predisporre la misura, per così dire accerchiandola. Una prima parte comprende due risultati sul moto uniforme, una seconda sette proposizioni che risolvono vari problemi sul cerchio e che sembrano non avere relazione con la spirale. Per esempio, nella prop. 5, dato un cerchio e una retta tangente a esso, si mostra come trovare un segmento di retta KZ tale che il rapporto ZΘ:ΘK, con Θ punto di tangenza, sia piccolo a piacere (risultati di questo tipo saranno utili nelle dimostrazioni che si basano sullo schiacciamento di settori circolari). Ancor di più la terza parte, costituita dalle propp. 10 e 11, è completamente al di fuori di qualunque cosa che somigli a una spirale. Archimede introduce alcuni teoremi ‘astratti’ sulle progressioni, come in Conoidi e sferoidi, ma di natura più complessa. Come ha dimostrato E.J. Dijksterhuis, la prop. 10 è equivalente, usando il simbolismo algebrico moderno, alla formula: 12+22+…+n2=(1/6)n(n+1)(2n+1). Vale la pena confrontare con la complicata formulazione originale:
Se sono date quante si vogliano linee, una dopo l’altra, tali che ciascuna di esse superi la seguente di una uguale quantità, e tali che l’eccesso [dell’una rispetto all’altra] sia uguale alla minore delle linee; e se sono date altrettante linee ciascuna delle quali sia uguale in grandezza alla maggiore [delle linee prima date], i quadrati delle linee uguali alla maggiore, [sommati] con il quadrato della maggiore e [sommati] con il rettangolo della minore e [della somma] delle linee che si superano [l’una rispetto all’altra], saranno il triplo [della somma] di tutti i quadrati delle linee che si superano. (Spirali, prop. 10)
Anche se Archimede traduce questo enunciato in una figura con lettere, le operazioni che portano alla dimostrazione comportano espressioni complicate del tipo di quelle dell’enunciato, per cui questa proposizione assomiglia poco a quelle dell’algebra del liceo, al contrario della precedente formula equivalente data da Dijksterhuis, ed è invece più vicina alla logica matematica moderna: astratta, complicata e rigorosa. Ciononostante, non è opportuno concludere che Archimede mancasse del moderno simbolismo algebrico, anche se ciò è a rigore vero; in effetti, non siamo in presenza di una mancanza, ma di un successo, un’operazione di grande effetto e funzionale proprio per la sua oscurità, che rende difficile immaginare come egli sia potuto entrare nello studio della spirale.
Nel seguito del trattato, da una progressione di settori circolari si ottiene una successione di quadrati in progressione aritmetica; di qui l’importanza di questi risultati per la decomposizione che Archimede adotterà. Questa è la terza parte, la più singolare delle Spirali; egli introduce poi i concetti principali, segnalando in questo modo l’inizio dello studio delle spirali vere e proprie. Nella quarta parte (propp. 12-23) si stabiliscono alcuni risultati sulle spirali che saranno usati nell’ultima parte (propp. 24-25) per ottenere le misure. Per l’inventiva di cui dà mostra Archimede, per i risultati che egli presenta, brillanti nella loro semplicità, e per l’organizzazione particolarmente felice da lui ideata, Spirali si può considerare la sua opera migliore.
Il gioco archimedeo
Un’analisi di alcune opere di carattere più eccentrico, può essere illuminante per capire la natura della scienza di Archimede. Immaginiamo di essere seduti nel nostro studio ad Alessandria quando arriva un messo dal porto il quale ci consegna, con nostro grande piacere, un nuovo rotolo di papiro di Archimede arrivato da Siracusa. Non vediamo l’ora di sapere cosa contenga. La misurazione di qualche altro oggetto, o un nuovo oggetto inventato e misurato? Chissà, finalmente la quadratura del cerchio! Cominciamo a leggere con impazienza, ma ci accorgiamo del fatto che qualcosa non va: «Amico, se partecipi della sapienza calcola, usando diligenza, qual era il numero dei buoi del Sole che pascolavano […]. In ciascun gruppo c’erano tori in quantità, divisi secondo la seguente proporzione: immagina, o amico, che i [tori] bianchi fossero in numero uguale a una metà più un terzo dei neri, più tutti i fulvi» (Il problema dei buoi).
Intanto, questo problema è proposto in versi (Archimede era anche poeta). L’epigramma continua con un complicato elenco di affermazioni su otto ‘incognite’ (quattro mandrie, ciascuna divisa in un numero non precisato di tori e di vacche). Oggi potremmo dire che sette delle affermazioni sono equazioni, due delle quali del genere che si ritrova nella moderna teoria dei numeri: una certa somma è un ‘numero rettangolare’, cioè della forma pxq, un’altra è un ‘numero triangolare’, cioè della forma px(p+1)/2. Cosa fare con questi dati? Apparentemente occorre calcolare la somma delle otto incognite ma, riflettendoci, perché farlo? Solo perché Archimede lo ha chiesto?
Non sappiamo se qualcuno ad Alessandria abbia mai provato a risolvere questo problema. Carl Amthor lo fece, nel 1880, e, anche se non trovò la soluzione completa, fu in grado di dimostrare, con l’ausilio di tecniche matematiche moderne, che la soluzione più semplice aveva 206.545 cifre (nella nostra notazione decimale). In altri termini, i buoi del Sole sono moltissimi, una quantità quasi impossibile da esprimere con il sistema di numerazione dei Greci (cosa che solleva il problema dei limiti di questo sistema, sul quale torneremo tra un momento a proposito dell’Arenario). Tornando allo studio ad Alessandria, forse bisognerebbe pensare che Archimede volesse prenderci in giro, cosa che invece Amthor non capì.
In realtà il problema, anche se si esprime in termini semplici, non ha soluzione. Certo, Archimede non aveva ‘una soluzione’, qualunque cosa ciò significhi; tuttavia, era proprio una soluzione quel che l’epigramma chiedeva: chi riceveva il papiro doveva ammettere la sconfitta, oppure perdere tempo su un problema insolubile. Si tratta quindi di un gioco che, anche se usa la matematica, non è in realtà di matematica; non si tratta di manipolare numeri, ma di manipolare i lettori. Giochi poco rassicuranti. Ce ne sono altri che sembrano più innocenti, anche se ne sappiamo poco.
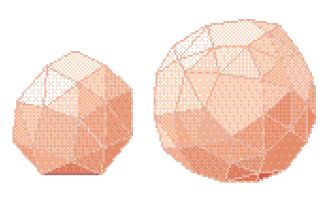
Lo Stomachion è un’opera strana; ce ne restano due frammenti, uno in greco e l’altro in arabo. Ha per oggetto un quadrato, suddiviso in un modo che ricorda ricreazioni geometriche più tarde (fig. 13). Che cosa richiedesse non sappiamo, ma sembra si dovesse dimostrare qualcosa (che un certo angolo è acuto, che certe figure sono commensurabili). Anche se sembra un gioco, Archimede lo sviluppò per fare osservazioni di genuino carattere matematico. Tutto ciò può essere messo a confronto con i poliedri ‘semiregolari’ da lui inventati. Dal Libro XIII degli Elementi di Euclide sappiamo che vi sono soltanto cinque solidi regolari, ma ve ne sono molti di più semiregolari, cioè tali che le facce sono ancora poligoni regolari ma diversi tra loro (due esempi, piuttosto semplici, sono illustrati nella fig. 14; Archimede ne costruì almeno tredici). Non sappiamo quale scopo avesse questa ricerca; tutto quello che abbiamo in proposito è una citazione nel Libro V di Pappo (v. cap. XIX). Vi si colgono aspetti archimedei ben noti: il piacere dell’invenzione geometrica, il notevole fascino dell’immagine visiva, un’invenzione che spalanca campi apparentemente caotici nei quali portare ordine. Quale fosse questo ordine non lo sappiamo; la sola cosa chiara è l’aria giocosa e vivace che si respira.
Aria giocosa la si ritrova anche nell’Arenario, l’opera che tra tutte quelle a noi pervenute è la più diversa per stile e contenuto. Una volta tanto non è indirizzata a uno studioso, bensì al re di Siracusa, Gelone. Il problema è di calcolare il numero di granelli di sabbia contenuti nell’Universo; da questo seguono altri due problemi: dare una stima della grandezza dell’Universo e trovare un sistema di numerazione capace di esprimere numeri estremamente grandi. Entrambi i problemi si affrontano facilmente. All’interno di un Universo che si suppone sferico, Archimede fa uso dell’ipotesi eliocentrica (questa è dunque la fonte migliore per il modello eliocentrico di Aristarco: v. cap. XXI), perché in tal modo l’Universo risulta più grande. Egli suppone quindi che l’orbita della Terra abbia con la grandezza dell’Universo lo stesso rapporto che nel modello geocentrico il diametro della Terra ha con l’orbita del Sole, e deve pertanto calcolare la distanza del Sole in termini della grandezza della Terra nel modello geocentrico. Archimede lo fa utilizzando osservazioni da lui stesso condotte e, naturalmente, estrapolazioni geometriche dalle misure ottenute. Ha così a disposizione stime per la grandezza assoluta della Terra, e quindi dell’orbita assoluta del Sole nel modello geocentrico, e di conseguenza anche della grandezza assoluta dell’Universo nel modello eliocentrico. Se ora immaginiamo quest’ultimo pieno solo di granelli di sabbia, e diamo un valore piccolissimo alla grandezza di uno di questo granelli, avremo un’idea del genere di numero che stiamo cercando; un numero che non si può esprimere nel sistema di numerazione greco. Archimede deve quindi inventare nuovi numeri. Consideriamo dapprima i vecchi numeri; essi arrivavano fino a 10.000x10.000, cioè a una ‘miriade di miriadi’, e andavano perciò da 1 a 108 (v. cap. XXIX, Tav. I). Questi (escluso l’ultimo) sono i ‘primi numeri’. Si prende allora come unità la miriade di miriadi, e si considerano ‘secondi numeri’; quelli compresi tra 108 e 108x108=1016; un secondo numero è dunque 108 volte un primo numero (per es., il ‘secondo numero’ 7 è 7x108); così, i ‘numeri terzi’ hanno come unità 1016, e via di seguito. Possiamo arrivare fino a numeri il cui numero d’ordine è una miriade di miriadi, e questo si può considerare come unità del ‘secondo periodo’, chiamando numeri del ‘primo periodo’ quelli finora considerati. Il procedimento si può poi estendere, cosa che Archimede fa anche se ha già a disposizione numeri a sufficienza per contare i granelli di sabbia (il calcolo è effettivamente svolto alla fine del trattato, dopo un lemma sulla determinazione di questi numeri).
Il sistema di numeri di Archimede termina però col periodo che ha il numero d’ordine miriade di miriadi, e ciò è rilevante. In altri termini, anche se questo sistema talvolta è presentato come se fosse equivalente a quello posizionale, Archimede non inventò nulla del genere. Senza dubbio egli aveva capito che in linea di principio si potevano inventare nuovi termini per nuovi metaordini e periodi, ma il suo sistema è finito; l’aggiunta di nuovi numeri dipende dall’aggiunta di nuovi nomi, e ciò è equivalente a quanto succedeva nel sistema greco normale (si potevano sempre inventare nuovi nomi per nuovi numeri). Archimede non ha dunque introdotto un sistema di numerazione ricorsivo con la fantasiosa scusa della misurazione del numero dei granelli di sabbia; al contrario, il suo sistema è impraticabile, l’ultimo esercizio scherzoso, coerente ma senza un serio significato, all’interno del gioco, coerente ma altamente non pratico, di misurare la quantità di sabbia nell’Universo. Quanto è caratteristico tutto ciò della sua opera? Non lo sappiamo, ma crediamo di non essere lontani dal vero dicendo che l’impegno di Archimede non si limitava al contenuto matematico delle dimostrazioni nel tentativo di convincere, ma includeva una ‘poetica’ della suspense e della sorpresa, nel tentativo di colpire i lettori e di disorientarli.
Bibliografia
Berggren 1976: Berggren, John L., Spurious theorems in Archimedes’ Equilibria of planes, book I, “Archive for history of exact sciences”, 16, 1976, pp. 87-103.
Dijksterhuis 1938: Dijksterhuis, Eduard Jan, Archimedes, Groningen, P. Noordhoff, 1938 (trad. it.: Archimede, con un saggio bibliografico di Wilbur R. Knorr, Firenze, Ponte alle Grazie, 1989).
Knorr 1976: Knorr, Wilbur R., Archimedes and the measurement of the circle: a new interpretation, “Archive for history of exact science”, 15, 1976, pp. 115-140.
– 1978a: Knorr, Wilbur R., Archimedes and the pre-Euclidean proportion theory, “Archives internationales d’histoire des sciences”, 28, 1978, pp. 183-244.
– 1978b: Knorr, Wilbur R., Archimedes and the spirals: the heuristic background, “Historia mathematica”, 5, 1978, pp. 43-75.
– 1978c: Knorr, Wilbur R., Archimedes’ Neusis-constructions in spiral lines, “Centaurus”, 22, 1978, pp. 77-98.
– 1985: Knorr, Wilbur R., Archimedes and the pseudo-euclidean catoptrics. Early stages in the ancient geometric theory of mirrors, “Archives internationales d’histoire des sciences”, 35, 1985, pp. 27-105.
– 1986a: Knorr, Wilbur R, Archimedes’ dimension of the circle: a view of the genesis of the extant text, “Archive for history of exact sciences”, 35, 1986, pp. 281-324.
– 1986b: Knorr, Wilbur R., On two archimedean rules for the circle and the sphere, “Bollettino di storia delle scienze matematiche”, 6, 1986, pp. 145-158.
– 1989: Knorr, Wilbur R., Textual studies in ancient and medieval geometry, Boston, Birkhäuser, 1989.
Mach 1915: Mach, Ernst, Die Mechanik in ihrer Entwickelung historischkritisch dargestellt, Leipzig, F.A. Brockhaus, 1901 (trad. it.: La meccanica nel suo sviluppo storico-critico, Torino, Boringhieri 1977).
Netz 1999: Netz, Reviel, Archimedes Transformed: the Case of a Result Stating a Maximum for a Cubic Equation, “Archive for history of exact sciences”, 1999.
Schneider 1979: Schneider, Ivo, Archimedes: Ingenieur, Naturwissen schaf tler und Mathematiker, Darmstadt, Wiss. Buchges., 1979.