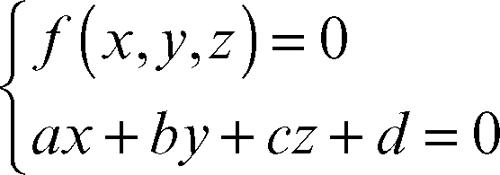piano e superficie, intersezione di

piano e superficie, intersezione di

piano e superficie, intersezione di luogo dei punti dello spazio comuni a un piano e a una superficie assegnati. Tale luogo, se non è vuoto, è costituito da una curva, intesa in senso ampio come varietà algebrica di dimensione 1; in particolare può essere costituito da uno o più segmenti o da una retta o più rette, e varia a seconda della superficie considerata e della reciproca posizione tra piano e superficie. Gli esempi che seguono rappresentano alcuni dei più significativi tra gli innumerevoli casi che si possono considerare (escludendo i casi di intersezione vuota):

• intersezione di un piano e di una sfera: l’intersezione in questo caso risulta una circonferenza, un punto o un insieme vuoto, a seconda che la distanza del piano dal centro della sfera sia minore, uguale o maggiore del raggio della sfera;

• intersezione di un piano e di un cono: considerato un cono indefinito, la curva intersezione è una conica (circonferenza, ellisse, parabola o iperbole a seconda della inclinazione del piano rispetto all’angolo di apertura del cono) e può essere una conica degenere (un punto o due rette eventualmente coincidenti) se il piano passa per il vertice del cono;

• intersezione di un piano e di un cilindro: considerato un cilindro indefinito, la curva intersezione può risultare un’ellisse, in particolare una circonferenza, o un’iperbole degenere costituita da due rette parallele distinte (semplicemente degenere) o coincidenti (doppiamente degenere);

• intersezione di un piano e di un ellissoide: se il piano è parallelo a una coppia di assi dell’ellissoide, ogni intersezione non vuota o è un punto o è un’ellisse;

• intersezione di un piano e di un paraboloide: limitandosi alle intersezioni con piani paralleli o perpendicolari agli assi del paraboloide, si ottengono ellissi o parabole nel caso del paraboloide ellittico, mentre si ottengono iperboli o parabole nel caso del paraboloide iperbolico;

• intersezione di un piano e di un iperboloide: limitandosi a piani paralleli o perpendicolari agli assi dell’iperboloide, si ottengono, sia nel caso dell’iperboloide ellittico sia nel caso di quello iperbolico, ellissi e iperboli;

• intersezione di un piano e di una superficie qualsiasi: la ricerca dell’intersezione tra un piano e una superficie può essere affrontata più in generale con strumenti analitici, definendo tale luogo come insieme di tutti e soli i punti P(x, y, z) soluzioni di un sistema del tipo

avente per equazioni, rispettivamente, l’equazione della superficie e l’equazione del piano (→ piano tangente).