parallelogrammo
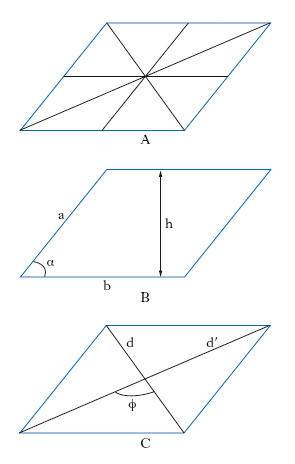
(o parallelogramma) Quadrilatero avente le coppie di lati opposti paralleli. In un p., lati opposti, ovvero angoli opposti, sono uguali, angoli adiacenti sono supplementari; le diagonali sono disuguali (eccetto che nel rettangolo e nel quadrato) ma si tagliano nel loro punto di mezzo che è anche punto di mezzo tra i punti medi di due lati opposti (fig. 1A) e centro di simmetria del parallelogrammo. La somma dei quadrati dei 4 lati è uguale alla somma dei quadrati delle diagonali. L’area A del p. è data dal prodotto della base b per l’altezza h relativa, ovvero dal prodotto di due lati adiacenti a, b per il seno dell’angolo compreso (fig. 1B), cioè A = b h = a b senα; o infine dal semiprodotto delle diagonali per il seno dell’angolo compreso tra esse (fig. 1C), cioè dalla relazione: A = (d d′/2) senϕ.
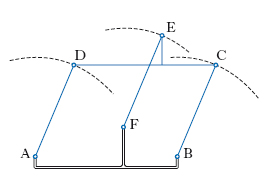
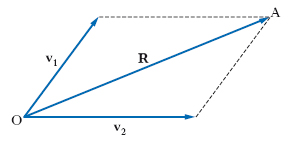
P. articolato Meccanismo costituito da 4 membri a due a due uguali e fra loro paralleli, collegati da 4 coppie rotoidali. Fissato per es. il lato AB (fig. 2), gli altri 2 vertici (C e D) non possono che descrivere circonferenze uguali con centro rispettivamente in B e A e il moto della biella CD è traslatorio. Ogni altro punto E solidale a CD descrive a sua volta una circonferenza uguale a quelle descritte da C e D, con centro F in posizione tale che le figure AFED, FBCE risultino a loro volta parallelogrammi; di conseguenza i punti E e F possono anche essere collegati mediante una manovella. Regola del p. Il risultante di due vettori (O, v1) e (O, v2) è un vettore R (fig. 3) di modulo pari alla diagonale OA del p. (p. dei vettori), avente per lati consecutivi v1 e v2, con origine in O e orientato da O verso A. Se i vettori sono forze, si parla allora di p. delle forze.