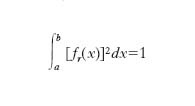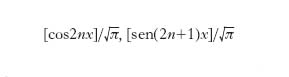ortonormale

In matematica si dice di un sistema di vettori che siano a due a due ortogonali e inoltre di lunghezza unitaria, o anche di un sistema di funzioni f₁(x), … f_n(x), …, in numero finito o infinito, tali che, in un certo intervallo (a, b) dell’asse reale, due qualunque di esse siano ortogonali e inoltre

risulti

,

per r = 1, 2, …

Un sistema o. di funzioni continue si dice poi completo se non è possibile aggregare al sistema un’altra funzione ottenendo un sistema ancora o.; esempi di sistemi o. sono: a) le funzioni

,

per n = 0, 1, 2, … nell’intervallo (0,2π); b) le funzioni (n+1/2)^1/2 P_n(x), per n = 0, 1, 2, … nell’intervallo (−1, 1), dove P_n(x) sono i polinomi di Legendre. L’importanza dei sistemi o. consiste, tra l’altro, nella possibilità, che essi offrono, di rappresentare e individuare un vettore (o una funzione) mediante un certo numero (finito o infinito) di coordinate reali (➔ spazio).

Di particolare interesse è il metodo di Gram-Schmidt per individuare, in uno spazio vettoriale dotato di metrica, una base costituita da vettori o.: siano v₁, v₂, …, v_n, n vettori costituenti una base dello spazio vettoriale V; si ponga e₁ = v₁/| v₁| e si scelga e₂ nel sottospazio generato da v₁, v₂, in modo che sia perpendicolare a e₁ e di lunghezza unitaria; successivamente si prenda e₃ nel sottospazio generato da v₁, v₂, v₃ in modo che sia unitario e perpendicolare ai vettori e₁, e₂ già ottenuti, e così via. I vettori e₁, e₂, …, e_n costituiscono una base o. in V.