nodo

nodo

nodo termine che assume diversi significati a seconda del contesto.

□ In geometria è un punto doppio di una curva algebrica nel quale la curva ha due tangenti distinte; se la curva ha equazioni parametriche x_i = φ_i(t), con i = 1, 2, è il punto che corrisponde a due valori distinti t₁ e t₂ del parametro. Si hanno vari tipi di nodi, a seconda del comportamento delle tangenti: nodo ordinario, tacnodo, oscnodo, flecnodo, biflecnodo ecc.(→ curva, nodo di una).

☐ In teoria dei grafi è così detto ognuno dei vertici di un grafo (→ grafo, nodo di un).

☐ Nelle applicazioni fisiche, è detto nodo ogni punto in cui un sistema di onde stazionarie (come in una corda vibrante o in altri fenomeni vibratori) ha oscillazione nulla.

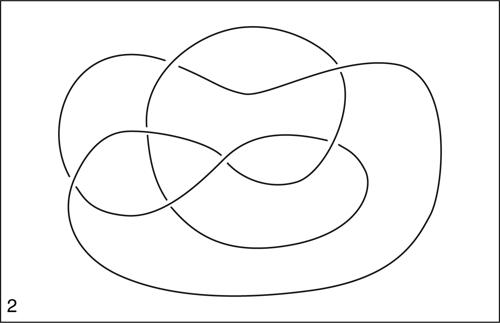
☐ In topologia si formalizza il concetto intuitivo di nodo definendolo come un insieme di punti in R³ omeomorfo a una circonferenza. Un nodo può essere rappresentato graficamente attraverso la sua proiezione su un piano (il piano deve essere scelto in modo che tale proiezione abbia un numero finito di intersezioni con sé stessa). Una rappresentazione di questo tipo si chiama diagramma del nodo. Nei punti in cui la proiezione si autointerseca, detti anche intrecci, il diagramma deve indicare quale ramo del nodo passa sopra e quale passa sotto.

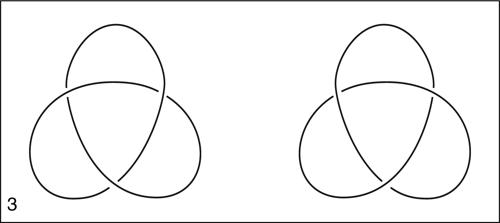
Il nodo più semplice è il nodo “non annodato”, cioè con 0 intrecci, detto nodo banale, raffigurabile banalmente con una circonferenza. I nodi sono classificati in base al numero degli intrecci, ma tale numero non li caratterizza, nel senso che due nodi con lo stesso numero di intrecci possono essere di tipo diverso, giacché non è possibile passare dall’uno all’altro attraverso una deformazione continua, “senza strappi”. Per caratterizzare il tipo di nodo non è perciò sufficiente il concetto di omeomorfismo perché tutti i nodi, essendo omeomorfi a una circonferenza, sono tra loro omeomorfi. Si introduce allora la nozione di isotopia: due omeomorfismi di uno spazio topologico in sé sono detti isotopi se esiste una omotopia che per ogni valore del parametro sia un omeomorfismo. Due nodi sono detti dello stesso tipo o equivalenti quando sono l’uno isotopo dell’altro oppure l’uno è isotopo al simmetrico dell’altro rispetto a un piano. Dal diagramma di un nodo è possibile ricostruire il nodo, a meno di isotopie sulla terza dimensione.

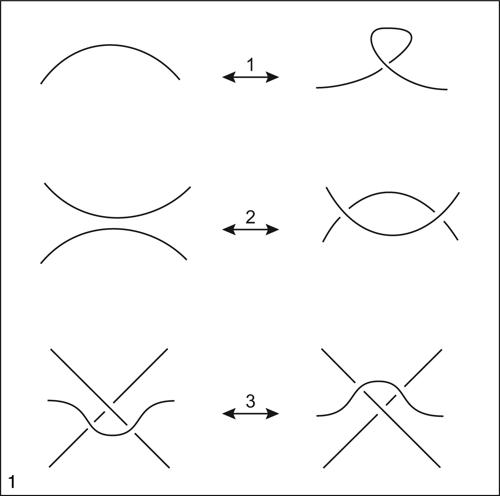
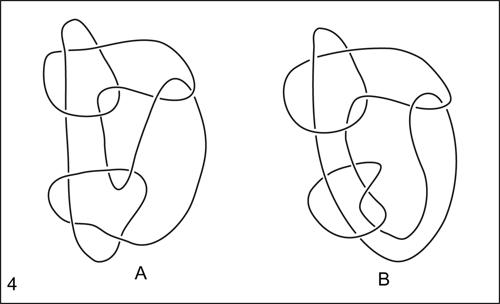
Nel 1926 il matematico tedesco K. Reidemeister dimostrò che due diagrammi di nodi rappresentano nodi dello stesso tipo se è possibile passare dall’uno all’altro mediante isotopie piane oppure tramite uno dei tre seguenti movimenti, detti mosse di Reidemeister: 1) formazione/scioglimento di un ricciolo; 2) scavalcamento/separazione di due tratti di curva non incrociati; 3) scavalcamento di un incrocio da parte di un tratto di curva. Le mosse di Reidemeister permettono di costruire nodi equivalenti a un dato nodo, ma dati due nodi non è determinabile il numero di mosse necessarie per dimostrare che due nodi non sono equivalenti. Non costituendo perciò tali mosse un algoritmo di decisione, la ricerca si è sviluppata nella direzione di determinare invarianti aritmetici e algebrici. È del 1928 l’idea, dovuta al matematico e pacifista statunitense J.W Alexander ii, di associare a ogni nodo un polinomio i cui esponenti sono costruiti a partire dalle particolari caratteristiche degli intrecci e dei loro scioglimenti in base alle mosse di Reidemeister. Per esempio, il cosiddetto polinomio di Alexander del nodo trifoglio N è p_N (t) = t − 1 +t⁻¹. Pur caratterizzando nodi isotopi, i polinomi di Alexander non permettono di distinguere tra un nodo e il suo simmetrico. Ciò è invece possibile con i cosiddetti polinomi di Jones, costruiti nel 1984 da V. Jones, che sono particolari polinomi di Laurent (→ Laurent, serie di), invarianti per isotopia del nodo. Tuttavia anche il polinomio di Jones non è uno strumento di classificazione completo dei nodi perché esiste almeno una coppia di nodi che hanno lo stesso polinomio di Jones ma che sono topologicamente diversi: tale coppia è data dal nodo di Kinoshita e Terasaka e dal nodo di Conway. Una collezione di nodi nello spazio è detta link.

☐ Il nodo è anche un’unità di misura della velocità utilizzata in navigazione, pari a un miglio marino orario (1852 m all’ora).