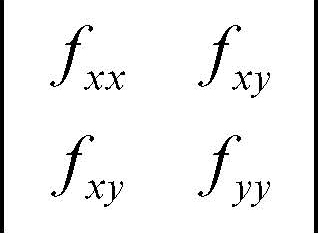curva, nodo di una

curva, nodo di una

curva, nodo di una in termini generali, punto doppio di una curva piana con due tangenti distinte. Intuitivamente è un punto per il quale la curva “passa due volte”. Nello studio delle relazioni definite da un’equazione del tipo ƒ(x, y) = 0, il teorema di Dini della funzione implicita consente di studiare agevolmente il grafico nel caso in cui almeno una delle due derivate parziali ƒ_x o ƒ_y sia diversa da zero. Se tuttavia in un certo punto singolare P₀, soluzione dell’equazione, entrambe le derivate si annullano, è ancora possibile adattare le tecniche di calcolo per ottenere informazioni sul grafico della relazione in un intorno di P₀. Procedendo (in modo euristico) come nel caso regolare, si supponga che la relazione possa esprimersi localmente mediante una funzione y = φ(x), e si derivi l’identità ƒ(x, φ(x)) ≡ 0. Si ottiene dapprima

che in P₀ non dà informazioni in quanto entrambi i coefficienti si annullano. Derivando ulteriormente (nell’ipotesi che tutte le derivate esistano e siano continue) si ha

e dunque, sostituendo le coordinate x₀ e y₀ = φ(x₀) di P₀, si ottiene:

Questa è un’equazione di secondo grado nell’incognita φ′(x₀) e dunque se il discriminante è positivo si avranno due valori reali distinti, corrispondenti a due diverse funzioni φ₁(x) e φ₂(x) i cui grafici nel punto x₀ si tagliano, avendo la stessa ordinata y₀ ma derivate φ′₁(x₀) ≠ φ′₂(x₀). Si noti che il discriminante corrisponde all’opposto del determinante hessiano

calcolato in P₀; dunque se tale determinante è negativo si presenterà quella conformazione particolare che viene detta nodo.

Se ƒ è dotata anche di derivate di ordine superiore, è possibile procedere con tale argomento valutando la derivata φ″(x₀) per ciascuno dei due rami e così per le successive derivate.

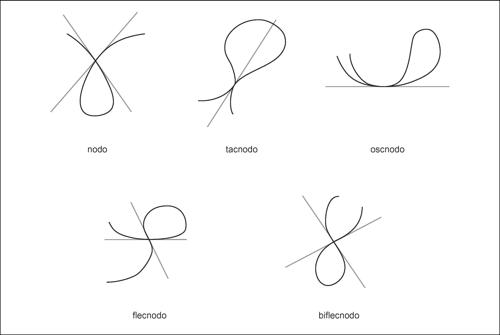
In base alle sue proprietà locali, il nodo può essere classificato nei sottotipi che seguono:

• nodo o punto doppio ordinario: le due tangenti principali sono reali e distinte e hanno entrambe contatto d’ordine 2 con la curva;

• tacnodo: le tangenti principali sono reali e coincidenti e hanno un contatto di ordine 3 con la curva. La curva presenta due rami che hanno tra loro un contatto di ordine 1;

• oscnodo: le tangenti principali sono reali e coincidenti e hanno un contatto di ordine 4 con la curva. La curva presenta due rami aventi tra loro un contatto di ordine 2, perché hanno in quel punto la stessa curvatura;

• flecnodo: le tangenti principali sono reali e distinte e una di esse ha un contatto di ordine 2 con un ramo della curva e molteplicità d’intersezione con la curva uguale almeno a 4;

• biflecnodo: le tangenti principali sono reali e distinte e ciascuna di esse ha un contatto di ordine 2 con un ramo della curva e molteplicità di intersezione con la curva uguale almeno a 4;

• punto doppio isolato: le tangenti principali sono immaginarie e coniugate;

• cuspide o punto di regresso: c’è una sola tangente principale (→ cuspide).