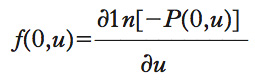Hull-White, modello di

Hull-White, modello di

Modello di arbitraggio per la valutazione di obbligazioni senza cedola, esenti da rischio di insolvenza. Il più noto e utilizzato nella pratica, prende il nome dai due autori che lo proposero all’inizio degli anni 1990: J.C. Hull e A. White. Si basa su un’equazione differenziale stocastica, che descrive l’evoluzione dell’intensità istantanea di interesse a pronti, r(t), in un mondo neutrale al rischio:

dr

=α[γ(t)/α−r(t)]dt+σdW.

Tenuto conto della condizione iniziale r(0)=r_0, la soluzione di tale equazione è:

r

(t)=r₀exp(−αt)+ʃ₀^T[γ(u)exp(α(u−t)du]+ʃ₀^T[exp

(α(u−t))σdW].

Scegliendo

γ

(u)=f′(0,u)+αf(0,u)+(σ²/2α)(1−exp(−2αu)),

è possibile replicare i prezzi osservati sul mercato e, dunque, l’odierna struttura per scadenza dei tassi di interesse (➔ interesse, struttura per scadenza dei tassi di). La notazione

indica l’intensità istantanea a termine desunta dai prezzi spot (➔ prezzo) correnti di obbligazioni di puro sconto. Il modello ha il pregio di poter essere formulato anche in una versione discreta ad albero (➔ albero, metodo ad) trinomiale, che lo rende particolarmente adatto per valutare derivati esotici sui tassi di interesse.