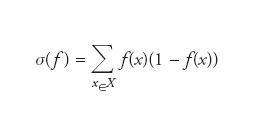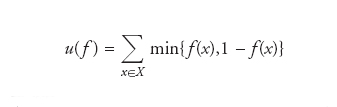misure di fuzziness

misure di fuzziness

Sia ℒ(X) l’insieme di tutti gli insiemi fuzzy f:X→I dove X è un insieme arbitrario e I l’intervallo [0,1] della retta reale. Introduciamo adesso nell’intervallo I=[0,1] la relazione di ordine parziale ≤′ definita, per ogni x, y∈I, come

x ≤′ y ⇔ x ≤ y ≤ 1/2 o x ≥ y ≥ 1/2.

Questa relazione può essere estesa, punto per punto, a ℒ(X) come segue: per ogni f g,∈ℒ(X),

f ≤′g ⇔ ∀x∈X [f(x)≤′g(x)].

Se f≤′g e f≠g diremo che f è più nitido di g.

Possiamo adesso definire le misure di fuzziness introdotte nel 1972. Una misura di fuzziness h è un funzionale h:ℒ(X)→ℝ⁺, dove ℝ⁺ denota i reali non negativi, che soddisfa alcune condizioni che dipendono dal sistema considerato. Gli assiomi base che ogni misura di fuzziness deve necessariamente soddisfare sono i seguenti: (a) h(f)=0 se e solo se f è una funzione caratteristica classica; (b) h(f) raggiunge il suo valore massimo se e solo se f=f ′; (c) h è isotona rispetto all’ordine ≤′, cioè se f≤′g allora h(f)≤h(g). A questi assiomi base se ne possono aggiungere altri come, per es.: (d) h(f)=h(f′), per ogni f∈ℒ(X), cioè una misura di fuzziness assume lo stesso valore su un insieme fuzzy f e sulla sua negazione f′; (e) h è una valutazione sul reticolo ℒ(X), cioè per tutti gli f, g∈ℒ(X),

h(f ∨ g) + (f ∧ g) = h(f) + h(g).

Portiamo adesso due esempi semplici di misure di fuzziness:

[1] formula[2]

Le due misure di fuzziness σ(f) and u(f) così come quella logaritmica soddisfano tutti gli assiomi elencati sopra mentre un esempio di misura che non soddisfa la proprietà di valutazione (assioma e) è data da [σ(f)]². Bruce R. Ebanks ha effettuato uno studio completo del problema della classificazione delle misure di fuzziness con l’aiuto di un ulteriore assioma tecnico (additività generalizzata) dimostrando che l’unica misura che soddisfa tutti i sei assiomi è la σ(f) definita sopra; egli ha poi fornito una caratterizzazione della classe di tutte le misure di fuzziness che soddisfano gli assiomi elencati tranne (d), cioè la simmetria rispetto alla sostituzione di un insieme fuzzy con la sua negazione. Altri studiosi (come Claudi Alsina e Enric Trillas, Chu Kiong Loo, Siegfried Gottwald) hanno studiato particolari forme assunte dalle misure di fuzziness, per es., le condizioni da verificare per ottenere misure che siano valutazioni sul reticolo ℒ(X) e le relazioni esistenti tra le misure di fuzziness, le misure di energia di un insieme fuzzy e la cardinalità generalizzata. Il problema di misurare quanto un insieme fuzzy si allontani da una funzione caratteristica classica è stato affrontato anche in altri modi. Una idea stimolante dovuta a Ronald R. Yager propone di collegarla alla ‘distanza’ tra un insieme fuzzy e la sua negazione, definita usando la nozione reticolare di betweeness. L’idea di Yager fornisce al problema di misurare la fuzziness una nuova interessante visualizzazione, però, non conduce fuori dalle misure ottenibili all’interno dello schema assiomatico delineato prima, perché in tutti i casi in cui è possibile definire una misura alla Yager allora è anche possibile definire una misura di fuzziness nel senso prima descritto.

→ Fuzzy