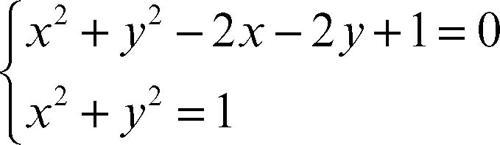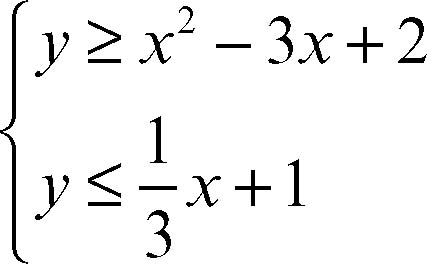metodo grafico

metodo grafico

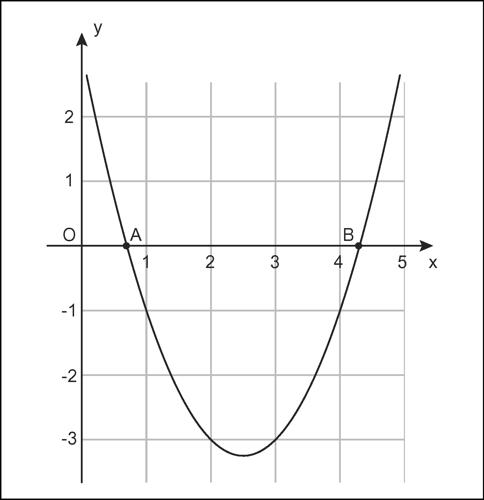
metodo grafico insieme di procedure finalizzate alla risoluzione di equazioni, disequazioni e sistemi, basate essenzialmente sullo studio di proprietà grafiche delle curve che rappresentano le equazioni in gioco. Il metodo permette di ricavare le soluzioni facendo ricorso, in alternativa, alle procedure strettamente algebriche, agli strumenti dell’analisi matematica e dell’analisi numerica. Il caso più semplice è la risoluzione grafica di un’equazione in una incognita, ƒ(x) = 0. In tale caso le soluzioni reali sono rappresentate, graficamente, dalle intersezioni della curva di equazione y = ƒ(x) con l’asse delle ascisse (zeri della funzione). Se ƒ(x) è un polinomio di grado n, le soluzioni reali, contate con la loro molteplicità, sono al massimo n. Per esempio, le soluzioni dell’equazione x ² − 5x + 3 = 0 sono rappresentate dalle ascisse dei punti in cui la parabola y = x ² − 5x + 3 interseca l’asse delle ascisse.

L’equazione ha due radici reali, l’una compresa nell’intervallo (1/2, 1), l’altra compresa nell’intervallo (4, 9/2). In generale, il primo passo consiste nella ricerca di intervalli dell’asse delle ascisse nei quali l’equazione ammette una sola radice dell’equazione ƒ(x) = 0. Tenendo conto di quanto afferma il teorema di esistenza degli → zeri di una funzione, se si individua un intervallo (a, b) ai cui estremi la funzione y = ƒ(x) assume valori di segno opposto e la funzione è continua, allora almeno una radice dell’equazione appartiene a tale intervallo. Se la funzione è derivabile e la derivata ha segno costante in (a, b), la radice è unica nell’intervallo; in caso contrario non si può dire nulla e si procede a restringere l’intervallo e a ripetere le operazioni precedenti o, a seconda dei casi, a fare altre considerazioni ad hoc. Individuato così un intervallo (a, b) in cui la radice è unica, è possibile determinare il valore di quest’ultima o ricavarne un valore approssimato, entro un’approssimazione prefissata, con diversi metodi forniti dall’analisi numerica, tra i quali il metodo di → bisezione, il metodo delle → secanti o il metodo di → Newton con le tangenti.

Per esempio, data l’equazione

dallo studio della funzione

si ricava il suo grafico e si individua (1, 2) come intervallo nel quale si trova un solo zero della funzione. Il valore dello zero è dunque un numero compreso tra 1 e 2. Procedendo con il metodo di bisezione si può stabilire che lo zero è compreso fra 3/2 e 2, poi fra 3/2 e 7/4, e così via. Procedendo con l’algoritmo ci sono due possibilità: o la successione dei valori che esso produce è da un certo punto in poi formata da tutti valori uguali e si ottiene la soluzione esatta, oppure l’algoritmo termina sulla base di un criterio di precisione prefissato e si ha una soluzione approssimata.

Risoluzione grafica di un sistema di equazioni

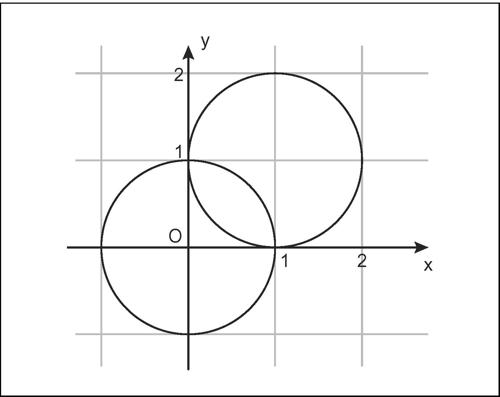
Se per semplicità si considera un sistema di due equazioni in due incognite, la risoluzione grafica di tale sistema consiste nella ricerca dei punti di intersezione delle due curve che rappresentano le equazioni. Per esempio, le soluzioni del sistema

sono date dalle intersezioni di due circonferenze.

Risoluzione grafica di una disequazione

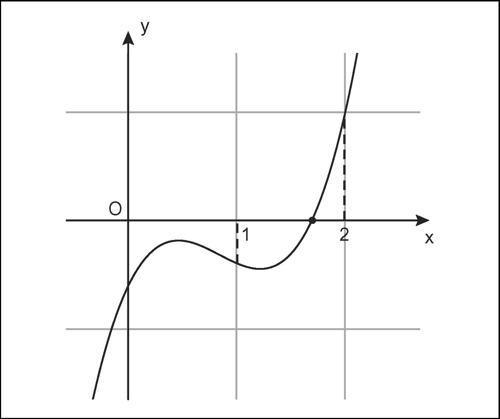
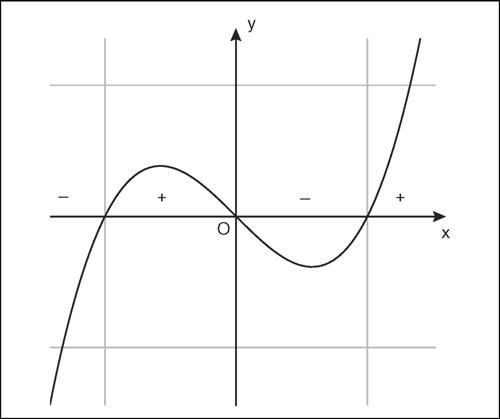
Anche una disequazione in una incognita può essere risolta tramite il disegno del grafico della corrispondente funzione. Per esempio, data la disequazione x ³ − x > 0, si rappresenta la curva di equazione y = x ³ − x, si individuano le soluzioni dell’equazione associata x ³ − x = 0 e infine si ricavano, sull’asse delle ascisse, le zone di positività e di negatività. Dall’esame del grafico si deduce che le soluzioni della disequazione sono costituite dagli intervalli (−1, 0) e (1, + ∞).

Risoluzione grafica di un sistema di disequazioni (in due incognite)

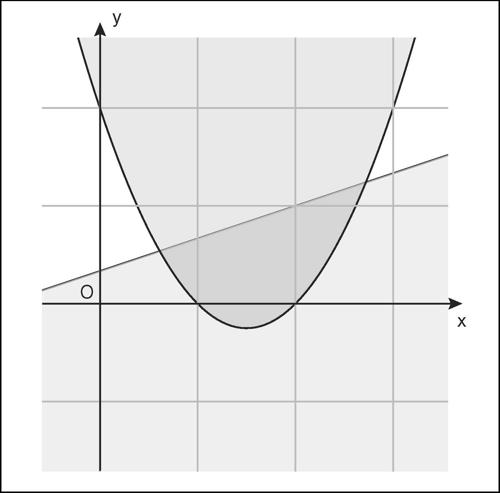
Per risolvere graficamente un sistema di disequazioni in due incognite si considerano opportune regioni del piano cartesiano. Per esempio, dato il sistema

la prima delle disequazioni ha come soluzioni le coordinate dei punti che appartengono alla parabola o sono al suo interno mentre la seconda ha come soluzioni le coordinate dei punti della retta e di quelle dei punti del semipiano che si trova “al di sotto” della retta stessa. Le coordinate dei punti che appartengono all’intersezione delle due regioni di piano sono le soluzioni del sistema. Quanto detto si estende anche a equazioni e disequazioni di altro tipo (irrazionali, goniometriche, esponenziali, logaritmiche ecc.).