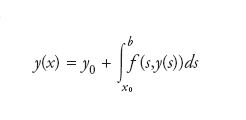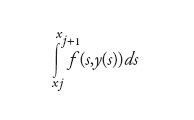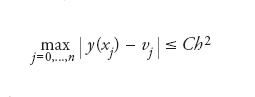metodo dei trapezi

metodo dei trapezi

Metodo numerico per l’approssimazione della soluzione y(x) del problema di Cauchy del primo ordine y′(x)=f(x,y(x)), con x∈(x₀,b) e condizione iniziale y(x₀)=y₀, essendo (x₀,b)⊂ℝ e f:(x₀,b)×ℝ→ℝ una funzione continua sul dominio e uniformemente lipschitziana rispetto alla seconda variabile. Riscriviamo il problema di Cauchy nell’equivalente formulazione integrale

.

.

Il metodo dei trapezi (detto anche di Crank-Nicholson) costruisce la soluzione numerica approssimante y(x) utilizzando la formula di quadratura dei trapezi (ovvero la formula di Newton-Cotes chiusa su due punti). Più precisamente, assegnato un parametro reale h>0, si definisce un insieme di nodi equispaziati e ordinati x=x₀+j∙h ∈ [x₀,b), per j=0,...,n e con n=[(b−x₀)/h], si riscrive l’equazione integrale sull’intervallino [x_ξ,x_ξ+1] e si approssima

con h/2[f (x_ξ, y(x_ξ))+ f (x_{ξ +1}, y(x_{ξ +1}))]. La soluzione numerica ottenuta nei nodi è quindi v_{ξ +1}=v_ξ+h/2[f (x_ξ ,v_ξ)+ f (x_{ξ +1},v_{ξ +1})], per j=0,...,n−1. Questo metodo è stabile per ogni valore positivo di h ed è convergente quadraticamente rispetto ad h, ossia esiste una costante C > 0 indipendente da h tale che

→ Computazionali, metodi