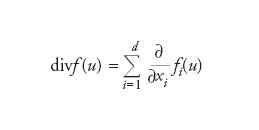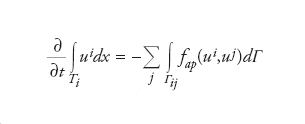metodo ai volumi finiti

metodo ai volumi finiti

Metodo numerico per l’approssimazione della soluzione di un’equazione (o di un sistema di equazioni) alle derivate parziali. Sia Ω un sottoinsieme limitato di ℝ^δ, con d=2,3, e su tale dominio consideriamo, per es., il problema matematico: trovare una funzione u (scalare per semplicità) dipendente dal tempo e dallo spazio, tale che per ogni x=(x₁,…,x_δ)∈Ω e t>0 valga (u/t)+divf(u)=0 (dove f(u) è una funzione vettoriale detta flusso) con u=u₀ assegnata al tempo iniziale t=0 e una opportuna condizione al bordo su tutto Ω oppure su una sua parte a seconda dell’espressione che assume f(u). Osserviamo che ∂/∂t indica la derivata parziale rispetto al tempo mentre

Sia {T} una partizione di Ω in elementi poligonali non sovrapponentisi, ovvero tali che due elementi distinti di {T} possono avere in comune solo lati, vertici e facce e la loro unione ricopre interamente Ω. Integrando la precedente equazione differenziale (che è scritta sotto forma di legge di conservazione) su ogni elemento T_ι di {T} e applicando il teorema della divergenza di Gauss a ogni T_ι, si ottiene la soluzione u del metodo dei volumi finiti come soluzione del sistema di equazioni

dove u^ι=u∣_Τι e u^ξ=u∣_Τξ (generalmente si suppone u^ι costante su ogni T_ι), Γ_ιξ=∂T_ι∩∂T_ξ, la somma è estesa a tutti gli indici j per i quali l’elemento T_ξ è adiacente a T_ι, f_απ(u_ι,u_ξ) è una conveniente approssimazione del flusso normale f(u)∙n su Γ_ιξ e n denota la normale a Γ_ιξ con verso uscente da T_ι. In genere un metodo ai volumi finiti si caratterizza per la forma geometrica degli elementi della partizione, detti volumi di controllo e per come si rappresenta la soluzione u all’interno di ogni volume di controllo. Il metodo ai volumi finiti ha trovato ampia applicazione nella discretizzazione di problemi differenziali in forma conservativa, in particolare quelli che modellano la dinamica dei fluidi.

→ Computazionali, metodi