massimo
massimo
massimo nozione che in matematica ha diverse accezioni.
☐ Per un insieme ordinato (A, ≤) il massimo è un elemento a ∈ A, tale che per ogni x ∈ A risulti x ≤ a. Il massimo può non esistere o perché l’insieme è superiormente illimitato, come la retta reale, oppure perché nessun elemento risulta godere della proprietà richiesta: per esempio, l’intervallo aperto A = (0, 1) non ha massimo, perché per ogni x ∈ A risulta x ≤ 1 ma 1 ∉ A: il punto 1 è invece l’estremo superiore dell’insieme. Naturalmente, ogni insieme finito linearmente ordinato ammette un massimo.
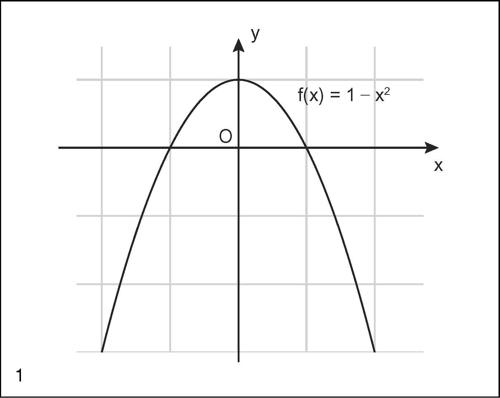
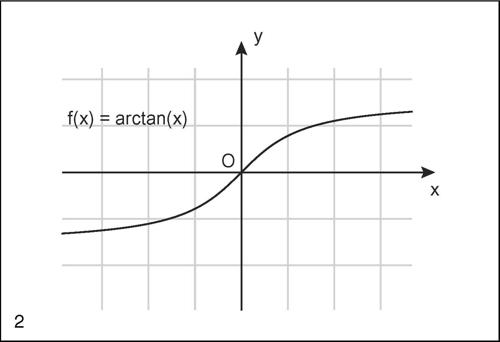
☐ Per una funzione ƒ(x) definita in un insieme E a valori in un insieme ordinato (spesso R o un suo sottoinsieme) il massimo (assoluto) è il massimo del codominio. Per esempio, la funzione ƒ(x) = 1 − x 2 ha codominio (−∞, 1] e 1 è il suo massimo, assunto per x = 0. Invece, la funzione ƒ(x) = arctanx, avendo come codominio l’intervallo aperto (−π/2, +π/2), non ha massimo. I grafici delle due funzioni evidenziano le due diverse situazioni.
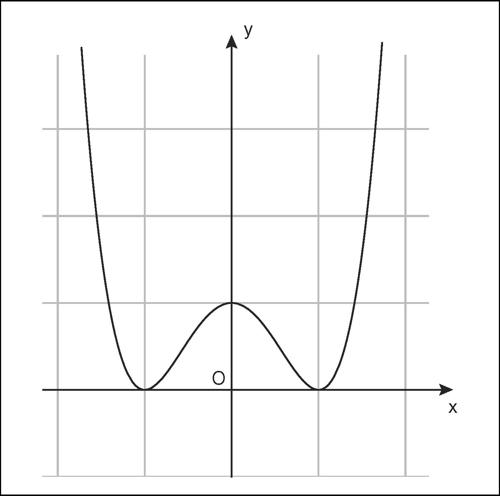
Il massimo può essere assunto in più punti; per esempio, la funzione ƒ(x) = cosx assume il suo massimo valore, uguale a 1, in tutti i punti x = 2kπ, con k ∈ Z. L’aggettivo assoluto può essere tralasciato nell’indicazione di un massimo, salvo quando questo debba essere posto in contrapposizione con un massimo relativo (o locale). Questa nozione è importante in molte questioni applicative e anche dal punto di vista computazionale. Un punto x̄ si dice punto di massimo relativo per ƒ(x) se è di massimo per la restrizione di ƒ(x) a un opportuno intorno U di x̄ e il valore ƒ(x̄) si dice massimo relativo. È dunque ƒ(x̄) ≥ ƒ(x) per ogni x ∈ U ∩ E. Per esempio, la funzione ƒ(x) = (x 2 − 1)2 ha un massimo relativo uguale a 1 in x = 0.
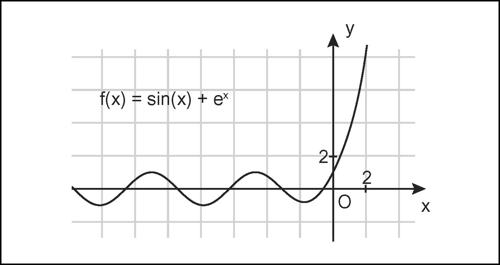
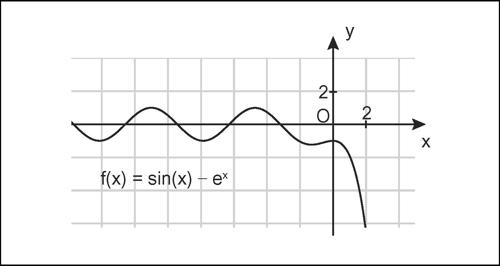
Se una funzione è limitata, il suo massimo assoluto è il maggiore dei massimi relativi, altrimenti una funzione può avere infiniti massimi relativi senza alcun massimo assoluto. Per esempio, la funzione ƒ(x) = sinx + ex ha infiniti massimi relativi nel semiasse x < 0, ma nessun massimo assoluto, perché superiormente illimitata; anche la funzione ƒ(x) = sinx − ex non ha massimo assoluto, pur essendo limitata superiormente essendo ƒ(x) < 1.
La determinazione dei punti di massimo relativo è una delle più importanti applicazioni del calcolo differenziale e anzi tra quelle che hanno dato origine al concetto di → derivata. In un punto x̄ di massimo relativo per ƒ(x), interno a un intervallo (a, b) in cui ƒ(x) è derivabile, risulta infatti ƒ′ (x) = 0; se poi esiste anche la derivata seconda, una condizione sufficiente perché x̄ sia di massimo è che sia ƒ″ (x̄) < 0. Queste condizioni sono soggette alle ipotesi indicate: per esempio, se il massimo è in un estremo di un intervallo [a, b], la derivata prima non si annulla necessariamente, ma deve essere ƒ′ (a) ≤ 0, se il massimo è nel primo estremo, ƒ′ (b) ≥ 0, se è nel secondo. Nulla si può invece dire se la derivata non esiste: per esempio, la funzione ƒ(x) = 1 − |x| ha massimo in x = 0 ma è qui non derivabile. Poiché se una funzione ƒ(x) ammette un massimo in x̄ la funzione −ƒ(x) vi ammette un minimo, quanto sopra detto per i massimi assoluti e relativi si può ripetere per i minimi, cambiando i segni e i versi delle disuguaglianze. In generale, i punti di massimo o di minimo per funzioni derivabili si chiamano punti stazionari (o punti critici). Quanto detto per funzioni di una variabile si estende a n variabili senza alcuna variazione per quanto riguarda le definizioni; per la determinazione della natura dei punti critici in più dimensioni si veda → matrice hessiana.
La ricerca del valore massimo (o minimo) di una grandezza è l’oggetto di un cosiddetto problema di massimo (minimo): per la risoluzione di tali problemi si fa ricorso all’espressione in termini di funzione della grandezza in esame e, quindi, alla ricerca dei suoi punti stazionari, con l’impiego delle derivate. Per esempio, un problema di massimo può essere il seguente: determinare quale dei triangoli isosceli di dato perimetro 2p ha area massima. Per risolverlo, si può indicare un lato obliquo con x e l’area A risulterà funzione di x; la sua espressione è ricavabile dalla formula di → Erone:
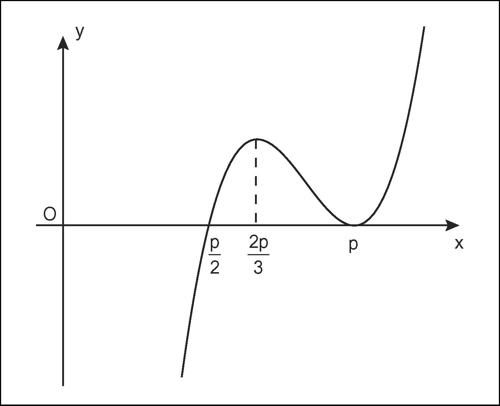
L’area è massima quando lo è il suo quadrato A2(x), la cui derivata si annulla per x = 2p/3 e x = p, come mostra anche il suo grafico. Nel punto M(2p/3, p3/27) la funzione ha un massimo relativo, ma poiché il problema geometrico d’origine è definito per x compreso tra p/2 e p, giacché il lato obliquo di un effettivo triangolo isoscele deve essere maggiore di un quarto del perimetro, tale punto individua un massimo assoluto per il problema in esame. L’area è quindi massima se x = 2p/3, cioè se il triangolo è equilatero (come ci si poteva aspettare per considerazioni legate alla simmetria).
I problemi di massimo e minimo si estendono anche al caso di → funzionali e in tal caso costituiscono l’oggetto del calcolo delle → variazioni.