Magnetismo terrestre

Magnetismo terrestre

Il settore della fisica che si occupa del fenomeno del magnetismo terrestre è denominato geomagnetismo. Dagli anni Sessanta del Novecento sono cambiate notevolmente le tecniche di osservazione e di misurazione (effettuate anche con strumenti portati da veicoli spaziali); alcune di esse hanno messo in crisi procedimenti descrittivi e modelli del geomagnetismo che si ritenevano sufficientemente consolidati. Si sono così verificati, nelle varie sottodiscipline attinenti al campo magnetico terrestre, processi di rinnovamento che hanno dato luogo a un vivace dibattito e che stanno portando a una profonda evoluzione di quella che si può chiamare la filosofia di base della rappresentazione del campo magnetico terrestre. La metrologia geomagnetica, sia per ciò che riguarda la definizione degli elementi del campo sia i procedimenti di misurazione e di elaborazione delle misure, si può ritenere completamente sviluppata già all'inizio del XIX sec., e in tale forma si è mantenuta fino al 1960 circa.

Nel passato l'intensità del campo magnetico terrestre e il valore delle sue componenti erano espresse in unità del sistema CGSem, e precisamente in gauss (G); in ciò la metrologia geomagnetica differiva dall'uso corrente fisico, che utilizzava l'oersted (Oe) e non il gauss (questione puramente nominale, dato che nel vuoto e, con ottima approssimazione, anche nell'aria le misure geomagnetiche nelle due unità CGSem coincidono in valore). Unità corrente, specialmente per le variazioni del campo, era il gamma (γ), pari a 10⁻5 gauss. Con il duplice avvento, alla fine degli anni Sessanta, delle unità del Sistema Internazionale (SI) e dell'induzione in sostituzione dell'intensità come grandezza qualificativa del vettore del campo magnetico terrestre, l'unità geomagnetica di base divenne il tesla (T), con il nanotesla (nT, pari a 10⁻⁹ T) come sottomultiplo corrente. Una felice circostanza è costituita dal fatto che poiché il vecchio gamma e il nuovo nanotesla coincidono in valore e quindi tutte le misure espresse in γ sono direttamente leggibili come espresse in nT, si possono utilizzare, senza alcuna ulteriore elaborazione, gli archivi metrologici geomagnetici del passato.

La frontiera della ricerca nel geomagnetismo è costituita dallo studio dell'origine e delle variazioni del campo principale generato da sistemi di correnti elettriche che scorrono nel nucleo esterno fluido, a una profondità di circa 3000÷5000 km. Le teorie del magnetismo terrestre (magnetofluidodinamica) si basano sulla dinamica del plasma fluido del nucleo terrestre soggetto alle complesse interazioni con la rotazione e i campi di forza terrestri, nonché con i campi radioattivi del Sole, sia elettromagnetici (fotonici) sia particellari.

Tecniche di misurazione degli elementi del campo magnetico terrestre

La scelta degli elementi scalari per definire il vettore del campo magnetico terrestre F fu determinata dagli strumenti al tempo disponibili, che erano basati sull'uso appropriato di un ago magnetico (nella sua forma tipica, un cilindretto di acciaio magnetizzato, lungo ca. 5 cm e del diametro di ca. 5 mm). Lo strumento principale delle misurazioni geomagnetiche fu, a partire dalla metà del XIX sec., il magnetometro ad ago, poi chiamato teodolite magnetico; esso è costituito da un ago magnetico, portato da un filo di sospensione privo di apprezzabile elasticità di torsione, contrappesato in modo da poter ruotare liberamente nel piano orizzontale, che quindi si porta nel piano del meridiano magnetico locale. La direzione dell'ago è quella del Nord magnetico e quindi, con riferimento a una mira da cui dedurre la direzione del Nord geografico, misura indirettamente la declinazione magnetica (D), cosicché lo strumento è di per sé un declinometro magnetico. Munendo tale strumento di un secondo ago magnetico orizzontale (ago deflettore) in posizione fissa ortogonale a una trentina di centimetri dall'ago mobile, dalla posizione assunta da quest'ultimo come posizione di equilibrio tra la coppia dovuta al campo magnetico terrestre e quella dovuta al campo dell'ago deflettore si deduce la misura della componente orizzontale (H), di F. Come terzo elemento scalare era usata l'inclinazione di F sul piano orizzontale (I), che fu misurata in un primo tempo mediante un inclinometro ad ago, costituito da un ago magnetico vincolato in modo da poter ruotare liberamente nel piano verticale del meridiano magnetico locale. Successivamente, fu usato uno strumento più accurato ‒ basato sull'induzione elettromagnetica subita da una piccola bobina piatta fatta ruotare nel campo ‒ e la misurazione dell'assetto dell'asse di rotazione fu effettuata quando la corrente indotta risultava nulla.

Dai valori misurati dei tre elementi D, H, I possono essere ricavati il modulo del campo (intensità totale, F ) e qualsiasi altra componente: in particolare, le tre componenti nel riferimento cartesiano locale con origine nel generico punto di interesse, asse x orizzontale e diretto al Nord geografico, asse y orizzontale all'Est, asse z verticale verso il basso; queste misure rivestono una notevole importanza nel procedimento di analisi armonica del campo. L'accuratezza delle misure ottenute con gli strumenti sopra descritti è elevata: per strumenti da osservatorio, dell'ordine di 1 nT per l'elemento lineare H e di 0,1′(≈3∙10⁻5 rad) per quelli angolari D e I; per le componenti cartesiane dedotte da tali elementi l'accuratezza è di 1 nT per X e Y, ma diminuisce a 4 nT per Z. Accuratezza minore, per un fattore tra 2 e 10, si ha con strumenti portatili, per misurazioni di campagna. Si tratta comunque di strumenti molto costosi e di difficile uso. Negli anni Sessanta e Settanta furono introdotti vari altri strumenti di concezione completamente diversa, in quanto basati su fenomeni fisici di recente scoperta.

fig. 2

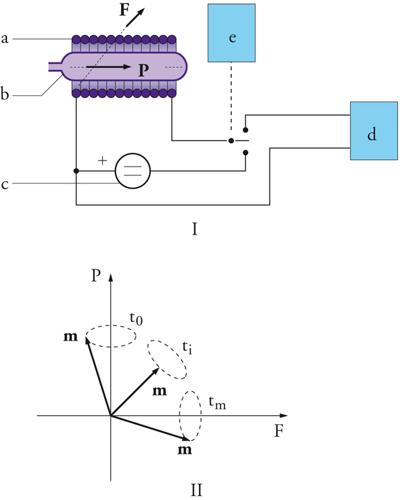
Il magnetometro a precessione nucleare, o a protoni, entrò nell'uso intorno al 1960 e divenne in pochi anni lo strumento principale della geomagnetometria terrestre, cioè per le misurazioni del campo magnetico terrestre effettuate sulla superficie della Terra. Esso è costituito (fig. 2) da un piccolo solenoide rettilineo (bobina), che contiene al suo interno, in un recipiente cilindrico di vetro, un liquido fortemente idrogenato, qual è, tipicamente, l'acqua chimicamente pura, intesa come una sorta di soluzione di protoni (gli ioni H⁺ derivanti dalla dissociazione ionica del liquido), che sono dotati di momento magnetico. Tale sensore viene disposto con il suo asse all'incirca nella direzione est-ovest locale e nella bobina viene inviata per qualche secondo una corrente elettrica continua, che genera un campo magnetico P (campo di polarizzazione) piuttosto intenso (qualche centinaio di volte più intenso del campo magnetico terrestre), il quale orienta (in media) una parte dei protoni parallelamente all'asse della bobina. Interrotta tale corrente, resta attivo il solo campo magnetico terrestre F ortogonale rispetto al precedente campo di polarizzazione; i protoni precedentemente polarizzati sono sollecitati ad allinearsi con la direzione di F.

I protoni si portano su tale direzione non direttamente, ma con un moto di precessione conico intorno a essa; la frequenza della precessione f_p è legata, tramite il rapporto giromagnetico del protone, al modulo F del campo magnetico terrestre, risultando F/f_p=23,4874 nT/Hz; il moto di precessione dei protoni si mantiene come moto d'insieme per pochi secondi (poi le collisioni per agitazione termica fanno venire meno la coerenza) e in questo intervallo di tempo si manifesta ai capi della bobina una tensione indotta alternata misurabile (qualche μV), in quanto ogni protone in precessione equivale a un magnetino lineare che ruoti in un piano contenente l'asse della bobina; in definitiva, la misura di F è facilmente derivabile da quella della frequenza del segnale di precessione, che è misurabile con grande accuratezza, con relativa semplicità e rapidamente (una misurazione dura meno di 5 s) mediante un frequenzimetro elettronico, la cui scala di lettura può essere espressa direttamente in nT. L'accuratezza ottenibile con questo strumento è dell'ordine di qualche decimo di nT, ed è migliore rispetto ai teodoliti magnetici per un fattore compreso tra 2 e 5. Altri vantaggi strutturali sono: le ridotte dimensioni e la piccola massa, che rendono lo strumento trasportabile, la facilità della connessione con un calcolatore per la memorizzazione e l'elaborazione delle misure, e ‒ di primaria importanza ‒ la capacità di misurare facilmente una o più componenti del campo assegnate, il che si ottiene facendo agire sul sensore campi magnetici ausiliari di adeguata intensità e opportunamente diretti, generati da una o più bobine di Helmholtz.

Sfruttando la capacità di misurare una qualunque componente del campo magnetico terrestre, mediante un magnetometro a protoni opportunamente corredato, in vari osservatori magnetici, a partire dal 1974, sono entrati in uso sistematico i cosiddetti magnetometri a precessione completi, che forniscono, in successione automatica ripetitiva, governata da un apposito calcolatore elettronico, l'intensità totale e le tre componenti cartesiane locali. L'accennata ripetitività automatica continua risolve in modo soddisfacente il problema dell'intrinseca discontinuità del magnetometro a precessione dovuta al ciclo di funzionamento descritto in precedenza: la sua durata è tale da consentire una frequenza di circa 4 cicli completi al minuto, ampiamente adeguata per le procedure di routine. Una caratteristica funzionale del magnetometro a protoni, che lo esclude in pratica da utilizzazioni spaziali, è la non trascurabile richiesta di energia elettrica per la corrente generatrice del campo di polarizzazione e dei campi ausiliari per le componenti; così, per misurazioni del campo magnetico terrestre nello spazio circumterrestre a bordo di veicoli spaziali, ci si serve di un altro strumento, il magnetometro a saturazione, detto anche magnetometro flux-gate (letteralmente, a porta di flusso), che ha richieste assai meno onerose per l'alimentazione elettrica.

fig. 6

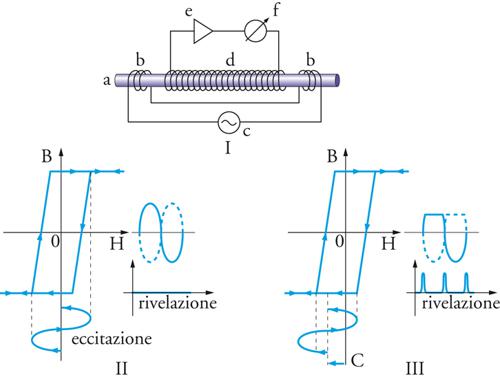
Il sensore di questo strumento è costituito semplicemente (fig. 6) da una piccola bacchetta di ferrite (nucleo magnetico), sulla quale sono avvolte due bobine identiche ma con versi opposti (bobine di polarizzazione), in serie fra loro e collegate a un generatore di corrente alternata (polarizzatore), che determina nel nucleo una magnetizzazione prossima a quella di saturazione, e a una terza bobina (bobina di misurazione), collegata a un amplificatore e a un dispositivo misuratore di tensione alternata (voltmetro). Se sulla bacchetta non agisse alcun campo magnetico esterno, le induzioni B dei campi magnetici alternati ugualmente intensi e antiparalleli generati dalle due bobine di polarizzazione si annullerebbero a vicenda e non si avrebbe una tensione indotta netta nella bobina di misurazione; ma è presente il campo magnetico terrestre F, la cui componente C secondo l'asse della bacchetta va a contribuire alla magnetizzazione di polarizzazione. Semiciclo per semiciclo della corrente di polarizzazione, l'induzione generata da una delle bobine aumenta, determinando la saturazione magnetica, e quella dell'altra bobina diminuisce, per cui nella bobina di misurazione l'insieme del campo polarizzante e di quello terrestre dà luogo a un segnale fortemente asimmetrico, e precisamente di tipo impulsivo, la cui ampiezza media costituisce una misura della componente C del campo magnetico terrestre. Tre di tali sensori, diretti secondo gli assi di un triedro ortogonale, consentono così di avere le misure, continue nel tempo, delle corrispondenti componenti cartesiane del campo. Unico punto di inferiorità rispetto al magnetometro a protoni è l'accuratezza, che nel complesso è almeno 10 volte minore.

Analisi in armoniche sferichedelle misure del campo medio

Il procedimento matematico di elaborazione delle misure del campo medio risale, nella forma tuttora in uso, a Carl Friedrich Gauss. Esso consiste sostanzialmente nel confrontare i coefficienti dei termini di ordine crescente dello sviluppo in serie in coordinate sferiche terrestri, ricavati dagli elementi del campo medio in punti prescelti di determinati paralleli della Terra, supposta sferica (oppure, in moltissimi casi, estrapolati o interpolati da dati misurati in altri punti), con i coefficienti di analoghi sviluppi in serie dei corrispondenti elementi del campo generato da ipotetici dipoli, quadrupoli, ecc., posti nel centro della sfera terrestre (campo interno) oppure al di fuori di essa (campo esterno). Questi coefficienti sono detti di Gauss e sono abitualmente indicati con i simboli g_mⁿ e h_mⁿ per la generica armonica di grado n e ordine m≤n (con n>1 e m>0 numeri interi); il grado è in relazione con la natura della sorgente cui l'armonica si riferisce: n=1 per il dipolo centrale, n=2 per il quadrupolo centrale, e così via. Per esempio, se si indica con a il raggio della sfera terrestre, l'espressione della componente cartesiana orizzontale al Nord è X=k[dP_nⁿ(θ)/dθ][g_mⁿcos(mλ)+h_mⁿsen(mλ)], essendo k una costante dipendente dalle unità di misura adottate, λ la longitudine geografica e P una funzione (funzione modificata di Legendre) della colatitudine geografica θ. Questi coefficienti sono confrontati, in un sistema di equazioni lineari in cui essi sono le quantità incognite, con quelli di un ordinario sviluppo in serie delle misure disponibili, per estrapolazione, per il parallelo prescelto. Da tale confronto si ricavano i valori dei coefficienti di Gauss per le ipotetiche sorgenti dipolari, quadrupolari, ecc., che darebbero luogo al campo realmente osservato, ottenendo per tale via un'immediata informazione sulle sorgenti medesime, in particolare sull'importanza relativa di esse.

Con tale procedimento già a Gauss fu possibile riconoscere che per la quasi totalità il campo magnetico terrestre medio (si considerano sempre valori medi annui) è di origine interna e che di questo campo interno la parte prevalente (oltre il 90%) è quella che sarebbe generata da un dipolo posto nel centro della Terra e con l'asse quasi coincidente con l'asse terrestre: tale campo dipolare centrale fu chiamato campo dipolare o campo di Gauss, identificando in esso il campo geomagnetico principale e attribuendo una natura accessoria, quasi di irregolarità aggiuntive, ai campi rappresentati dalle armoniche di grado maggiore del primo (campi di quadrupolo, ottupolo, ecc.). Questi risultati sono stati sistematicamente confermati dalle analisi successive a quella di Gauss, eseguite su dati dei quali sia il numero sia l'accuratezza sono andati progressivamente crescendo, sia per l'introduzione di magnetometri sempre più sensibili, sia per l'uso di elaboratori elettronici per i lunghi calcoli necessari. Si è verificato però un drastico cambiamento nel considerare come campo principale del magnetismo terrestre il campo dipolare, in seguito all'introduzione, avvenuta intorno al 1981, di una nuova grandezza, la potenza della generica armonica di grado n(R_n) definita dalla relazione R_n=(n+1)∑_m[(g_mⁿ)2+(h_mⁿ)2].

fig. 7

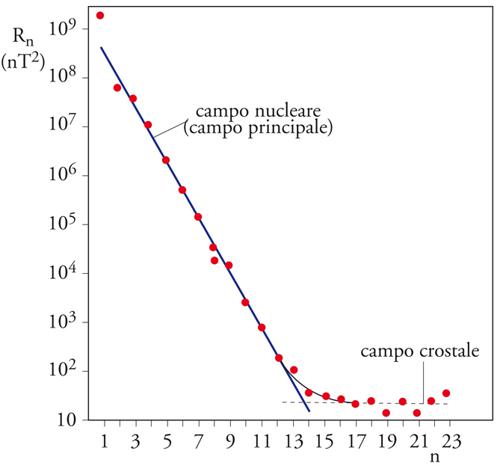
Il diagramma di R in funzione di n per le armoniche interne, cioè rappresentative di sorgenti nella Terra, mostra (fig. 7) che le potenze armoniche sono raggruppate in due gruppi ben distinti, dei quali il primo comprende le armoniche di grado n da 1 a circa 12 e di grande potenza (con una netta prevalenza dell'armonica di grado n=1, cioè del termine di dipolo), i cui punti rappresentativi sono allineati su una retta di notevole pendenza, mentre il secondo comprende, con i punti rappresentativi allineati su una retta di piccola pendenza, le armoniche di grado maggiore di 15, di bassa potenza. Poiché nella Terra la profondità delle sorgenti magnetiche (sistemi di correnti elettriche o di materia magnetizzata) rappresentate da un'armonica, è tanto maggiore quanto minore è il grado dell'armonica medesima, è possibile collegare profondità delle sorgenti e grado delle armoniche.

Da diagrammi del tipo di quello della fig. 7, ottenuti anche adottando per il raggio della superficie sferica di riferimento valori ben diversi da quello del raggio terrestre, si deduce che il campo magnetico medio nel tempo rilevabile sulla superficie terrestre e nello spazio circumterrestre è il risultante di due campi: uno decisamente principale (rappresentato dalle armoniche di grado da 1 a ca. 12), derivante dal sistema di correnti elettriche che scorrono nella parte esterna, fluida, del nucleo terrestre, a profondità tra 2900 e 5200 km, e perciò detto campo nucleare, e un campo assai meno importante e a piccolissima profondità per le armoniche di grado superiore (n>15), le cui sorgenti sono identificabili nelle rocce della crosta terrestre che sono magnetizzate dal campo nucleare, e quindi chiamato campo crostale. Così, si è rivelata erronea la tradizionale concezione che il campo magnetico terrestre effettivo derivi dalla sovrapposizione di campi secondari (di quadrupolo, di ottupolo, ecc.) a un campo principale di dipolo.

Relativamente alla modellistica del campo magnetico terrestre, è da rilevare che il tradizionale modello gaussiano del dipolo centrale come sorgente del campo magnetico terrestre è attualmente usato soltanto per considerazioni di primissima approssimazione e di tipo naturalistico, mentre per rappresentare il campo magnetico terrestre nel suo insieme si usano ora soltanto modelli numerici, costituiti da tabelle dei valori dei coefficienti di Gauss e delle loro derivate temporali prime relativamente a un dato periodo di tempo (di norma 12 mesi), arrestati a un certo grado. La International association of geomagnetism and aeronomy (IAGA), che si occupa, oltre che dell'aeronomia, in primo luogo del coordinamento e della normazione delle ricerche sul campo magnetico terrestre, pubblica ogni cinque anni, a partire dai dati rilevati dalla rete mondiale di osservatori magnetici, un modello numerico di questo tipo fino al grado 10 per i coefficienti e per le derivate temporali prime di essi, detto International geomagnetic reference field (campo geomagnetico di riferimento internazionale) e indicato abitualmente con la sigla IGRF seguita dall'epoca di validità.

Variazioni temporali del campo magnetico terrestre

tab. 1

fig. 8

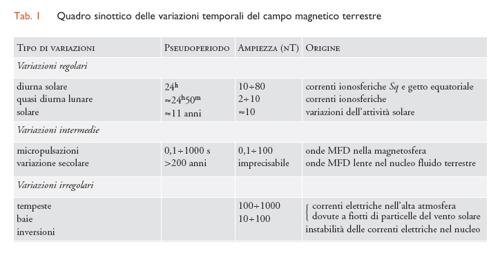
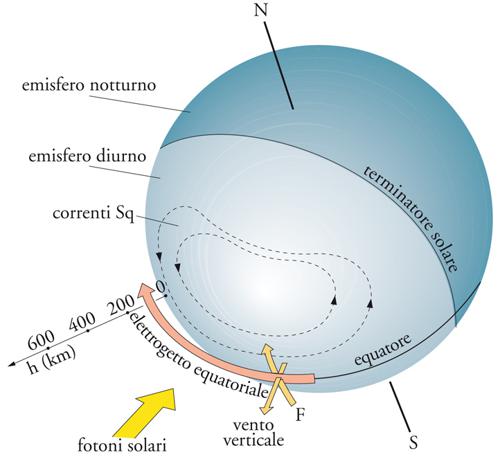
Le variazioni temporali del campo magnetico terrestre, alla luce delle conoscenze attuali, possono essere classificate in tre gruppi principali (regolari, intermedie e irregolari), le cui caratteristiche morfologiche e l'origine sono presentate nella tab. 1. Le variazioni regolari sono pseudoperiodiche in senso stretto; la più importante come ampiezza (qualche decina di nT) è la variazione diurna solare, con uno pseudoperiodo di 24^h, cioè pari alla durata del giorno solare (il periodo della rotazione terrestre). L'analisi in armoniche sferiche mostra che essa è prodotta per circa due terzi da correnti elettriche generate nella ionosfera, a circa 120 km di quota, per interazione tra le correnti e i venti dell'atmosfera, la rotazione terrestre e il campo magnetico terrestre stesso, secondo il meccanismo schematizzato nella fig. 8. Tali correnti dette correnti Sq (Solar quiet current, cioè relativamente ai soli giorni in cui l'attività solare non è agitata), hanno un valore particolarmente intenso lungo l'equatore (corrente elettrica detta elettrogetto equatoriale). Per il restante terzo, invece, tale variazione è ascritta a correnti elettriche indotte nell'interno della Terra dalle stesse correnti che determinano la precedente variazione primaria. Un processo analogo si ha per la variazione quasi diurna lunare, con uno pseudoperiodo di circa 24^h50^m, salvo che per essa vanno considerati moti atmosferici di marea (di qui la minore ampiezza rispetto alla variazione diurna solare). Di grande pseudoperiodo (≈11 anni) è infine la variazione solare, determinata dalla variabilità dell'attività radiativa del Sole.

Le variazioni intermedie si possono considerare una categoria in un certo senso provvisoria, in quanto, mentre appare legittimo includere in esse le micropulsazioni (o pulsazioni) magnetiche, consistenti in treni d'onda pseudoperiodici che si succedono irregolarmente nel tempo e sono dovuti a onde magnetofluidodinamiche (MFD) nella ionosfera e nella magnetosfera terrestri, la stessa cosa non si può dire per la cosiddetta variazione secolare, consistente in lentissime variazioni monotòne degli elementi del campo magnetico terrestre nelle quali non è riconoscibile una qualche pseudoperiodicità. Non va dimenticato che disponiamo di misure geomagnetiche attendibili soltanto da circa due secoli, quindi si potrebbe trattare sia di variazioni con pseudoperiodo maggiore di 200 anni (e pertanto ancora non riconoscibili), sia di variazioni intrinsecamente aperiodiche. Comunque, l'analisi in armoniche sferiche indica per esse un'origine in correnti elettriche nel nucleo fluido terrestre.

Quanto alle variazioni irregolari, quelle di gran lunga più importanti sono le tempeste magnetiche, consistenti in ampie variazioni irregolari decisamente aperiodiche, della durata di qualche giorno, degli elementi del campo; la loro importanza sta anche negli effetti che esse producono in attività umane primarie, quali la navigazione (le bussole magnetiche possono letteralmente impazzire) e le radiocomunicazioni, specialmente quelle con onde corte (che possono interrompersi per parecchie ore). Notevoli perturbazioni sono costituite anche dalle baie magnetiche, che sono variazioni ampie ma più semplici, di durata e ampiezza molto minore di quelle delle tempeste, così dette perché nel diagramma temporale di un elemento del campo si presentano in modo da ricordare una baia sul profilo di una linea costiera. Sia le tempeste sia le baie sono più intense alle alte che alle basse latitudini e sono originate da correnti elettriche nella magnetosfera e nella ionosfera terrestri costituite da fiotti irregolari del vento solare ‒ incessante e irregolare corrente di particelle cariche (elettroni e protoni veloci) che s'irradia dal Sole ‒ deviati verso i poli dal campo magnetico terrestre.

Carattere assolutamente diverso hanno invece le inversioni del campo, che derivano da instabilità del sistema di correnti magnetofluidodinamiche generatrici del campo nucleare. Queste inversioni sono rilevabili e studiabili mediante misurazioni della magnetizzazione propria di campioni di rocce effusive, consolidatesi nei tempi geologici e derivate da colate di vulcani terrestri o da affioramento di fondali oceanici. Tali inversioni si verificano a intervalli di tempo irregolari, dell'ordine di centinaia di migliaia di anni: l'intensità del campo magnetico terrestre diminuisce fino ad annullarsi per poi crescere, ma nel verso opposto, con il polo magnetico Nord che diventa Sud, e viceversa, però senza variazioni altrettanto drastiche della configurazione del campo nel reticolato geografico (si sono avute ca. 250 inversioni negli ultimi 170 milioni di anni e la lenta diminuzione, attualmente osservabile nel valore dell'intensità del campo dipolare, porta a presumere di trovarci in una fase di inversione).

Teorie attuali sull'origine e sulle variazioni del campo magnetico terrestre

Attualmente si ritiene che il campo magnetico terrestre principale si origina dal nucleo fluido (campo nucleare), tra circa 2900 e 5200 km di profondità; a esso si sovrappongono i campi assai meno intensi generati dalle rocce della crosta terrestre magnetizzate dal campo nucleare (campo crostale) e, per la sola parte istantanea, anche da sistemi di correnti elettriche esistenti nell'alta atmosfera terrestre fortemente ionizzata (campo variabile atmosferico, in particolare ionosferico e magnetosferico); tale concezione è più coerente di quelle formulate in precedenza sull'origine del magnetismo terrestre: essa va dunque intesa come origine del campo nucleare. Il campo crostale, infatti, non presenta problemi, in quanto tutte le questioni relative a tale campo, sono ben inquadrate e sviluppate sia nell'ambito della fisica della magnetizzazione della materia, sia nell'ambito della geologia della crosta terrestre.

fig. 9

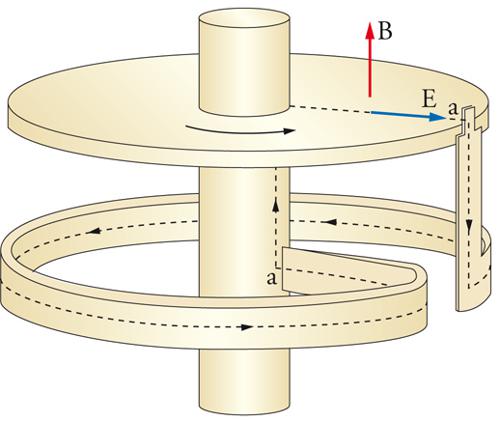
Le teorie sull'origine del campo nucleare furono costrette ad abbandonare il modello elettromeccanico della dinamo geomagnetica ad autoeccitazione di Edward C. Bullard (1949), che destò tante speranze alla sua presentazione (il cui modello è schematizzato nella fig. 9), a causa della scoperta delle inversioni del campo, universalmente accettata soltanto negli anni Cinquanta. Infatti, per giustificare le inversioni occorrerebbe ammettere altrettante inversioni del moto di rotazione della Terra, il che è assurdo. In realtà, per qualche anno, più che di un abbandono si trattò di una serie di tentativi per adattare in qualche modo l'idea base della dinamo terrestre alla realtà del campo autoinvertentesi. Si ricorda, per esempio, il modello di Tsuneji Rikitake (1958), costituito da due dinamo di Bullard di cui l'una alimenta l'altra; si tratta di un sistema intrinsecamente instabile, poiché pur rimanendo tutto in condizioni meccaniche stazionarie (compresi i versi e le velocità di rotazione), il campo magnetico generato s'inverte casualmente e ripetutamente. Tentativi modellistici di questo genere, oltre ad alcuni modelli astratti derivati di tipo vettoriale, furono però alla fine effettivamente abbandonati. Ci si spostò nell'ambito, arduo ma ineccepibile, della dinamica del plasma fluido del nucleo terrestre soggetto alle complesse interazioni con la rotazione terrestre e i campi di forza terrestri (il campo gravitazionale, il campo di gradiente termico e lo stesso campo magnetico), nonché con i campi radiativi del Sole, sia elettromagnetici (fotonici) sia particellari: nacque così l'impostazione magnetofluidodinamica delle teorie del magnetismo terrestre.

I fatti da spiegare restano i seguenti: (a) il campo magnetico terrestre è un campo debole (induzione dell'ordine di 5 10⁻5 T) quasi dipolare, con momento magnetico pressoché parallelo all'asse terrestre, vecchio all'incirca come la Terra; (b) attualmente, il campo magnetico terrestre decresce in intensità per circa un 5% a secolo, precede verso ovest (deriva occidentale) in ragione di circa 2° a secolo per la parte dipolare e di circa 10 volte tanto per la parte non dipolare, e inverte spesso e casualmente il suo verso. Le assunzioni di base sono: (a) il nucleo esterno della Terra è un plasma molto caldo e denso (ma con densità di carica elettrica locale identicamente nulla), elettromagneticamente lineare, con temperatura fra 2700 e 3200 K, pressione fra 1 e 3,5 1011 Pa (cioè fra 1 e 3,5 milioni di volte la pressione atmosferica al suolo), con conduttività elettrica σ non nulla e, a causa dell'alta temperatura, con permeabilità magnetica che può essere assunta pari a quella del vuoto, μ0; (b) il nucleo partecipa al moto della rotazione terrestre e in esso si sviluppano moti convettivi a causa della presenza di un forte gradiente termico radiale.

Le equazioni di Maxwell dell'elettromagnetismo e l'equazione di Navier-Stokes della fluidodinamica forniscono le seguenti prima e seconda equazione della magnetofluidodinamica (MFD, detta anche magnetoidrodinamica o MHD):

[1] ∂B/∂t=(μ0σ)−1∇2B+rot(v×B)

[2] ∂v/∂t=−ϱ−1(∇p−j×B−A)−2 (ω×v)+(μ0σ)−1∇2v

essendo B l'induzione del campo magnetico (il vettore F del campo magnetico terrestre), t il tempo, ∇ l'operatore vettoriale nabla, v la velocità del plasma, ϱ la densità (massa volumica), p la pressione, ω la velocità angolare (di rotazione della Terra), j la densità di corrente elettrica nel plasma, A ogni altra forza agente sul plasma. La [1] è la forma che in questo caso prende la terza equazione di Maxwell dell'elettromagnetismo, mentre la [2] non è altro che l'equazione fondamentale della dinamica (massa per accelerazione uguale alla forza agente), dove i termini del secondo membro rappresentano, nell'ordine, la forza di pressione, la forza di Lorentz, ogni altra forza di natura diversa dalle altre qui nominate, la forza di Coriolis, quella di attrito ‒ la quantità (μ0σ)⁻1 si chiama, per analogia, viscosità magnetica ‒ agenti sull'unità di massa del plasma.

La risoluzione di queste equazioni per il plasma del nucleo terrestre presenta notevoli difficoltà di calcolo, che non sono state ancora completamente risolte. Soluzioni di tipo euristico, ottenute mediante opportune semplificazioni, mostrano che a seguito dei moti, reciprocamente ortogonali, di rotazione e convettivi, nel nucleo si destano correnti di plasma di tipo circolare; se inizialmente nel nucleo è presente un campo magnetico, anche di debole intensità, che abbia una componente non nulla secondo l'asse della rotazione terrestre, le correnti di plasma sono risolte in un sistema di correnti elettriche elicoidali, tali che il campo magnetico generato da esse rinforza il campo iniziale fino al raggiungimento di una situazione di equilibrio tra le energie attive e passive in gioco, cui corrisponde la costanza del campo magnetico. Gli studi in corso sulla risoluzione incondizionata delle equazioni della magnetofluidodinamica nell'ambito geomagnetico sono volti specialmente a dare conto, ipotizzando qualcosa sulla non omogeneità elettromagnetica del nucleo terrestre, delle irregolarità sia temporali sia geografiche del campo magnetico terrestre evidenziate dalle misure; in particolare, sembra che le inversioni e la deriva occidentale possano essere spiegate in modo soddisfacente con l'ipotesi della formazione di onde magnetofluidodinamiche di grandissimo periodo e piccola velocità nel nucleo terrestre.

Bibliografia

Jacobs 1987-1991: Jacobs, John A., Geomagnetism, London, Academic Press, 1987-1991, 4 v.

Molina 1993: Molina, Franco, Magnetismo terrestre, in: Enciclopedia delle scienze fisiche, Roma, Istituto della Enciclopedia Italiana, 1993, III, pp. 534-545.

Per i valori correnti degli elementi degli Osservatori magnetici italiani, v. l'Annuario magnetico, pubblicato dall'Istituto Nazionale di Geofisica di Roma.