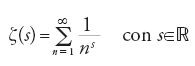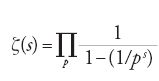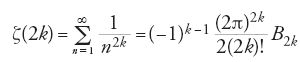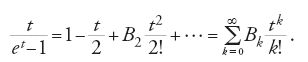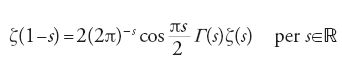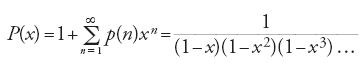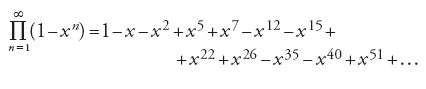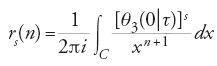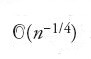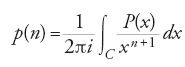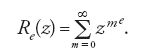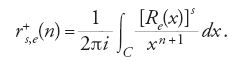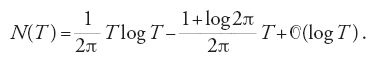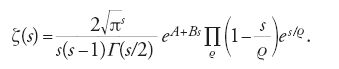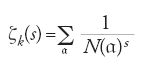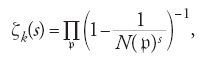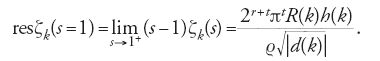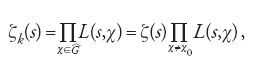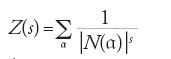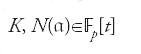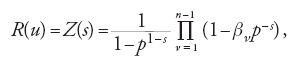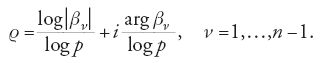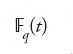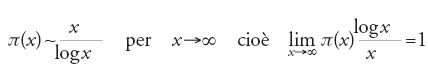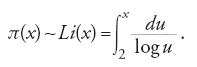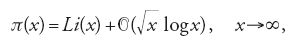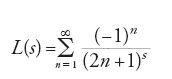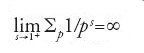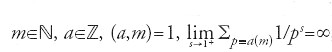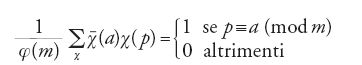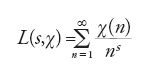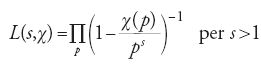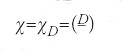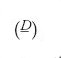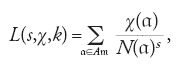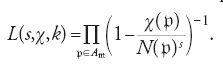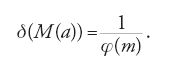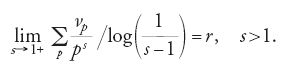La seconda rivoluzione scientifica: matematica e logica. Teoria analitica dei numeri
La seconda rivoluzione scientifica: matematica e logica. Teoria analitica dei numeri
Teoria analitica dei numeri
La teoria analitica dei numeri non è una teoria matematica ben definita, nel senso che non è costruita su assiomi o definizioni, né vi sono metodi o teoremi generali e unificanti. In linea di massima essa comprende quella parte della teoria dei numeri nella quale, per definire e dimostrare certe particolari proprietà, l'analisi e i passaggi al limite hanno un ruolo essenziale. I metodi aritmetici, algebrici, analitici e geometrici sono importanti nella teoria moderna; per questa ragione la teoria analitica dei numeri ha molte parti in comune con discipline come la teoria algebrica dei numeri, la geometria algebrica, la teoria dei campi di funzioni, dei gruppi, delle algebre, con l'analisi p-adica, la geometria e la teoria delle probabilità, per citare soltanto le più importanti. Non vi è di conseguenza una netta separazione tra ciò che appartiene alla teoria analitica dei numeri e ciò che non vi appartiene. Vi è tuttavia un principio generale al quale si ricorre spesso per molti problemi: esso consiste nell'associare a funzioni aritmetiche funzioni analitiche, come le funzioni ellittiche o modulari, alle quali è possibile applicare il teorema di Cauchy o l'analisi armonica. Inoltre, nella teoria analitica additiva dei numeri il metodo del cerchio e quello del crivello forniscono un principio generale per alcune particolari classi di problemi.
Leonhard Euler (1707-1783) fu il primo ad applicare sistematicamente metodi analitici per ottenere proprietà dei numeri interi. Una delle funzioni più importanti per lo studio delle proprietà dei numeri è la funzione ζ da lui introdotta nel 1737 nell'articolo Variae observationes circa series infinitas, pubblicato nel 1744:
Euler dimostrò, facendo uso del teorema fondamentale dell'aritmetica sull'unicità della fattorizzazione in numeri primi, che ζ(s) ammette una rappresentazione come prodotto infinito:
dove il prodotto è esteso a tutti i numeri primi, e s>1 è un numero reale. Se si fa tendere s a 1+ si dimostra che esistono infiniti numeri primi in quanto la serie armonica ∑1/n è divergente. Prendendo il logaritmo del prodotto infinito Euler dimostra però un risultato molto più forte, e cioè che già la serie ∑1/p è divergente, cioè lim ∑1/ps=∞ per s che tende a 1+, dove la somma è estesa a tutti i numeri primi.
Per la relazione contenuta nel prodotto [2], la funzione ζ è strettamente legata alla teoria moltiplicativa dei numeri. Questa si occupa sia di problemi relativi alla fattorizzazione in fattori primi, sia degli stessi numeri primi, intesi come mattoni che permettono di costruire la fattorizzazione. Dopo aver calcolato nel 1735 ζ(2k) per k naturale, Euler scoprì nel 1739 il legame con i numeri di Bernoulli:
dove i numeri di Bernoulli B2k erano stati definiti da Euler come i coefficienti della serie:
Si ha così B0=1, B1=−1/2, B2=1/6, B3=0, B4=−1/30, B6=1/42, B8=−1/30, B10=5/66, … (e Bk=0 per k dispari e maggiore di 2).
I numeri di Bernoulli sono numeri razionali e hanno un ruolo importante anche nella teoria algebrica dei numeri. Nel 1735 Euler calcolò anche il valore ζ(2k+1) per k naturale, cioè per i numeri naturali dispari, senza tuttavia fornire una formula esplicita. Nel 1749 egli scoprì però la cosiddetta equazione funzionale:
Questa fondamentale relazione fu dimostrata nel 1859 da Georg Friedrich Bernhard Riemann (1826-1866). Egli considerò ζ(s) come una funzione complessa (cioè con s numero complesso), e dimostrò tramite l'equazione funzionale [5] che ζ(s) si può estendere all'intero piano complesso e che è meromorfa con un solo polo in s=1, semplice e di residuo 1. Riemann avanzò numerose importanti congetture su ζ(s), che ebbero una notevole influenza sullo sviluppo della teoria analitica dei numeri.
Un altro campo nel quale Euler introdusse metodi analitici fu la teoria delle partizioni: in tal modo problemi appartenenti alla teoria additiva dei numeri venivano affrontati in modo analitico. La teoria delle partizioni si occupa del numero p(n) dei modi di scrivere un numero naturale n come somma di una successione non crescente di numeri naturali; per esempio, 5=4+1=3+2=3+1+1=2+2+1=2+1+1+1= =1+1+1+1+1. Si ha quindi p(1)=1, p(2)=2, p(5)=7, e così via. Questo problema fu trattato nelle Observationes analiticae variae de combinationibus del 1741, e ripreso più dettagliatamente nel cap. 16 della Introductio in analysin infinitorum (pubblicato nel 1748 ma scritto nel 1744) e nel lungo lavoro De partitione numerorum (1750, continuato nel 1768). Questi trattati aprirono la strada a importanti rami della teoria analitica dei numeri, come il metodo del cerchio di Hardy, Littlewood e Ramanujan (1918), la funzione η di Dedekind (1877), la teoria delle funzioni modulari, e anche ad applicazioni delle funzioni ellittiche alla teoria dei numeri (per es., a opera di Carl Gustav Jacob Jacobi dal 1829 in poi). Euler trovò una stupefacente quantità di identità riguardanti p(n). Fondamentale tra queste è la rappresentazione come prodotto della funzione generatrice P(x) della funzione di partizione p(n):
Questa identità fu utilizzata da Hardy e Ramanujan (1918) per determinare una espressione asintotica di p(n).
Il lavoro di Euler del 1741 contiene anche un primo esempio di serie θ, e cioè:
Euler osservò subito che gli esponenti di questa serie contengono i numeri pentagonali n=(1/2)k(3k±1), con il segno + se k è pari e il segno − se k è dispari. In sostanza, egli scopriva così la formula del prodotto per la forma modulare ∑(−1)k x[k(3k+1)]/2 ove k varia fra −∞ e +∞.
La [7] fu dimostrata la prima volta da Euler in una lettera a Christian Goldbach (1690-1764) nel 1750. Più tardi Jacobi avrebbe costruito la sua teoria delle funzioni ellittiche (1829) sull'idea di Euler relativa alle serie con esponenti appartenenti a una progressione aritmetica del secondo ordine. Si sarebbero sviluppati in tal modo nuovi metodi analitici per lo studio delle proprietà dei numeri interi.
Teoria additiva
La teoria additiva dei numeri si occupa di problemi riguardanti l'espressione di un dato intero n quale somma di un tipo particolare di interi, come quadrati, potenze maggiori o numeri primi, e in quanti modi ciò sia possibile.
Somma di quadrati
Il problema più antico di questo tipo è la rappresentazione di un numero naturale in somma di due, tre e quattro quadrati.
Condizioni per la rappresentabilità come somma di quadrati. Condizioni per la somma di due quadrati furono ottenute da Carl Friedrich Gauss (1777-1855) nel 1801 come conseguenza della teoria generale delle forme quadratiche binarie, dovuta allo stesso Gauss. La condizione è la seguente: un intero positivo n è somma di due quadrati, n=x2+y2 con x e y interi, se e solo se i fattori primi q di n della forma q=4k+3 compaiono con esponente pari.
Nel caso della somma di quattro quadrati un contributo importante fu dato da Joseph-Louis Lagrange (1736-1813) il quale nel 1770 dimostrò una congettura che risaliva a Diofanto: ogni intero positivo n è somma di al più quattro quadrati, n=x2+y2+z2+t2, con x,y,z,t interi.
Una forma più precisa del teorema dei quattro quadrati fu ottenuta da Adrien-Marie Legendre (1752-1833) che nel 1785 e nel 1798 trovò la condizione necessaria per la somma di tre quadrati: un intero positivo n è somma di al più tre quadrati, n=x2+y2+z2 con x,y,z interi se e solo se n≠4r(8t+7) dove r e t sono interi non negativi.
La parte difficile da dimostrare è la sufficienza di questa condizione: essa fu dimostrata nel 1801 da Gauss che utilizzò la teoria del genere delle forme quadratiche binarie.
Numero di rappresentazioni come somma di quadrati. Sia rs(n) il numero delle rappresentazioni di un numero naturale n come somma di s quadrati di interi. Lagrange nel 1773 e Gauss nel 1801 dimostrarono, per la somma di due quadrati, che:
[8] r2(n)=4[d1(n) - d3(n)],
dove da(n) denota il numero di divisori t di n della forma t=4k+a. Nel 1829 Jacobi utilizzò, per dimostrare questo risultato, un'identità per funzioni ellittiche e funzioni θ. Con il medesimo metodo analitico egli aveva determinato nel 1828 anche il numero delle rappresentazioni di n come somma di quattro quadrati: r4(n) è uguale a 8 o 24 volte la somma dei divisori dispari di n, a seconda che n sia dispari o pari.
Nel 1896 il matematico tedesco Adolf Hurwitz (1859-1919), facendo uso della teoria aritmetica dei quaternioni interi, diede una nuova dimostrazione di questo risultato con metodi algebrici.
Per quanto riguarda il numero delle rappresentazioni primitive r′3(n) di n come somma di tre quadrati, Gauss derivò nel 1801 una formula esplicita in termini del numero delle classi e del genere di forme quadratiche binarie primitive di discriminante −n o −4n, e Leopold Kronecker (1823-1891) trovò, nel 1850, un'espressione per r3(n) usando funzioni ellittiche. Tuttavia il problema di determinare tutte le rappresentazioni di interi positivi n come somma di esattamente tre interi non nulli non è ancora completamente risolto: esso dipende infatti dalla determinazione di tutti i cosiddetti 'numeri idonei'.
Nel periodo 1870-1950 si ottennero numerose formule per rs(n), per s≥5, ma anche per s=2,3,4, soprattutto per mezzo di funzioni ellittiche e funzioni θ. Esse si basano sulla scoperta di Jacobi che rs(n) è il coefficiente di xn=eπinτ nello sviluppo di Taylor della funzione θ:
dove θ(x)=θ3(0∣τ) converge per ∣x∣⟨1. Si può rappresentare rs(n) per mezzo dell'integrale di Cauchy
dove C è il cerchio di centro l'origine e raggio r⟨1 (con r vicino a 1).
Nel 1916 Srinivasa Ramanujan (1887-1920) applicò le funzioni modulari allo studio di rs(n), e poco tempo dopo Louis J. Mordell (1888-1972) riuscì a trattare il problema in modo piuttosto generale con queste funzioni, prima nel caso s pari (1917) e quindi anche per s dispari (1919). Lo strumento più potente è però il metodo del cerchio, introdotto da Godfrey H. Hardy (1877-1947). Per calcolare rs(n), il cerchio C dell'integrale di Cauchy [10] viene suddiviso in archi secondo la successione di Farey (partizione di Farey), e il contributo delle singolarità dell'integrale di Cauchy dovute ai punti razionali viene attentamente e abilmente calcolato. Questi metodi furono ulteriormente sviluppati principalmente da John E. Littlewood, Hans Rademacher e Harold Davenport. Carl Ludwig Siegel e Rademacher li estesero successivamente ai campi di numeri algebrici.
Teoria delle partizioni
Hardy e Ramanujan applicarono le loro tecniche anche alla teoria della funzione p(n), che è legata alla rs(n). Nel 1917 essi dimostrarono un teorema di tipo tauberiano per determinare il comportamento asintotico di log p(n). Nel 1918 ottennero uno sviluppo asintotico di p(n) con un termine di errore
per mezzo della funzione generatrice di Euler P(x) della funzione di partizione p(n) data dalla [6]. P(x) è una funzione olomorfa per ∣x∣⟨1, connessa alla funzione modulare η di Dedekind. La p(n) si può rappresentare mediante l'integrale di Cauchy:
dove C è un cerchio di centro l'origine e raggio r⟨1 (con r vicino a 1). Come nel caso di rs(n), la nuova fondamentale idea di Hardy per calcolare p(n) è il metodo del cerchio: prendere archi del cerchio determinati da successioni di Farey e studiare il contributo delle singolarità dell'integrale di Cauchy dovute ai punti razionali del cerchio. Con un raffinamento del metodo del cerchio, Rademacher riuscì nel 1937 a determinare una formula esatta per p(n) come sviluppo in serie convergente. Nel 1942 Paul Erdâs (1913-1996) fornì una dimostrazione elementare del comportamento asintotico di p(n), e nel 1941 Albert E. Ingham (1900-1967) pubblicò un teorema molto generale di tipo tauberiano sulle partizioni. Ramanujan enunciò una serie di congetture sulle proprietà di congruenza di p(n), come, per esempio:
se 24n;1 mod 5n, allora p(n);0 mod 5n
se 24n;1 mod 7n, allora p(n);0 mod 7[(n12)/2]
se 24n;1 mod 11n, allora p(n);0 mod 11n,
dove [(n12)/2] è il massimo intero ≤(n12)/2. Queste congruenze furono dimostrate da George N. Watson (1938) e da A.O.L. Atkin (1967) utilizzando le funzioni modulari.
Il problema di Waring
Il teorema di Lagrange dei quattro quadrati spinse Edward Waring (1734-1798) a congetturare nelle Meditationes arithmeticae (1770) quello che è ora noto come teorema di Waring: (1) ogni numero naturale n è somma di al più 9 cubi (non negativi); (2) ogni numero naturale n è somma di al più 19 quarte potenze; (3) per ogni esponente e.1 esiste un (minimo) numero naturale s5s(e) tale che ogni numero naturale n è somma di al più s potenze e-esime (non negative).
Per i teoremi di Lagrange dei quattro quadrati e di Legendre dei tre quadrati, il minimo s5s(e) per l'esponente e52 è s5s(2)54. Waring non riuscì a dimostrare il suo teorema. David Hilbert (1862-1943) dimostrò nel 1909 il punto 3 e la sua dimostrazione fu semplificata da Robert Remak (1912) ed Erik Stridsberg (1916). Una dimostrazione elementare fu ottenuta da Linnik nel 1943. Che effettivamente sia s(3)59 fu dimostrato da Arthur Josef Alwin Wieferich (1909) e Aubtey J. Kempner (1912), e che s(4)519 da Ramachandran Balasubramanian, François Dress e Jean-Marc Deshouillers solo nel 1987. Jing-Run Chen ha dimostrato nel 1964 che s(5)537, mentre Siva Sankatanarayana Pillai aveva stabilito nel 1935 che s(6)573.
Come nel caso della somma di quadrati e delle partizioni, una generalizzazione del metodo di Jacobi permise a Hardy e Littlewood (1920-1928) di ottenere stime del numero
di soluzioni in interi non negativi xi dell'equazione
xe1+xe2+…+xes=n,
con n numero naturale. Essi utilizzarono la funzione:
Questa serie converge per ∣Z∣<1, e
si può esprimere con l'integrale di Cauchy:
Il metodo del cerchio di Hardy fornisce informazioni sul numero
di soluzioni, anche se le approssimazioni sono più difficili da calcolare che non nel caso delle partizioni. Per tale ragione il metodo di Hardy e Littlewood fu integrato con nuove idee come quelle di Ivan Matveeviã Vinogradov (1934) e Hermann Weyl. Siegel (1944, 1945) studiò una versione generalizzata del problema di Waring per campi di numeri algebrici, introducendo ulteriori nuove tecniche.
La congettura di Goldbach
In una lettera a Euler del 1742 Goldbach avanzò le seguenti congetture: (1) ogni numero pari n.4 è somma di due numeri primi dispari; (2) ogni numero n.1 è somma di (al più) tre numeri primi; (3) ogni numero dispari n.1 o è primo, oppure è somma di tre primi dispari.
È chiaro che i punti 2 e 3 seguono dal primo. Nel rispondere a Goldbach Euler affermava di credere fermamente nella congettura, ma di non essere in grado di dimostrarla. A oggi (2004) la congettura non è stata ancora dimostrata, anche se risultati parziali sono stati ottenuti grazie ai nuovi metodi, in particolare quello del cerchio di Hardy-Littlewood (1919). Basandosi su questi metodi Vinogradov dimostrò nel 1937 che ogni numero dispari sufficientemente grande è somma di (al più) tre numeri primi.
Egli dimostrò che r(n),n2/2(logn)3, dove r(n) denota il numero delle rappresentazioni di n come somma di tre primi, utilizzando a questo scopo il teorema dei numeri primi per progressioni aritmetiche per stimare il corrispondente integrale sugli archi maggiori. Hardy e Littlewood avevano ottenuto lo stesso risultato nel 1923, ma sotto l'ipotesi che la L-serie L(s,χ) per un carattere χ non avesse zeri nella regione
Nel 1955 T. Tatuzawa stabilì il teorema di Vinogradov per campi di numeri algebrici.
Inoltre, per quanto riguarda il punto 1 della congettura di Goldbach, Johannes Gualtherus van der Corput, Theodor Estermann e Nikolaj Grigor9eviã Ãudakov nel 1938 dimostrarono indipendentemente che quasi tutti i numeri pari, cioè tutti escluso un insieme di densità zero, sono somma di due numeri primi.
I metodi di crivello
In relazione alla congettura di Goldbach e al problema dei numeri primi gemelli, Viggo Brun (1885-1978) sviluppò, tra il 1915 e il 1924, il metodo di crivello, generalizzando un'idea che risale a Eratostene (ca. 284-200 a.C.). Brun dimostrò inoltre che il numero dei primi gemelli {p,p12} minori di n è dell'ordine di n/log2n, deducendo da qui che la somma degli inversi dei numeri primi gemelli converge. Nel 1947 Atle Selberg sviluppò ulteriormente il metodo di crivello e nel 1941 Jurij Vladimiroviã Linnik (1915-1972) inventò il 'grande crivello' applicando il metodo di crivello a classi di congruenza.
Con il metodo di Linnik, Chen ottenne nel 1966 il notevole risultato che vi sono infiniti primi p tali che p12 ha al più due fattori primi. Egli arrivò molto vicino alla dimostrazione della congettura di Goldbach, quando provò che ogni numero pari sufficientemente grande è somma di un primo e di un intero che ha al più due fattori primi.
Teoria analitica moltiplicativa
Questa teoria tratta le proprietà analitiche connesse con la fattorizzazione in numeri primi. Al centro dello studio vi è la funzione ζ, in particolare la formula del prodotto di Euler [2], l'equazione funzionale [5], il suo comportamento nel suo unico polo e molte generalizzazioni ed estensioni di questi concetti.
Funzioni ζ. Congettura di Riemann
Funzione ζ di Euler. Nel fondamentale lavoro del 1859 Riemann estese la funzione ζ(s) di Euler a valori complessi di s, mostrando come essa si possa estendere a tutto il piano complesso ℂ, che è meromorfa in ℂ con un solo polo in s=1, semplice e di residuo 1, e che non ha zeri nel semipiano Re(s)>1. Riemann enunciò inoltre sei importanti congetture su ζ(s) basate sull'equazione funzionale [5]. Tra queste vi sono le tre seguenti, tutte relative agli zeri di ζ(s).
Congettura 1. Se ζ(s)=0 per un numero complesso non reale s=a+ib, allora a=1/2, vale a dire tutti gli zeri non reali di ζ(s) giacciono sulla retta verticale Re(s)=a=1/2. (Gli zeri reali, o banali, sono dati da s=-2,-4,…,-2n,…, e sono tutti semplici).
Congettura 2. Se N(T) denota il numero di zeri di ζ(s) nel rettangolo aperto R(T):0<Re(s)<1,0<Im(s)<T, allora N(T) è dato dalla formula asintotica:
Congettura 3. La funzione ζ(s) ammette la seguente rappresentazione come prodotto di Weierstass esteso agli zeri complessi s=ρ di ζ(s):
La congettura 2 fu dimostrata nel 1895 e nel 1905 da Hans von Mangoldt (1854-1925) che dimostrò anche un'altra delle sei congetture. Nel 1893 Jacques Hadamard (1865-1963) dimostrò la congettura 3. La congettura 1, nota come ipotesi di Riemann, è ancora oggi uno dei più importanti problemi irrisolti della matematica.
Riemann dimostrò che ζ(s) ammette infiniti zeri non banali e che questi si trovano tutti nella striscia critica 0<Re(s)<1. Nel 1914 Hardy riuscì a dimostrare che vi sono infiniti zeri sulla retta critica Re(s)=1/2, un risultato già provato da Riemann in un manoscritto non pubblicato.
Edward C. Titchmarsh nel 1936 trovò che vi sono 1041 zeri nel rettangolo R(1468), e che si trovano tutti sulla retta Re(s)=1/2. Per studiare la distribuzione dei valori di ζ(s) Harald Bohr (1887-1951) introdusse nel 1925 la teoria delle funzioni quasi periodiche.
La funzione ζ di Dedekind
Per lo studio delle proprietà moltiplicative di un campo di numeri algebrici k, e in particolare del numero delle classi di questo, Richard Dedekind (1831-1916) introdusse nel 1871 la funzione ζ di k:
per s∈ℂ, Re(s)>1, e dove
denota la norma di a, per a che varia tra gli ideali interi di k.
La funzione di Dedekind ζk ha proprietà simili a quelle della funzione ζ di Euler; in particolare Dedekind dimostrò nel 1879 che (1) ζk(s) è assolutamente convergente per Re(s)>1; (2) ζk(s) ammette una formula prodotto (grazie al teorema fondamentale dell'aritmetica di Dedekind sulla fattorizzazione unica degli ideali in un campo di numeri algebrici):
prodotto esteso a tutti gli ideali primi p di k; (3) ζk(s) ha un polo semplice in s=1.
Particolarmente importante è la formula analitica del numero delle classi data dal residuo di ζk(s) in s=1:
Questa formula, fondamentale, collega tutti gli invarianti importanti del corpo di numeri k, e cioè il discriminante d(k), il regolatore R(k) e il numero delle classi h(k) di k, e inoltre il numero r di radici dell'unità di k, il numero r di immersioni reali e il numero t di coppie di immersioni complesse coniugate di k in ℂ.
Edmund Landau (1877-1938) dimostrò nel 1903 che ζk(s) si può estendere analiticamente a Re(s)>1-1/n, dove n è il grado di k su ℚ, ed Erich Hecke (1887-1947) dimostrò nel 1917 che ζk(s) soddisfa un'equazione funzionale dalla quale egli ricavò che ζk(s) è una funzione meromorfa nel piano complesso con un singolo polo in s=1, che è semplice. Il teorema di Landau aprì la strada alla dimostrazione del teorema dei numeri primi per i campi di numeri algebrici. In una lettera a Ferdinand Georg Frobenius dell'8 luglio 1896 Dedekind dimostrò che sussiste la fondamentale relazione tra la funzione zeta di Dedekind ζk(s) di un'estensione abeliana k su ℚ (contenuta nel campo ciclotomico delle radici m-esime dell'unità) e la funzione zeta di Euler ζ(s) vista come la funzione zeta di Dedekind del campo base ℚ:
dove
è il gruppo dei caratteri modulo m o un suo sottogruppo, o anche (dal punto di vista della teoria dei corpi di classe) il gruppo dei caratteri del gruppo di Galois G di k/ℚ, e c0 è il carattere principale.
La relazione [19] fu ottenuta per la prima volta da Dedekind nel 1879 nel caso in cui k è il p-esimo campo ciclotomico, p primo. Nel caso di un campo di numeri quadratico k=ℚ(√D) era già nota a Peter Gustav Lejeune Dirichlet (v. la [33]). Teiji Takagi (1875-1960) la dimostrò nel 1920 nel caso generale in cui K/k è un'estensione abeliana di un campo di numeri algebrici. Che zK(s)/zk(s) sia una funzione intera se K/k è un'estensione normale di un campo di numeri algebrici è stato dimostrato da Hiroshi Aramata nel 1933, basandosi sul lavoro di Artin sulle funzioni L dello stesso Artin. La dimostrazione fu semplificata da Richard D. Brauer nel 1947 ed ebbe una notevole influenza sulla dimostrazione della congettura di Siegel riguardante una generalizzazione della formula del limite dello stesso Siegel. L''ipotesi generalizzata di Riemann', formulata da Pierre Piltz verso il 1884, afferma che gli zeri non reali di ζk(s) si trovano sulla retta Re(s)=1/2. Gli zeri reali sono di ordine r+t per s=-2,-4,…,-2n,…, di ordine t per s=-1,-3,…,-2n+1,….
La funzione ζ di Artin
Nella sua tesi del 1921 Emil Artin (1898-1962) iniziò lo studio delle estensioni quadratiche
del campo delle funzioni razionali Fp(t) a coefficienti in un campo primo finito Fp. Per studiare il numero delle classi di questi campi Artin introdusse una 'funzione z' per K, la funzione:
per s complesso, dove la somma è estesa a tutti i divisori interi a di
è la norma di a, e
se
è di grado n e p denota il numero di elementi di Fp. Artin dimostrò molte proprietà di Z(s), analoghe a quelle della funzione ζ di Euler, in particolare la formula del prodotto, l'equazione funzionale e la formula del numero delle classi. Dimostrò che Z(s) è una funzione razionale R(u) di u=p−s, che si può esprimere come prodotto esteso ai propri zeri:
dove b1,…,bn−1 sono le radici di un'equazione algebrica a coefficenti razionali zn−11s1zn−21…1sn−150 e z5u−15ps. Gli zeri r di Z(s) sono dati da pr5bn, per n51,…,n21, ossia:
L'ipotesi di Riemann per K(√D), cioè Re(ρ) uguale a 1/2, è equivalente alla relazione log ∣βν∣=1/2 log p, o anche ∣βν∣=√p, per ν=1,…, n-1. Essa equivale anche ad affermare che le radici di R(u)=0 si trovano sul cerchio ∣u∣=p−1/2 poiché Re(s)=1/2 corrisponde a ∣u∣=p−1/2. Dal 1925 in poi, Friedrich Karl Schmidt estese la teoria di Artin a una qualunque estensione algebrica K di grado finito su
con q=pν. Helmut Hasse (1898-1979) nel 1933 riuscì a dimostrare l'ipotesi di Riemann nel senso di Artin nel caso in cui K è un campo di funzioni ellittiche, e André Weil (1906-1998) nel 1948, basandosi su propri lavori e su quelli di Hasse riuscì a estendere il teorema di Hasse a ogni campo K di grado finito su
Teorema dei numeri primi
Legendre (1785) fu il primo a trovare un'approssimazione (non proprio corretta) per il numero p(x) dei numeri primi minori di x, dove x è un numero reale. Dopo molti calcoli (fino a x=3.000.000), Gauss congetturò intorno al 1792 che:
Questa congettura, nota oggi come teorema dei numeri primi, fu dimostrata per la prima volta da Riemann (1859) sulla base delle sue congetture sulla sua funzione ζ. Nel 1896 Hadamard e Charles de la Vallée-Poussin (1866-1962) riuscirono a dimostrare indipendentemente il teorema dei numeri primi senza usare l'ipotesi di Riemann. Il punto cruciale era dimostrare che per la funzione ζ di Euler, si ha ζ(s)=0 per s=1+ib, dove b è un qualunque numero reale. Soltanto dopo i lavori di Hardy negli anni 1920-1930 e di Norbert Wiener (1894-1964) negli anni 1927-1933 risultò chiaro che questa condizione era in realtà l'unica essenziale e che era equivalente al teorema stesso. L'ipotesi di Riemann, che z(s)=0 per Re(s)>0 implica s=1/2+ib, afferma in realtà qualcosa di molto più forte, e quindi implica il teorema dei numeri primi. Gauss, in una lettera del 1849 a Encke indicava che
Nel 1900 Hilbert osservò che l'ipotesi di Riemann era equivalente alla:
che dà la migliore maggiorazione possibile. Landau dimostrò nel 1908 che:
con un'esplicita costante positiva c, un risultato ottenuto anche da de la Vallée-Poussin nel 1899. L'esponente di e fu migliorato da Vinogradov nel 1958. Gauss aveva congetturato che π(x)<Li(x), ma Littlewood dimostrò nel 1914 che π(x)-Li(x) cambia di segno infinite volte.
Una dimostrazione elementare del teorema dei numeri primi (senza usare metodi dell'analisi) fu trovata indipendentemente da Selberg ed Erdâs nel 1949. Selberg dimostrò che θ(x)=∑log p∼x, dove la somma è estesa a tutti i primi minori o uguali a x. Questo risultato è equivalente al teorema dei numeri primi. La funzione θ(x) era stata introdotta da Pafnutij L´vovič Čebyšev (1821-1894) nel 1848 per dimostrare la congettura di Bertrand (1845), che afferma che esiste almeno un primo tra n e 2n, n.1.
Nel 1853 Čebyšev aveva congetturato anche che esistono, in un certo senso, più primi della forma 4k+3 che della forma 4k+1; più precisamente:
Nel 1914 Hardy, Littlewood e Landau dimostrarono che la congettura di Čebyšev equivale ad affermare che gli zeri complessi della funzione L (del carattere non principale modulo 4):
si trovano sulla retta Re(s)=1/2, un caso particolare dell'ipotesi di Riemann.
Funzioni L. Primi in progressione aritmetica
Funzioni L di Dirichlet. Dirichlet generalizzò nel 1837 la formula [2] di Euler e la sua dimostrazione ‒ e cioè che
(la somma è estesa a tutti i numeri primi p), e quindi che vi sono infiniti primi ‒ alle classi di congruenza modulo un intero m>1 per dedurne che: se a è un intero primo con m, esistono infiniti primi p tali che p≡a (mod m).
Dirichlet si propose di dimostrare, seguendo le idee di Euler, che per
ovvero che ∑p≡a(m)1/p diverge.
Egli dovette introdurre molte nuove idee. Innanzi tutto occorreva identificare i primi p congrui ad a mod m, e ciò si poteva ottenere introducendo i caratteri χ modulo m. La teoria generale dei caratteri dei gruppi sarà però sviluppata solamente più tardi da Dedekind, nel 1879.
Secondo Dedekind, un carattere di Dirichlet c modulo m è una funzione che associa a un intero a primo con m una radice m-esima dell'unità, in modo che: (1) χ(a+m)=χ(a); (2) χ(ab)=χ(a)χ(b), per ogni intero b. Si pone inoltre: (3) χ(b)=0 se b non è primo con m. Molto importanti sono le relazioni di ortogonalità:
dove
denota il carattere complesso coniugato di χ e φ(m) la funzione di Euler. Dirichlet introdusse poi per ogni carattere χ modulo m le serie L di Dirichlet:
con s∈ℝ e s>1. Si tratta di funzioni ζ generalizzate. Infatti, se χ0 è il carattere principale che assegna il valore 1 agli a primi con m, allora L(s,χ0)=ζ(s) a meno di un fattore costante dipendente da m. Più precisamente, L(s,χ0)=∏p∣m(1-1/ps)ζ(s). Per questi motivi le funzioni L hanno proprietà simili alle funzioni ζ. In particolare, Dirichlet dimostrò che esse soddisfano la proprietà del prodotto di Euler:
Inoltre, L(s,χ) converge per Re(s)>0 se χ non è il carattere principale. Dirichlet utilizzò poi il metodo di Euler di prendere il logaritmo della formula del prodotto ed esprimere la somma che ne risulta come una somma doppia infinita su tutti i primi. Per ottenere il contributo dei primi congrui ad a modulo m, egli moltiplica questa somma per il carattere complesso coniugato, prende la somma su tutti i caratteri, e applica le relazioni di ortogonalità. Il problema si riduce così a dimostrare che log L(1,χ) è finito se χ≠χ0, cioè che
[32] L(1,χ)≠0 se χ≠χ0.
Il punto cruciale è allora dimostrare che L(1,χ)≠0 se χ è un carattere reale non principale, cioè per χ tale che χ2=1 ma χ≠χ0. Un tale carattere è un carattere quadratico
per un certo D dipendente da m, dove
denota il simbolo quadratico di Kronecker. Questa parte richiede ancora una nuova idea, e cioè stabilire un legame con il numero delle classi h(D) del campo quadratico ℚ(√D), più tardi individuato da Weber come il legame tra il campo delle classi e il carattere quadratico
Tale legame è dato dalla formula di Dirichlet:
dove c(D) è una costante non nulla che dipende dal discriminante e dalle unità del campo ℚ(√D). Da ciò consegue L(1,χD)≠0. Il teorema della 'formula analitica del numero delle classi' espresso dalla [33] era già noto a Gauss. Siegel lo applicò allo scopo di dimostrare che logh(D)∼log∣√D∣, se D→−∞ e che logh(D)logεD∼log∣√D∣, se D→+∞, dove εD è l'unità fondamentale di ℚ(√D). Da queste formule sui limiti si possono dedurre alcune congetture di Gauss sul numero delle classi di un campo di numeri quadratico o sulle forme quadratiche binarie. Dedekind osservò che il prodotto tra L(s,χD) e L(s,χ0) è essenzialmente la sua funzione ζk(s) del campo di numeri quadratico k=ℚ(√D). Generalizzando tali idee ai campi ciclotomici, Dedekind riuscì a ottenere la formula analitica del numero delle classi di Kummer per campi ciclotomici e la relazione [19].
Funzioni L di Weber di un campo di numeri algebrici. Combinando la teoria di Dirichlet delle funzioni L modulo m e quella di Dedekind della funzione ζ di un campo di numeri algebrici, Heinrich Martin Weber (1842-1913) si propose, nel 1897, di dimostrare l'analogo del teorema di Dirichlet sui primi in progressione aritmetica per un campo k di numeri algebrici. Seguendo Dirichlet, Weber introduce per un ideale intero m di k la serie L (di Weber):
dove la somma è estesa a tutti gli ideali interi a di Am, cioé all'insieme degli ideali frazionari di k primi con m, e χ è un carattere del gruppo quoziente Cm=Am/Hm, dove Hm è un sottogruppo di indice finito di Am contenente tutti gli ideali principali di k. Weber scrive χ(a)=χ([a]) se [a] è la classe di a in Cm.
Si ha la rappresentazione di Euler come prodotto:
Nell'ipotesi che gli ideali interi di k siano ugualmente distribuiti tra le classi di Cm, e che esista un campo di numeri K su k che soddisfi le due condizioni seguenti: (1) il grado ν=[K:k] è minore o uguale dell'ordine h di Cm; (2) ogni ideale primo p di Hm di grado 1 si spezza completamente in K in ideali primi di grado 1, Weber fu in grado di dimostrare che L(1,χ,k)≠0 se χ≠χ0, e quindi di dedurre che ogni classe di ideali [a]∈Cm contiene infiniti ideali primi di grado 1. Ottenne inoltre la proprietà che allora ν=h. Weber chiamò 'corpo di classe' di Cm un campo K che soddisfa le proprietà (1) e (2). Takagi dimostrò nel 1920 che un tale corpo esiste sempre, che è unico, e che ha molte importanti proprietà. In particolare, le proprietà aritmetiche di k si riflettono in proprietà del gruppo di Galois G di K su k, che è abeliano e isomorfo a Cm. Hecke dimostrò nel 1917 che le funzioni L di Weber soddisfano un'equazione funzionale, e che sono funzioni intere nel piano complesso ℂ.
Funzioni L e legge di reciprocità di Artin. Nel 1923 Artin introdusse, per un'estensione normale K/k di campi di numeri, le cosiddette funzioni L di Artin L(s,χρ,K/k), dove ϱ è una rappresentazione del gruppo G di Galois di K/k e il carattere cr è la traccia della matrice che corrisponde a r. Artin congetturò che le funzioni L di Weber L(s,c,k) coincidessero con le sue funzioni L nel caso in cui K/k è un'estensione abeliana. Questa congettura è equivalente alla 'legge di reciprocità' di Artin per estensioni abeliane, che afferma che esiste un isomorfismo esplicito tra il gruppo di Galois G e il gruppo delle classi di congruenza Cm, che corrisponde a K per via della teoria dei corpi di classi di Takagi e su cui i caratteri χ di Weber sono definiti. Artin dimostrò questa legge di reciprocità nel 1927 dopo aver visto un lavoro di Nikolaj Grigor'evič Čebotarev (1894-1947) sulla densità degli ideali primi.
La congettura di Artin, secondo cui le funzioni L sono funzioni intere se c non è il carattere principale, è uno dei grandi problemi ancora aperti.
Funzioni L di Kornblum. In un lavoro del 1913 (pubblicato nel 1918) Heinrich Kornblum (1890-1914) introdusse i caratteri χ modulo M e le funzioni L(s,χ) modulo M per il campo di funzioni di congruenza
,
dove M è un polinomio in
Se χ non è il carattere principale c0 allora L(s,χ) è un polinomio in u=p−s di grado inferiore al grado di M. La funzione L(s,χ0) è l'analogo della funzione ζ di Euler. Ha un polo semplice di ordine 1 in s=1.
Seguendo Dirichlet, Kornblum stabilì le proprietà fondamentali di queste funzioni L, in particolare la proprietà del prodotto di Euler, e che L(1,χ)≠0 se c non è il carattere principale. Da queste egli dedusse l'analogo del teorema di Dirichlet sui primi in progressione aritmetica.
Densità dei primi
Per stabilire criteri per l'irriducibilità dei polinomi, Kronecker introdusse nel 1880 quella che Hilbert (1897) chiamerà 'densità' e Hasse, più correttamente 'densità di Kronecker', per insiemi di primi. Essa si basa sul comportamento della funzione ζ(s) nel suo unico polo s=1, semplice e di residuo 1, cioè tale che
Prendendo il logaritmo del prodotto di Euler [2] che rappresenta ζ(s) si ha ∑p1/ps∼log 1/(s-1), e ciò dà luogo alla definizione di Kronecker: se M è un insieme di numeri primi, allora
è la 'densità (di Kronecker)' di M. Le proprietà della funzione ζ implicano che δ(M)=1 se M e l'insieme di tutti i numeri primi. Se M è finito, δ(M)=0, e viceversa se δ(M)>0 M è infinito. Se si suppone che i numeri primi siano uniformemente distribuiti tra le φ(m) classi di congruenza modulo un numero naturale m che sono prime con m, il metodo di Dirichlet implica che, se M(a) denota l'insieme dei primi p della forma p=mx1a con a primo con p, allora:
Ciò dipende dal fatto che L(s,χ)≠0, se c è un carattere di Dirichlet modulo m diverso dal carattere principale c0. Viceversa, la [37] implica che L(s,χ)≠0 per χ≠χ0. Landau studiò, nel 1903, la 'densità naturale' ∆(M) di M definita come
dove p(x) e il numero dei primi minori di x e μ(x) quello dei primi minori di x appartenenti a M. Dimostrò che se ∆(M) esiste, anche δ(M) esiste e sono uguali. Il contrario però non è sempre vero. Il teorema principale di Kronecker è: se
è un polinomio a coefficienti interi, r il numero di fattori irriducibili di F(x) in Z[x] e νp il numero di soluzioni di F(x)≡0 modulo p per un numero primo p, allora:
Da tale risultato Kronecker dedusse un fondamentale teorema sulla fattorizzazione di F(x) in Z[x]: se Mk è l'insieme dei primi p per cui F(x)≡0 modulo p ha k soluzioni modulo p e Dk=δ(Mk) è la densità di Kronecker di Mk, e se
è di grado n e ha r fattori iriducibili in Z[x] allora:
Kronecker enunciò molte proprietà notevoli delle densità Dk. Per es., se
è irriducibile e di grado n, allora esistono infiniti numeri primi p tali che F(x) si spezza completamente in n fattori lineari modulo p. In alcuni casi egli dette indicazioni per le dimostrazioni. Alcune proprieà furono dimostrate da Frobenius nel 1896; molte però restano aperte. Kronecker sottolineò che Dk dipende soltanto dal gruppo di Galois G di F(x), in particolare dal sottogruppo A=(Sn:G) di G. Che le densità Dk esistano realmente fu dimostrato da Frobenius solo nel 1896. Egli enunciò anche un teorema di densità per i numeri primi rispetto alle classi di coniugio di G, vale a dire per quei primi per i quali F(x) si spezza in un dato modo modulo p. Egli dimostrò il teorema di densità nel caso in cui il gruppo di Galois G di F(x) è il gruppo simmetrico Sn (teorema di densità di Frobenius). Il caso generale fu dimostrato da Čebotarev nel 1925 (teorema di densità di Čebotarev). Tale dimostrazione ispirò Artin per quella della legge di reciprocità.