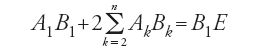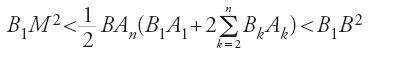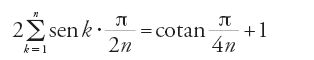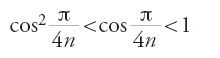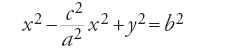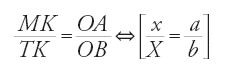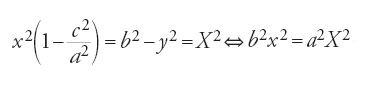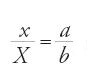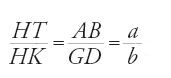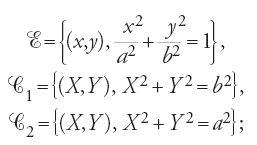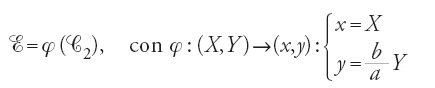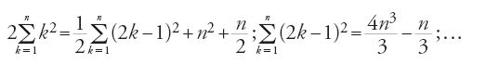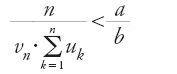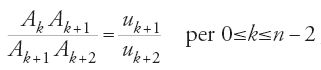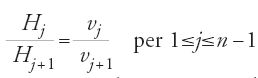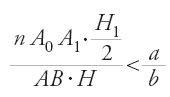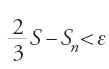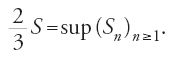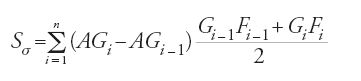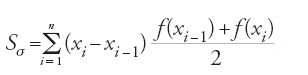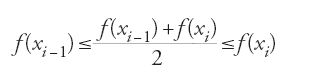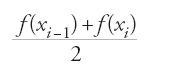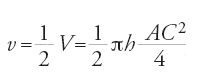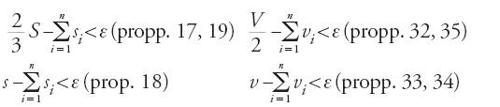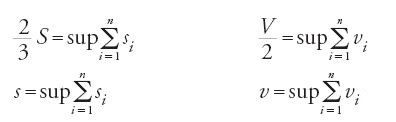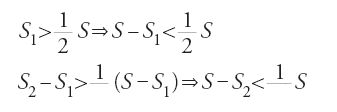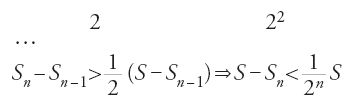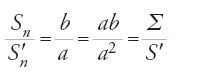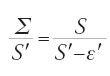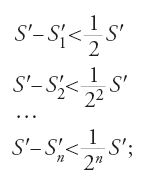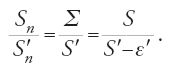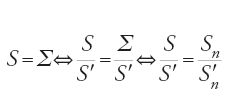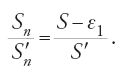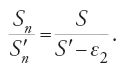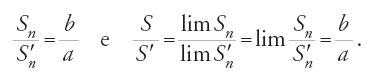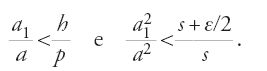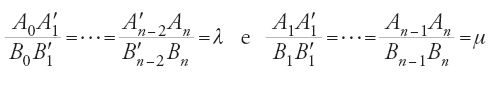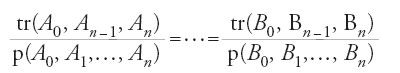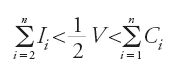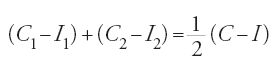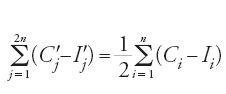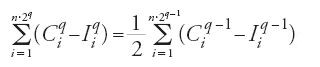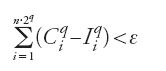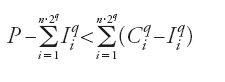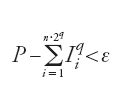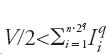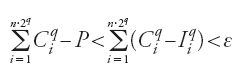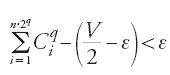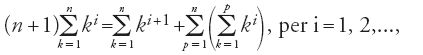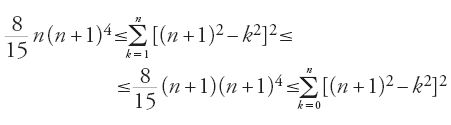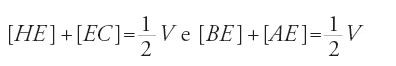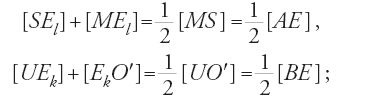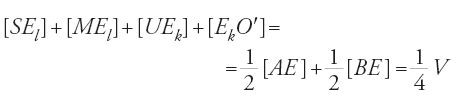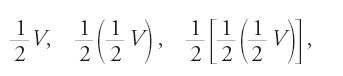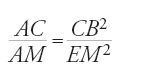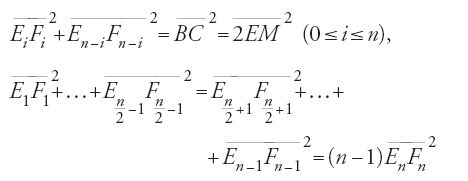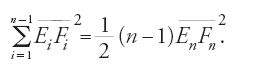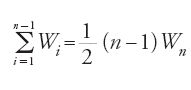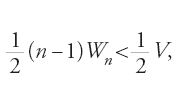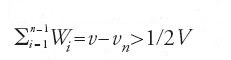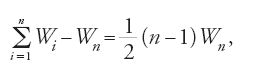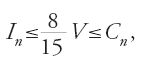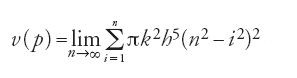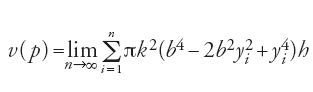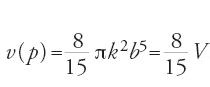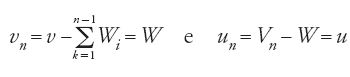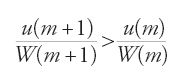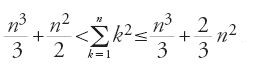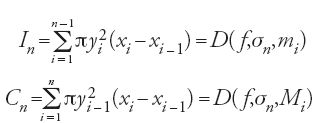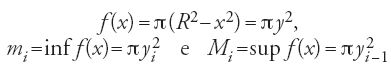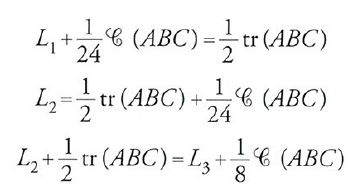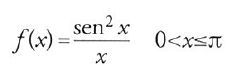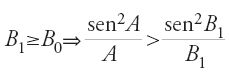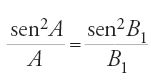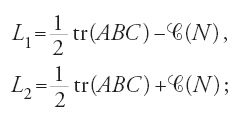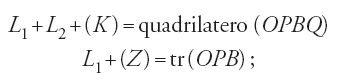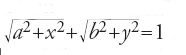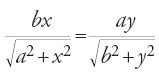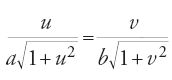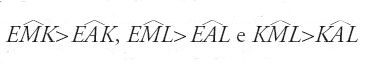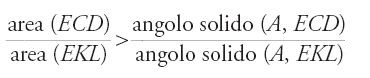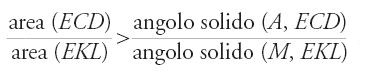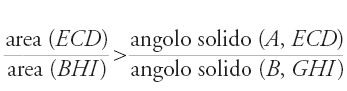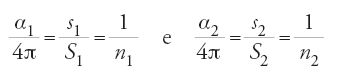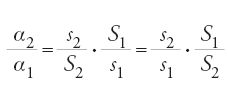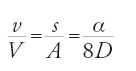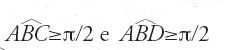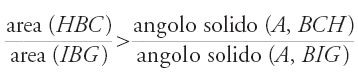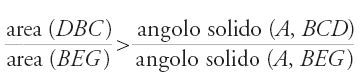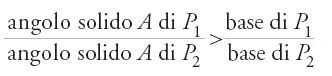La civiltà islamica: antiche e nuove tradizioni in matematica. Gli archimedei e i problemi infinitesimali

La civilta islamica: antiche e nuove tradizioni in matematica. Gli archimedei e i problemi infinitesimali

Gli archimedei e i problemi infinitesimali

La storia della geometria infinitesimale, e specialmente della parte che tratta di aree e volumi, delle superfici e dei solidi curvi, si caratterizza per un aspetto particolare. Dopo aver raggiunto i vertici che sappiamo negli scritti di Archimede, la ricerca si arresta di colpo per più di un millennio, per riprendere nel IX sec. con i matematici arabi. Nel corso di due secoli raggiungerà altre vette grazie a questi ultimi, prima di arrestarsi un'altra volta e in modo non meno deciso di come avvenne nel III sec. a.C. Si avrà una nuova rinascita nel XVII sec., e questa volta la ricerca non si fermerà più. Si tratta di un fenomeno storico che non è stato sufficientemente sottolineato, ma che merita di essere analizzato in modo da chiarire le ragioni per le quali la ricerca ha conosciuto questi due inizi e queste due interruzioni.

Un'anomalia non viene però mai sola. Anche l'impatto degli scritti di Archimede in questo campo si presenta, a partire dal IX sec., sotto una luce un po' paradossale. Pochissimo era noto in arabo di questi scritti, due trattati in tutto: La misura del cerchio e Della sfera e del cilindro. Tuttavia, malgrado il piccolo numero di testi tradotti, si avviano rapidamente a una ricerca molteplice e di alto livello. Per ragioni da attribuire al modo in cui il Corpus archimedeo è stato conservato e trasmesso, solamente un modesto numero di testi di Archimede era noto nella Tarda Antichità. Nel VI sec. Eutocio sembra conoscesse solo i due che abbiamo ora citato, e la situazione nella scienza araba era identica. Tutto sta a indicare che i traduttori non avevano a disposizione il Corpus archimedeo per intero, come invece accadeva per le opere di Euclide o di Apollonio. Possiamo anzi affermare senza tema di smentita che dei lavori di Archimede di matematica infinitesimale i matematici arabi conoscevano solo i due testi citati. Una conclusione stabilita a partire dall'esame dei loro lavori, e confermata dal matematico del XII sec. Ibn al-Sarī. Essi non conoscevano le opere La quadratura della parabola, Conoidi e sferoidi, Spirali, Il metodo, né direttamente né indirettamente. Questo fatto è importante perché il metodo archimedeo delle somme integrali che completava il metodo di esaustione si trova applicato solo nei Conoidi e sferoidi e nelle Spirali, cioè in trattati che i matematici arabi non conoscevano. Nemmeno i metodi archimedei per determinare l'area di un settore di parabola o il volume di un settore di paraboloide erano noti a questi matematici.

La questione si riduce quindi a scoprire come questi due trattati siano stati recepiti nella cultura araba, e ciò avrà la sua importanza nell'individuare gli aspetti che caratterizzano i matematici arabi appartenenti alla tradizione archimedea. Intanto, coloro che li hanno ricevuti e studiati erano impegnati in ricerche sulle sezioni coniche; qualche tempo dopo, a partire almeno dai Banū Mūsā, essi avranno a di sposizione le Coniche di Apollonio. Questi matematici si interessavano anche a discipline che qualcuno oggi chiamerebbe 'applicate': astronomia, statica, meccanica e ottica. Da questo interesse nasce lo sviluppo della ricerca sulle Coniche, le loro proprietà ottiche, il tracciato per punti mediante una trasformazione geometrica, il tracciato continuo mediante strumenti costruiti all'uopo, e ricerche sui metodi proiettivi. Ci aspettiamo quindi da parte loro l'introduzione di altri metodi oltre a quelli di Archimede, o il rafforzamento di procedimenti utilizzati da quest'ultimo ma in modo frammentario. E infatti questi matematici, impegnati nello studio delle trasformazioni puntuali e delle proiezioni, uniranno a tali metodi tecniche infinitesimali. Erano inoltre al corrente dei lavori dei colleghi algebristi, e ciò in qualche modo influenzerà le loro ricerche di geometria infinitesimale. Siamo in presenza di un insieme di conoscenze che daranno un'impronta ai concetti e metodi degli autori arabi della tradizione archimedea e determineranno lo sviluppo delle ricerche di geometria infinitesimale. Ci aspettiamo allora di vederli non soltanto approfondire la comprensione dei comportamenti asintotici e degli oggetti infinitesimali, ma anche estendere il campo di ricerca e includere altri settori della geometria infinitesimale non esplicitamente trattati dal matematico siracusano: problemi isoperimetrici nel piano e nello spazio, angolo solido, lunule. Si capisce quindi che questi archimedei non sono, come Eutocio, commentatori di Archimede, ma suoi emuli. D'altronde il numero dei commenti e delle redazioni in arabo dei due trattati di Archimede di geometria infinitesimale è estremamente ridotto: per quanto ne sappiamo, vi sono soltanto quelli di al-Kindī de La misura del cerchio, di al-Māhānī dell'opera Della sfera e del cilindro, e di Naṣīr al-Dīn al-Ṭūsī di entrambi questi trattati. Consideriamo ora brevemente e in modo sistematico i vari settori di questa geometria infinitesimale nella matematica dell'epoca dell'Islam classico.

Calcolo delle aree e dei volumi infinitesimali

I fondatori

Il primo testo arabo che si conosce sui problemi archimedei è un commento del filosofo e matematico al-Kindī alla terza proposizione (approssimazione di π) de La misura del cerchio, intitolato Risālat al-Kindī ilā Yūḥannā ibn Māsawayh fī taqrīb al-dawr min al-watar (Epistola di al-Kindī a Yūḥannā ibn Māsawayh sull'approssimazione del rapporto della circonferenza al diametro) e redatto prima del l'856. Già in questo lavoro si può constatare l'impatto dell'algebra. Al-Kindī ricorre infatti al vocabolario algebrico per certi termini e per esprimere rapporti tra numeri e segmenti, rapporti quindi che nessun greco antico avrebbe ammesso. Questo suo commento sarà noto anche in lingua latina, come sembrano attestare le celebri 'Versioni di Firenze'. Il vero rinnovamento della ricerca sui problemi archimedei comincia con tre contemporanei di al-Kindī, i fratelli Muḥammad, Aḥmad e al-Ḥasan, tutti noti con il nome di Banū Mūsā. Sono loro infatti a scrivere il celebre Kitāb Ma῾rifat misāḥat al-aškāl al-basīṭa wa-'l-kuriyya (Libro per conoscere l'area delle figure piane e sferiche), la prima opera di archimedei arabi. Soffermiamoci su questo libro, contemporaneo della ricezione dell'opera di Archimede.

Basta un semplice sguardo per capire che si tratta effettivamente di un libro che si inscrive nella tradizione archimedea, ma senza per questo prendere a modello Della sfera e del cilindro. Anzi, gli autori non seguono affatto l'approccio di Archimede, anche se certe idee fondamentali restano le stesse. In questo trattato di diciotto proposizioni essi affrontano quattro temi: la misura del cerchio, quella della superficie della sfera e il volume di questa, la formula di Erone di Alessandria per l'area del triangolo e, infine, la questione delle due medie proporzionali e la trisezione dell'angolo. Alla fine del trattato i Banū Mūsā danno un giudizio sul contributo da loro dato scrivendo: "Tutto ciò che abbiamo descritto nel nostro libro è opera nostra, eccetto la conoscenza della circonferenza a partire dal diametro, che è dovuta ad Archimede, e la conoscenza della posizione di due grandezze tra altre due grandezze affinché [tutte e quattro] si susseguano secondo uno stesso rapporto, che si deve a Menelao, come abbiamo ricordato prima" (Rashed 1996a, p. 132).

Questa dichiarazione, che passa di solito inosservata, merita invece una riflessione. Riprendiamo dunque brevemente lo studio dei Banū Mūsā per capire il senso di quanto essi dichiarano e allo stesso tempo quale sia precisamente la loro posizione nella tradizione archimedea. Cominciano col dimostrare la seguente proposizione: dato un cerchio di circonferenza p e un segmento di lunghezza l, sono possibili due casi: se l⟨p, si può inscrivere nel cerchio un poligono di n lati di perimetro p_n tale che l⟨p_n⟨p; se l>p si può circoscrivere al cerchio un poligono di n lati di perimetro q_n tale che p⟨q_n⟨l. La dimostrazione dei due casi poggia sull'esistenza di un cerchio di circonferenza data p e di un poligono regolare. Gli autori suppongono che un tale cerchio esista; e per il poligono ricorrono alla prop. 16 del Libro XII degli Elementi di Euclide: "Dati due cerchi che abbiano lo stesso centro, inscrivere nel cerchio maggiore un poligono equilatero, avente numero pari di lati, che non tocchi il cerchio minore". Si osservi che affinché un poligono regolare di n lati risponda al problema è necessario e sufficiente che il suo apotema a_n soddisfi:

dove r1 e r2 sono i raggi dei due cerchi concentrici, p1 e p2 le rispettive circonferenze (l'esistenza dell'intero n dipende dalla continuità della funzione coseno). Tuttavia, contrariamente a quanto si è potuto affermare, il ricorso alla proposizione citata degli Elementi non basta per stabilire la proposizione dei Banū Mūsā; occorre completarla con un'omotetia, una tecnica che al-Ḥasan ibn Mūsā conosceva.

Nella successiva proposizione i Banū Mūsā dimostrano per assurdo l'espressione dell'area del cerchio come prodotto del semidiametro per la semicirconferenza, ossia S=rp/2. Si osservi che per ottenere una contraddizione essi non confrontano S con S′>S, né S con S″⟨S, ma solo p con p′⟨p e p con p″>p, confrontano cioè le lunghezze.

Dopo aver così determinato l'area del cerchio si occupano dell'approssimazione di π con il metodo di Archimede, come essi stessi affermano, ma con qualche leggera modifica. È evidente che l'impostazione dei Banū Mūsā che abbiamo indicato è diversa da quella di Archimede in vari punti. La prima differenza riguarda proprio l'applicazione del metodo di esaustione e di quello, a esso complementare, della riduzione all'assurdo. Si è visto come, contrariamente ad Archimede, i Banū Mūsā aggirino il punto più delicato del metodo di esaustione, cioè il passaggio al limite (per usare il nostro linguaggio), ricorrendo alla prop. 16 del Libro XII degli Elementi, più un'omotetia, proposizione la cui dimostrazione si ottiene appunto passando al limite. Quanto alla riduzione all'assurdo abbiamo visto che essi confrontano lunghezze, e non aree come faceva Archimede. Infine, essi non determinano l'area del cerchio per confronto con un'altra figura, quella del triangolo rettangolo nel quale un cateto è uguale al raggio e l'altro alla circonferenza, ma direttamente, come prodotto di due grandezze. In queste condizioni si comprende come la loro dimostrazione sia più breve di quella di Archimede.

Resta da scoprire se la strada seguita dai Banū Mūsā sia stata presa volutamente, o sia dovuta alle circostanze. Per rispondere occorre avere un'idea dello studio da loro compiuto sul secondo tema, la misura della superficie e del volume della sfera. Cominciano dimostrando la proposizione seguente (prop. 11). L'area laterale di un tronco di cono di rivoluzione a basi parallele è data da: S=l(p1+p2)/2, dove l è la lunghezza della generatrice, p1 e p2 i perimetri delle due basi. La prop. 12 afferma che, se si divide il quarto di cerchio A1B in n archi uguali mediante i punti A2, A3,…, A_n, allora:

Eseguiti i calcoli, [2] e [3] si riscrivono come

,

relazioni soddisfatte per ogni n. Nella prop. 13 considerano un semicerchio nel quale viene inscritta una linea poligonale regolare con un numero pari di lati. Tracciano poi in questa il semicerchio inscritto. Per rotazione sono generati una semisfera e un solido di rivoluzione di area laterale S formato da un cono e da vari tronchi di cono, assieme a un'altra semisfera inscritta nel solido di rivoluzione e che ha lo stesso centro della prima. I Banū Mūsā dimostrano che 2πR21⟨S⟨2πR22, dove R1 e R2 sono rispettivamente i raggi del cerchio inscritto e del cerchio circoscritto. Osserviamo che le ipotesi sono quelle della prop. 12, e che la dimostrazione utilizza le propp. 11 e 12, senza far uso della prop. 16 del Libro XII degli Elementi. Possono ora applicare la riduzione all'assurdo due volte, la prima nella prop. 14 per ottenere l'area laterale di una semisfera, il doppio di quella di un cerchio massimo, come essi dicono, e cioè S=2πR2; la seconda per dedurre il volume della sfera come prodotto del semidiametro per un terzo della superficie, cioè (4/3)πR3.

Ritroviamo anche qui le differenze tra Archimede e i Banū Mūsā constatate nel caso della misura del cerchio. La prima riguarda ancora il metodo di esaustione. I Banū Mūsā applicano anche questa volta la prop. 16 del Libro XII degli Elementi, assieme a un'omotetia, e non la prop. 17 dello stesso libro come si è creduto. Considerano infatti un solido inscritto nella semisfera formato da coni e tronchi di cono, solido la cui superficie è esterna a quella di una semisfera concentrica alla prima e contenuta in questa. Un tale solido si ottiene da una poligonale regolare inscritta in un cerchio massimo della sfera e che non tocca il cerchio massimo della seconda sfera contenuto nel primo (si parte quindi sempre dalla citata prop. 16 di Euclide). Questo procedimento permette di evitare il passaggio al limite per le serie di seni già menzionate. D'altra parte, anche qui, quando si tratta di determinare il volume della sfera, la riduzione all'assurdo avviene per le superfici laterali e non per i volumi. Infine, il volume della sfera non viene dato, come invece in Archimede, in termini di un altro volume (un cono avente base equivalente a un cerchio massimo della sfera e altezza uguale al raggio), ma come prodotto di due grandezze.

Questo studio dei Banū Mūsā ebbe effetti importanti, anche se di diversa natura, sulla matematica. Per prima cosa, nel mondo arabo, questa tappa iniziale ‒ che sarà superata rapidamente ‒ ebbe un certo impatto sulla ricerca, ma soprattutto sull'insegnamento. A cominciare dal loro collaboratore Ṯābit ibn Qurra, e per un secolo e mezzo, si proseguirà lo studio della misura delle superfici e dei volumi curvi. Questa tradizione riscopre il metodo delle somme integrali, pur sviluppando i metodi geometrici che permettono di facilitare l'applicazione del metodo di esaustione, come per esempio l'affinità. La misura della sfera sarà ripresa più tardi da Ibn al-Hayṯam, utilizzando però le somme di Darboux. Nella tradizione araba il trattato dei Banū Mūsā sopravviverà soprattutto come libro per l'insegnamento, come dimostra il gran numero di copie trovate nelle raccolte di manoscritti ed evidentemente destinate a questo scopo. In latino la situazione è del tutto diversa. Tradotto da Gherardo da Cremona il trattato costituisce, assieme a La misura del cerchio di Archimede (tradotto in latino dalla versione araba), l'opera di riferimento principale nella ricerca matematica archimedea. A questo trattato si sono interessati, tra molti altri, Fibonacci, Giordano Nemorario, l'autore ignoto del Liber de triangulis e Ruggero Bacone.

Abbiamo rilevato come i commentatori più moderni di questo trattato, in lavori peraltro eccellenti, si siano ingannati pensando che i Banū Mūsā avessero fatto ricorso alla sola prop. 16 del Libro XII di Euclide, e soprattutto affermando che essi utilizzavano la successiva prop. 17. Una disattenzione dovuta al mancato riconoscimento dell'uso peraltro esplicito delle trasformazioni geometriche (dell'omotetia), in quanto il contributo dei Banū Mūsā è stato esaminato alla luce della vecchia geometria. Basta invece scorrere il libro di al-Ḥasan ibn Mūsā sull'ellisse, intitolato Kitāb al-šakl al-mudawwar al-mustaṭīl (Libro sulla figura circolare allungata), per capire l'importanza crescente che assume in geometria lo studio delle trasformazioni geometriche. È proprio in questo che la geometria degli Arabi si allontanerà sempre più dalle proprie origini greche ed ellenistiche. È una tesi che per noi è fondamentale, e che impone, tra l'altro, di riscrivere la storia della geometria dell'epoca. Per sottolineare soltanto ciò che qui ci interessa, fin dall'inizio si osserva che la tradizione archimedea in arabo, per sviluppare una geometria infinitesimale, tende a indirizzare la ricerca in geometria verso lo studio delle trasformazioni puntuali. La storia di questa tradizione appare allora sotto una luce diversa, e la posizione dei Banū Mūsā si modifica. Veniamo allora a questo secondo libro, necessario secondo noi per la comprensione del primo.

Al-Ḥasan ibn Mūsā si propone di determinare l'area dell'ellisse e delle sezioni ellittiche. Sappiamo che ancora non disponeva di una versione comprensibile delle Coniche di Apollonio. Le sue ricerche miravano anche a sviluppare lo studio delle sezioni coniche a partire dalle sezioni piane del cilindro. È solo dopo la sua morte che il fratello Aḥmad ibn Mūsā trova l'edizione di Eutocio dei primi quattro libri delle Coniche, ciò che rendeva possibile la traduzione araba dell'insieme dei sette libri dell'opera di Apollonio, l'ottavo essendo già andato perduto in greco. In altri termini, al-Ḥasan ibn Mūsā cerca di raggiungere due scopi: uno, per così dire archimedeo, riguarda la misura di un'area limitata da una curva; l'altro, nella tradizione di Apollonio (anche se non poteva conoscere a fondo le Coniche), riguarda lo studio delle proprietà geometriche delle curve. Egli unisce le nozioni di proiezione e di affinità ortogonale all'applicazione della prop. 2 del Libro XII degli Elementi e alla riduzione all'assurdo: è il primo cambiamento di direzione della matematica archimedea. Seguiamo brevemente il suo procedimento.

Secondo il libro di Ibn al-Samḥ, che riassume il trattato di al-Ḥasan ibn Mūsā, il procedimento di quest'ultimo si articola come segue: egli prende l'avvio dalla 'figura circolare allungata' definita dalla proprietà bifocale MF+MF′=2a, dove 2a è l'asse maggiore, per stabilire poi che la sezione piana di un cilindro di rivoluzione con un piano non parallelo alle basi, cioè un'ellisse, ha le stesse proprietà della prima figura. Determina in seguito l'asse dell'ellisse per studiare infine le proprietà delle corde, delle frecce e così via. Lo schema del suo ragionamento deduttivo mostra che le prime sei proposizioni riguardano la figura circolare allungata, i suoi vertici, il centro, i diametri, le corde, l'asse, il cerchio inscritto che ha per diametro l'asse minore e il cerchio circoscritto che ha per diametro l'asse maggiore. Le cinque proposizioni successive riguardano l'ellisse come sezione piana, e l'identificazione di questa con la curva precedente. Segue un gruppo di otto proposizioni che trattano della misura dell'area dell'ellisse. Consideriamo in sintesi questi gruppi.

Nella penultima proposizione del primo gruppo (prop. 5) si legge: se si associa a un punto M della figura circolare allungata il punto T del cerchio inscritto che ha la stessa ordinata (MT è ortogonale a BD nel punto K), si ha: MK2=KT2+(OA−MF)2 che, nel sistema di coordinate x=MK, y=MH, posto AC=2a, BD=2b, FF′=2c, KT=X, e MF=a−(cx/a) (relazione stabilita in precedenza), si riscrive come

(se si divide per b2 si ritrova l'equazione dell'ellisse). La prop. 6 riguarda l'affinità ortogonale relativa all'asse minore:

dalla [6] si ha:

,

da cui si ottiene

,

affinità ortogonale di asse BD, rapporto a/b>1, nella quale la figura circolare allungata ABCD è l'immagine del cerchio di diametro BD (questa affinità è una dilatazione).

Nel secondo gruppo di proposizioni, dedicate all'ellisse come sezione piana del cilindro retto, al-Ḥasan ibn Mūsā, dopo aver ricordato la proprietà secondo la quale la sezione di un cilindro retto a base circolare con un piano che taglia l'asse e non è parallelo alla base è un'ellisse con centro sull'asse, considera una famiglia di curve che si deformano con continuità dal cerchio all'ellisse. Studia poi l'affinità ortogonale relativa all'asse minore (prop. 7): sia data un'ellisse ADBG e un cerchio inscritto EDZG, se una parallela ad AB taglia GD in H, il cerchio in K e l'ellisse in T, allora:

Nel corso della dimostrazione egli considera l'ellisse ADBG come il ribaltamento dell'ellisse DLG che si ottiene facendo ruotare ADBG intorno a DG sul piano perpendicolare in N all'asse del cilindro. Il cerchio DEG è la proiezione cilindrica dell'ellisse DLG su questo stesso piano.

Nella prop. 8 egli studia l'affinità ortogonale relativa all'asse maggiore. L'ellisse si considera in questo caso come l'immagine del cerchio circoscritto in un'affinità ortogonale di rapporto b/a (una contrazione). In altri termini, e in un linguaggio analitico che al-Ḥasan ibn Mūsā non conosceva, se in un riferimento ortogonale si considerano l'ellisse E e i cerchi C1 e C2 tali che (a>b):

e se ψ e φ denotano la dilatazione e la contrazione già viste, allora

Formula 12a e 12b

A questo punto egli dimostra che le due figure, cerchio allungato ed ellisse, sono sovrapponibili punto per punto (prop. 9). Sono questi i mezzi concettuali che egli utilizzerà in seguito per determinare l'area dell'ellisse. Innanzitutto mostra mediante una dilatazione che il rapporto tra l'area di un poligono inscritto nell'ellisse e quella di un poligono inscritto nel cerchio inscritto nell'ellisse è uguale al rapporto tra asse maggiore e asse minore. Precisa poi questi risultati per ottenere πab come area dell'ellisse.

Questo è in breve il procedimento di al-Ḥasan ibn Mūsā, un percorso che getta luce sia sul libro dei Banū Mūsā prima considerato, sia sui risultati dei matematici archimedei loro eredi. L'uso di un'omotetia nel libro dei Banū Mūsā è del tutto naturale; il ricorso alle trasformazioni puntuali da parte dei loro successori, come Ṯābit ibn Qurra, il nipote Ibrāhīm ibn Sinān e molti altri, ha origine nei Banū Mūsā stessi. La fisionomia di questi ultimi ne esce trasformata. Non si tratta più della pallida immagine dei commentatori di Archimede, bensì di matematici che per iniziare una nuova tradizione cominciano con il rivedere la vecchia. I loro eredi, matematici di genio, andranno presto più lontano, gettando così, paradossalmente, un velo sulla loro importanza e sul loro ruolo. Gli storici della matematica se la sono cavata attribuendo ai loro successori, e in particolare a Ṯābit ibn Qurra, alcune delle loro invenzioni, mescolando due aspetti che sono invece ben distinti: quello trasmesso dalla matematica latina e quello che si ritrova nella matematica araba.

Come abbiamo visto, nel momento stesso in cui si traducevano due testi di Archimede, i matematici del IX sec. cercavano strade loro proprie per raggiungere gli stessi risultati, o altri e nuovi. Questa ricerca di nuove strade non si limita nei Banū Mūsā e nei loro successori all'insegnamento archimedeo, ma compare anche nei lavori di meccanica e di astronomia. Anzi, la stessa tendenza si può osservare anche nelle altre discipline matematiche: aritmetica, teoria dei numeri, algebra, trigonometria, metodi proiettivi, ecc., e in altre discipline scientifiche come l'ottica con al-Kindī e la statica con Ṯābit ibn Qurra. Questo nuovo spirito scientifico che si forma nel IX sec., nella tradizione della scienza ellenistica ma con una grande libertà nei confronti di quest'ultima, libertà di inventare, criticare, e attingere ad altre fonti ‒ fonti indiane per esempio ‒, spiega almeno in parte un fenomeno che continua a sorprendere: la traduzione massiccia, ripetuta più volte e sempre più veloce dell'eredità antica.

I contemporanei e gli eredi dei Banū Mūsā proseguiranno molto attivamente le ricerche in questo campo. Un loro collaboratore, Ṯābit ibn Qurra (826-901), darà un contributo molto consistente. Scriverà tre trattati, uno dedicato all'area di un settore parabolico, un secondo al volume di un paraboloide di rivoluzione e il terzo alle sezioni e all'area laterale del cilindro. Questi lavori saranno nuovi punti di partenza per altri matematici, che si occupano di ridurre il numero dei lemmi e di migliorare i metodi. La misura della parabola sarà ripresa per esempio da al-Māhānī, da Ibrāhīm ibn Sinān e da Ibn Sahl, quella del paraboloide da al-Qūhī e poi da Ibn al-Hayṯam. Tutto ciò mostra il ruolo, che si può definire fondatore, svolto dagli scritti di Ṯābit ibn Qurra per questo argomento, come per molti altri.

Nel primo trattato, Kitāb fī misāḥat qiṭ῾ al-maḫrūṭ allaḏī yusammā al-mukāfi᾽ (Libro sulla misura della sezione di un cono detta parabola), nel quale si propone di determinare l'area di un settore parabolico, Ṯābit ibn Qurra, che non conosceva lo studio di Archimede in proposito, dimostra ventuno risultati. I primi riguardano la somma di varie progressioni aritmetiche; dimostra per esempio che:

Dopo undici lemmi aritmetici egli enuncia quattro lemmi riguardanti le successioni di segmenti, successioni che gli servono per studiare la maggiorazione. Nel lemma 14 dimostra che: se a e b sono due segmenti dei quali si conosce il rapporto a/b, allora esiste un intero positivo n tale che la successione (u_k)1≤_k≤_n degli n numeri dispari successivi a partire da 1 e la successione (v_k)1≤_k≤_n dei numeri pari successivi a partire da 2 soddisfano la seguente relazione:

Con questo risultato egli introduce l'appros simazione che utilizzerà nel lemma successivo per ottenere la suddivisione dei segmenti. Tale lemma si enuncia così: siano AB e H due segmenti, a e b due segmenti di rapporto a/b dato. Per n qualunque si ha: (a) esiste una partizione (A_k)0≤_k≤_n, k=0, 1,…, n, con A0=A, A_n=B e tale che

,

dove (u_k)1≤_k≤_n, k=1, 2,…, n, è la successione dei numeri dispari a partire da 1; (b) esiste una successione di segmenti (H_j)1≤_j≤_n, j=1, 2,…, n, con H_n=H e tale che

,

con (v_j)1≤_j≤_n, j=1, 2,…, n, la successione dei numeri pari a partire da 2. Se n soddisfa la [14] allora

La dimostrazione poggia sulla suddivisione di un dato segmento in una successione di segmenti proporzionali ai numeri di una successione data e sulla generalizzazione del lemma 14 che introduce l'approssimazione a delle successioni di segmenti, e dunque sulla generalizzazione della maggiorazione di una successione di rapporti di segmenti.

Dopo i quindici lemmi, undici dei quali aritmetici e quattro relativi alle successioni di segmenti, Ṯābit ibn Qurra affronta il calcolo dell'area di un settore parabolico. A questo scopo dimostra quattro proposizioni. L'esame dei lemmi e di queste proposizioni prova che aveva una conoscenza precisa e rigorosa della nozione di estremo superiore di una successione di quadrati di numeri reali e della sua unicità. Per caratterizzare l'estremo superiore fa uso della seguente proprietà.

Sia BAC un settore parabolico di diametro AD, sia S l'area del parallelogramma di base BC associato alla parabola. Al lora per ogni ε>0 esiste una suddivisione A, G1, G2, …, G_n−1, D del diametro AD tale che la differenza fra l'area di BAC e l'area del poligono BE_n−1…E2_E1AF1F2…F_n−1C è minore di ε. Egli dimostra in modo rigoroso che l'estremo superiore delle aree dei poligoni ottenuti è 2/3 dell'area di BHMC, e perviene infine al teorema seguente: l'area della parabola è infinita, ma l'area di un qualunque settore è uguale a 2/3 dell'area del parallelogramma associato al settore.

Sia S l'area del settore parabolico P, e S l'area del parallelogramma a esso associato. Se (2/3)S S si hanno due casi. Nel primo caso, S>(2/3)S.

Sia ε>0 tale che

Per la prop. 18, per questo ε esiste N tale che, per n>N, il poligono P_n di area S_n soddisfa la relazione:

Da [18] e [19] si ha [(2/3)S+ε]−S_n⟨ε, da cui: (2/3)S⟨S_n. Ma per la prop. 17 si ha (2/3)S>S_n, da cui la contraddizione. Nel secondo caso, S⟨(2/3)S. Sia ora ε>0 tale che

Per la prop. 19, per questo ε esiste N tale che, per n>N, il poligono P_n di area S_n soddisfa la relazione:

per [20] e [21] si ha (S+ε)−S_n⟨ε, da cui S⟨S_n. Ma P_n è inscritto in P, e dunque S_n⟨S. Di qui la contraddizione. Si ha quindi (2/3)S=S.

Questo teorema equivale a dimostrare l'unicità dell'estremo superiore e utilizza nella dimostrazione essenzialmente le proprietà dell'estremo superiore. Infatti, si vuole dimostrare che (2/3)S=S, sapendo che

Per riduzione all'assurdo, si suppone S (2/3)S. Vi sono due ca si. Nel primo, se S>(2/3)S, allora esiste ε>0 tale che S−(2/3)S=ε. Ma per [22] S è il più piccolo maggiorante degli S_n, e dunque per questo ε esiste S_n tale che S_n>S−ε, e dunque (2/3)S⟨S_n; assurdo, in quanto per [23], (2/3)S è un maggiorante degli S_n. Nel secondocaso, S⟨ (2/3)S, dunque esiste ε>0 tale che (2/3)S−S=ε. Ma per [23], (2/3)S è il più piccolo maggiorante degli S_n tale che S_n>(2/3)S−ε, e dunque S⟨S_n; assurdo poiché per [22] S è un maggiorante degli S_n.

Non pretendiamo di affermare con questo che Ṯābit ibn Qurra, non più dei suoi predecessori né dei suoi successori fino al XVIII sec., abbia definito il concetto di estremo superiore. In compenso ci sembra che egli utilizzi le proprietà dell'estremo superiore come idea guida nella misura degli insiemi convessi. Nel procedimento di Ibn Qurra si può in realtà riconoscere l'idea fondamentale che è alla base dell'integrale di Riemann. Infatti, nel caso particolare in cui il diametro considerato è l'asse della parabola, il procedimento equivale a considerare una suddivisione σ=AG1G2…G_n−1 del diametro AD, prendere la somma

e dimostrare che, per ogni ε>0, esiste un σ tale che la differenza fra l'area ACD e Sσ è minore di ε, e dimostrare infine che Sσ converge a quest'area.

Traduciamo quanto precede nel linguaggio dell'analisi: sia x_i l'ascissa di G_i e sia y=f(x) l'equazione della parabola. Sσ si può allora scrivere:

ma poiché

e poiché f è continua, si deduce che

è un valore che f assume nel punto ξ_i dell'intervallo [x_i−1,x_i].

Ma Sσ si può allora scrivere nella forma:

,

cioè nient'altro che la somma utilizzata nella definizione dell'integrale di Riemann di una funzione f. Osserviamo infine che la quadratura di Ibn Qurra, data la definizione della parabola, è equivalente al calcolo dell'integrale ∫^a₀ √px dx. Ecco quanto scrive uno storico moderno, Adolf P. Youschkevitch:

Grazie a questo procedimento, Ibn Qurra fa rivivere il metodo, caduto nell'oblio, del calcolo delle somme integrali. Inoltre, con questo stesso procedimento, Ibn Qurra calcola effettivamente per la prima volta un integrale ∫^a₀ xⁿ dx per un valore frazionario dell'esponente n, qui ∫^a₀ x^1/2 dx.

Così facendo, sempre per la prima volta, suddivide l'intervallo d'integrazione in parti disuguali. Con un procedimento analogo, che consiste nel suddividere l'asse delle ascisse in segmenti che costituiscono una serie geometrica, Pierre Fermat, alla metà del XVII secolo, affronterà la quadratura delle curve y=x^m/n con (m,n)≠1. (1976, p. 43)

Dopo aver calcolato l'area della parabola, Ṯābit ibn Qurra affronta il calcolo del volume di un paraboloide di rivoluzione nella sua Maqāla fī misāḥat al-muǧassamāt al-mukāfi᾽a (Trattato sulla misura dei paraboloidi). Si tratta di passare dal piano allo spazio, e a questo scopo egli stabilisce trentasei proposizioni suddivise in vari gruppi. Dimostra infine il teorema seguente: il volume v di una cupola parabolica ABC di asse BD è la metà del volume V del cilindro di altezza h e cerchio di base di diametro AC:

Il procedimento è dunque analogo a quello seguito per determinare il settore parabolico. Utilizza una suddivisione del diametro di un settore parabolico in segmenti proporzionali alla successione dei numeri dispari. I punti della parabola associata a questa suddivisione hanno allora ascisse proporzionali ai quadrati degli interi e ordinate proporzionali alla successione degli interi. Questi punti determinano:

Egli dimostra che, dato ε>0, si può trovare un N tale che, per ogni n>N, si abbia:

In altri termini, egli dimostra che:

Con un ragionamento per assurdo dimostra poi in entram bi i casi l'unicità dell'estremo superiore:

Il contributo di Ibn Qurra in questo campo non si ferma qui. Egli scriverà un libro fondamentale, Kitāb fī quṭū῾ al-usṭuwāna wa-basīṭi-hā (Libro sulle sezioni del cilindro e sulla sua superficie laterale), nel quale si studiano le diverse sezioni piane di un cilindro retto e di un cilindro obliquo, si determina l'area dell'ellisse e dei settori ellittici, si discutono le sezioni massimali e minimali del cilindro e i loro assi, e viene infine determinata l'area della parte della superficie delimitata da due sezioni piane. Come i due precedenti, questo trattato non solo ha lasciato il segno nella storia della geometria infinitesimale, ma è anche uno dei testi più importanti di tutta la geometria. Infatti, affrontando lo studio delle trasformazioni geometriche puntuali, esso indirizza la ricerca geometrica in una direzione nuova, e in questo modo feconderà l'algebra. Se ne troveranno le tracce nelle opere, tra gli altri, di Ibrāhīm ibn Sinān, di Ibn Sahl, di al-Qūhī, di Ibn al-Hayṯam e di Šaraf al-Dīn al-Ṭūsī.

È impossibile riportare qui tutti i risultati e le dimostrazioni di questo trattato ricco e profondo. Ci limitiamo per fissare le idee, a due proposizioni. Nella prop. 14 Ṯābit dimostra che, se S è l'area dell'ellisse E di assi 2a e 2b e Σ quella del cerchio E di raggio r=√ab, allora S=Σ. Si presenta di seguito la traduzione in simboli della sua dimostrazione, con le notazioni seguenti: S area dell'ellisse E; S_n area di P_n inscritto in E; Σ area del cerchio equivalente E; Σ_n area di Π_n inscritto in E; S′ area del cerchio circoscritto C; S′_n area di P′_n inscritto in C. Supponiamo che S Σ. Si hanno allora due casi. Nel primo caso, se S>Σ, allora S=Σ+ε. Sia P_n un poligono di 2ⁿ+1 lati inscritto nell'ellisse E e ottenuto da P_n−1 raddoppiandone il numero dei vertici mediante tagli dell'ellisse con diametri che passano per i centri dei lati di P_n−1. P1 è il rombo definito dai vertici dell'ellisse. Se S_n è l'area di P_n, si ha successivamente:

Formula 33a e 33b

allora, per ε dato da S=Σ+ε esiste un intero positivo n tale che (1/2ⁿ)S⟨ε, da cui S−S_n⟨ε e S_n>Σ. Si considera allora il cerchio C e il poligono P′_n ottenuti da E e da P_n per affinità ortogonale di rapporto a/b. Sia S′_n l'area di P′_n e S′ l'area di C; si ha:

ma S_n>Σ, da cui S′_n>S′, ciò che è impossibile.

Nel secondo caso, se S⟨Σ, si ha S/S′⟨Σ/S′, da cui

Riprendendo il cerchio C e i poligoni P′_n precedenti si ha successivamente

allora, per ε′ definito da [35] esiste un intero positivo n tale che (1/2ⁿ)S′⟨ε′, e dunque

Se P_n è il poligono inscritto in E corrispondente a P′_n nell'affinità ortogonale di rapporto b/a, allora:

ma per [37] si ha S′_n>S′−ε′, da cui S_n>S, il che è assurdo. Dopo l'esame dei due casi si ottiene quindi S=Σ.

Si passa dall'ellisse E al cerchio C con una dilatazione ortogonale f di rapporto k1=a/b e dal cerchio C di raggio a al cerchio E di raggio r tale che r2=ab con un'omotetia h di rapporto k₂=r/a=√ab/a=√b/a. Dunque, E=h°f(E); la trasformazione h°f conserva le aree, in quanto k1∙k22=1. Lo scopo della prop. 14 è precisamente quello di mostrare questa proprietà nel caso dell'ellisse E.

Con le notazioni precedenti, Ṯābit utilizza le uguaglianze Σ/S′=b/a=k22, e dimostra che S_n/S′_n=b/a=1/k1 per ogni n, da cui

Il suo metodo consta dunque dei due passi seguenti. Nel primo passo, per S_n/S′_n⟨S/S′, si ha

Si dimostra che esiste P_n⊂E tale che S−ε1⟨S_n⟨S; ma f(P_n)=P′_n⊂C soddisfa [40], da cui S′_n>S′, e ciò è impossibile. Nel secondo passo, per S_n/S′_n>S/S′, si ha

Si dimostra che esiste P′_n⊂C tale che S′−ε2⟨S′_n⟨S′; ma f−1(P′_n)=P_n⊂E soddisfa [41], da cui S_n>S, impossibile. Si è dunque dimostrato che

Dunque, a partire dalla proprietà dell'affinità ortogonale secondo la quale il rapporto delle aree S′_n e S_n dei due poligoni omologhi P_n e P′_n è uguale al rapporto a/b dell'affinità, qualunque sia n, Ṯābit deduce che lo stesso accade per l'area S dell'ellisse E e l'area S′ del cerchio C. Ciò equivale a dire che il rapporto si conserva per passaggio al limite: per ogni n intero positivo

Luca Valerio (1552-1618) prenderà affermazioni di questo tipo come base del suo metodo (De centro gravitatis solidorum libri tres, Libro II, propp. I-III), un metodo che non fa intervenire somme integrali.

Lo stesso risultato è contenuto nella prop. 4 dell'opera Conoidi e sferoidi di Archimede, un testo che però non era conosciuto dai matematici dell'epoca, nemmeno da Ṯābit. Il confronto tra il procedimento di Archimede e quello di Ṯābit è doppiamente istruttivo: potremo apprezzare di più il contributo del matematico del IX sec., e capire meglio quale fosse la conoscenza che si aveva in quell'epoca del Corpus archimedeo.

Nella prop. 31 Ṯābit dimostra che l'area laterale Σ di una porzione di cilindro obliquo compresa tra due sezioni rette è Σ=pl, se p è la lunghezza di un'ellisse minimale e l la lunghezza del segmento di generatrice tra le due sezioni. Sia E una delle sezioni, K il centro di questa, 2a l'asse maggiore. Distinguiamo di nuovo due casi. Nel primo caso, se Σ⟨pl, esiste g, con g⟨p, tale che Σ=gl. Sia h tale g⟨h⟨p; esiste un'area ε tale che Σ+ε=hl, da cui ε=l(h−g). Si costruisce l'ellisse E1=φ(E), dove φ è l'omotetia di centro K e di rapporto a1/a tale che 1>a1/a>h/p; per la prop. 26 la lunghezza p1 è tale che p1/p=a1/a, da cui p1/p>h/p, e dunque p1>h.

Sia P_n un poligono inscritto in E e che non tocca E1, P′_n la sua proiezione sull'altra base e p_n il perimetro. Se Σ_n è l'area laterale del prisma di basi P_n e P′_n si ha Σ_n=p_nl; ma p_n>p1>h, da cui Σ_n>hl, e dunque

a) Se ε/2≥s, poiché le aree s e s′ delle due basi che sono ellissi minimali sono uguali, si ha ε≥s+s′, da cui Σ_n>Σ+s+s′. L'area laterale del prisma inscritto nel cilindro sarebbe maggiore dell'area totale, il che è assurdo.

b) Se ε/2⟨s si impone inoltre ad a1 la condizione a12/a2>[s−(ε/2)]/s; ma se s1 è l'area di E1, s1/s=a12/a2, da cui s−s1⟨ε/2. Se s_n è l'area di P_n e s′_n quella di P′_n, si ha s_n=s′_n, s>s_n>s1, s−s_n⟨ε/2 e ε>(s−s_n)+(s′−s′_n). Dalla [44] si trae Σ_n>Σ+(s−s_n)+(s′−s′_n), assurdo. Per (a) e (b) si arriva a una contraddizione; pertanto Σ≥pl. Passiamo ora al secondo caso; se Σ>pl esiste g, con g>p, tale che Σ=gl. Siano h tale che p⟨h⟨g ed ε un'area tale che Σ=hl+ε. Sia E1=φ(E), dove φ è l'omotetia di centro K e rapporto a1/a tale che

Se p1 è la lunghezza di E1 si ha p1/p=a1/a, da cui p1⟨h. Si inscriva in E1 un poligono P_n senza punti in comune con E; con le notazioni della prima parte si ha Σ_n=p_nl; ma h>p1>p_n da cui Σ_n⟨hl, e dunque:

Tuttavia essendo s1/s=a21/a2 , allora s1⟨s+(ε/2); cioè s1−s>s_n−s, da cui s_n−s⟨ε/2. Per la convessità sappiamo che Σ_n+(s_n−s)+(s′_n−s′)>Σ, da cui Σ_n+ε>Σ, contro la [46]. Dopo l'esame dei due casi si conclude quindi che Σ=pl.

Osserviamo che le sole aree di superfici considerate fino ad allora erano quelle del cilindro retto, del cono retto e della sfera (Archimede, Della sfera e del cilindro). Ṯābit è il primo a studiare l'area del cilindro obliquo, che verrà espressa nella matematica moderna da un integrale ellittico (la lunghezza p dell'ellisse di base). Questa proposizione rappresenta una tappa verso la determinazione dell'area laterale di una porzione di cilindro obliquo compresa tra due piani, paralleli o no. È precisamente ciò che Ṯābit stabilisce nelle proposizioni successive.

Gli eredi

Con i contributi dei Banū Mūsā e di Ṯābit ibn Qurra la ricerca in geometria infinitesimale riposa su basi solide e ha fatto notevoli passi avanti. Questi matematici fornirono importanti esperienze, da cui ripartire per un nuovo inizio: comicia l'epoca degli eredi. Queste esperienze non si riducono ai teoremi dimostrati, sebbene essi siano numerosi, ma comprendono anche metodi nuovi e la riscoperta di quelli vecchi. Abbiamo assistito allo sviluppo di due tipi di metodi. Già con al-Ḥasan ibn Mūsā e i suoi fratelli Muḥammad e Aḥmad, e con Ṯābit ibn Qurra nel suo ultimo trattato, abbiamo visto manifestarsi i metodi basati su trasformazioni geometriche. Abbiamo visto d'altra parte che Ṯābit ibn Qurra reintroduce il concetto di somma integrale, certamente già presente in Archimede ma non nei trattati tradotti in arabo. Lo studio approfondito dei due trattati tradotti in arabo ‒ La misura del cerchio e Della sfera e del cilindro ‒ poteva però aver messo sulla strada di questa riscoperta un matematico della statura di Ṯābit ibn Qurra. Inoltre, le somme integrali di quest'ultimo sono più generali di quelle di Archimede: gli intervalli che egli prende nelle suddivisioni non sono necessariamente uguali. Riguardo allo studio del paraboloide, dove procede sempre per somme integrali, egli non considera, come Archimede, cilindri di altezza uguale, bensì un cono e tronchi di cono che hanno altezze che stanno tra loro in un rapporto pari a quello tra i numeri dispari della serie naturale (cominciando da 1). Era dunque prevedibile che nel periodo successivo, durante il quale la ricerca matematica si intensifica e si sviluppa rapidamente, i matematici cercassero di migliorare le dimostrazioni dei predecessori e di sviluppare entrambi i metodi delle somme integrali e delle trasformazioni geometriche.

Il primo che avanza su questa strada è al-Māhānī (m. 880 ca.). Egli riprende la misura della parabola per darne una dimostrazione molto più breve di quella di Ṯābit ibn Qurra. Purtroppo il testo di al-Māhānī è introvabile, seppure esiste ancora; non possiamo quindi farcene un'idea precisa. Il secondo erede è il nipote di Ṯābit ibn Qurra, Ibrāhīm ibn Sinān (296-335/908-946). Matematico geniale, dalla breve vita, non accettava, come egli stesso diceva, che al-Māhānī "avesse compiuto uno studio più avanzato di quello di mio nonno, senza che tra di noi vi fosse qualcuno che lo superasse". Vuole dare perciò una dimostrazione più breve non solo di quella del nonno, che come abbiamo detto richiedeva venti lemmi, ma anche di quella di al-Māhānī.

Ibrāhīm ibn Sinān scrive dunque il Kitāb fī misāḥat al-qiṭ῾ al-mukāfi᾽ (Dalla misura della parabola), un breve trattato particolarmente conciso ed elegante. L'idea centrale del suo scritto, che egli tiene a dimostrare fin dall'inizio, è che una trasformazione affine conserva la proporzionalità delle aree. Gli bastano allora due lemmi e una sola proposizione per completare lo studio.

Il primo lemma afferma quanto segue. Dati due poligoni convessi A=(A0, A1,…, A_n) e B=(B0, B1,…, B_n) si proiettino i punti A1,…, A_n−1 su A0A_n parallelamen te ad A_n−1A_n nei punti A′1,…, A′_n−1=A_n, e i punti B1,…, B_n−1 su B0B_n parallelamente a B_n−1B_n nei punti B′1,…, B′_n−1=B_n. Se si ha:

,

allora si ha il seguente rapporto di proporzionalità tra aree di triangoli e aree di poligoni:

Nella dimostrazione egli procede con la trasformazione T definita nell'enunciato. Si tratta di una trasforma zione affine, e dimostra che essa conserva il rapporto tra le aree nel caso dei triangoli e dei poligoni.

Il secondo lemma recita come segue: il rapporto tra le aree di due settori parabolici è uguale al rapporto delle aree dei due triangoli a essi associati. In esso egli dimostra che una trasformazione affine conserva il rapporto tra l'area di un settore parabolico e quella di un triangolo associato e il rapporto tra i loro omologhi. La proprietà soggiacente è infatti la conservazione dei rapporti tra le aree (anche di figure curvilinee) per trasformazioni affini. A questo scopo utilizza l'assioma di Archimede per dimostrare che è possibile inscrivere in un settore parabolico un poligono la cui area differisce, di tanto poco quanto si vuole, da quella della parabola. Stabilito ciò, il calcolo del rapporto tra l'area di un settore parabolico e quella del triangolo associato non richiede più procedimenti infinitesimali, ma solo il fatto che questo rapporto non dipende dal settore considerato; ed è quanto dimostra nella seguente proposizione: l'area di un settore parabolico è pari a 4/3 dell'area del triangolo a esso associato. La strategia di Ibn Sinān, per migliorare la dimostrazione del nonno e ridurre il numero di proposizioni da venti a tre, si basa sulla combinazione di trasformazioni affini e metodi infinitesimali.

Anche al-Qūhī (seconda metà del X sec.) riduce a tre le 36 proposizioni stabilite da Ṯābit ibn Qurra per il calcolo del volume del paraboloide di rivoluzione. Tuttavia, se Ibn Sinān segue la via geometrica, quella delle trasformazioni, presente nell'opera di Ṯābit ibn Qurra, al-Qūhī prende l'altra strada, anch'essa presente nell'opera di Ṯābit ibn Qurra, che lo porta a riscoprire le somme integrali contenute nei libri di Archimede che i matematici arabi non conoscevano.

Per il paraboloide di rivoluzione, Archimede considera infatti cilindri di uguale altezza, mentre Ṯābit ibn Qurra ricorre a tronchi di cono adiacenti, le cui basi determinano una suddivisione del diametro della parabola, che genera il pa raboloide; i segmenti della suddivisione sono proporzionali ai numeri dispari a partire da 1 e le altezze sono uguali ai segmenti di questa suddivisione. Al-Qūhī, per ridurre il numero delle proposizioni dimostrate da Ṯābit ibn Qurra, ritrova indipendentemente le somme integrali così come figurano in Archimede. Il suo metodo differisce del resto da quello di Archimede solo in qualche dettaglio, in particolare quando occorre dimostrare che la differenza tra cilindri inscritti e circoscritti si può rendere piccola a piacere. Ricordiamo gli enunciati di queste tre proposizioni.

La prop. 1 è la seguente. Dati un paraboloide di asse XF e una sua suddivisione qualunque con punti di ascissa (b_i)0≤_i≤_n, con b0=0 e b_n=XF, siano (I_i)2≤_i≤_n i volumi dei cilindri inscritti, (C_i)1≤_i≤_n i volumi dei cilindri circoscritti associati a questa suddivisione e V il volume del cilindro associato al paraboloide. Per tutti gli interi positivi n, si ha:

La prop. 2 è la seguente. Data una porzione di paraboloide tra due superfici ordinate qualunque, siano I e C i volumi dei cilindri inscritti e circoscritti corrispondenti. Se si taglia questa porzione con una superficie ordinata equidistante dalle due precedenti, si ottengono due cilindri inscritti di volumi I1 e I2 e due cilindri circoscritti omologhi di volumi rispettivi C1 e C2; si ha:

,

con C−I il volume dell'anello HGEC, con C1−I1 il volume dell'anello NLMC e con C2−I2 il volume dell'anello LKGS. La dimo strazione di questa proposizione è la seguente: se si parte dalla suddivisione dell'asse XF con punti di ascissa (b_i)0≤_i≤_n, con (I_i)1≤_i≤_n, (C_i)1≤_i≤_n e I1=0 i volumi dei cilindri omologhi, e se si considera poi la successione (c_j)0≤_j≤2_n, con b0=c0, b_n=c2_n, c2_i+1=(b_i+b_i+1)/2 e (I′_j)1≤_j≤2_n e (C′_j)1≤_j≤2_n i volumi dei cilindri omologhi associa ti a questa suddivisione, si ha

Nella terza proposizione si dimostra che, se P è il volume di una porzione di paraboloide e V quello del cilindro a esso associato, si ha P=V/2. Se denotiamo con (I^q_i) _{1≤i≤n∙2^q} e (C^q_i) _{1≤i≤n∙2^q} i volumi dei cilindri associati alla suddivisione, si ha, in base alla proposizione precedente, che

,

per n fissato e q un qualunque intero positivo non nullo. Ciò permette ad al-Qūhī, grazie a un'estensione della prop. 1 del Libro X degli Elementi di Euclide, di affermare che a partire da un certo numero di operazioni si ha:

o, in un altro linguaggio, dimostra che, per ogni ε>0, esiste N tale che per ogni q>N si ha la [53]. Ma:

,

da cui

Ora, se P=(V/2)+ε, si ha

,

ciò che è impossibile per la prop. 1. Se P=(V/2)−ε, si ragiona nello stesso modo in quanto:

,

da cui

,

da cui

,

e ciò è impossibile sempre in relazione alla prop. 1. Si ha dunque P=V/2.

La dimostrazione di al-Qūhī è molto rapida grazie alla prop. 1 che confronta direttamente le somme dei cilindri inscritti o circoscritti al volume del grande cilindro, senza che vi sia bisogno di calcolare queste somme come invece fa Archimede riportando il calcolo a una somma di grandezze in progressione aritmetica. La dimostrazione di questa proposizione si basa sulle disuguaglianze u_i−u_i−1⟨2C_i e u_i−u_i−1>2I_i che si ottengono considerando cilindri uguali come QGHR e SBCO che non sono né inscritti né circoscritti, e dunque non sono dati a priori. La prop. 2 stabilisce che se si raffina la suddivisione dividendo a metà i singoli intervalli, l'eccesso dei cilindri circoscritti rispetto ai cilindri inscritti viene diviso per 2. Essa ha lo stesso ruolo della prop. 19 del libro di Archimede Conoidi e sferoidi.

Il metodo di al-Qūhī assomiglia, per l'uso delle somme integrali, a quello di Archimede, ma l'applicazione è piuttosto diversa. È come se al-Qūhī avesse riscoperto l'uso delle somme integrali.

Gli ultimi sviluppi

Partendo dai Banū Mūsā e soprattutto da Ṯābit ibn Qurra, Ibn Sinān segue il filone di ricerca che unisce efficacemente trasformazioni geometriche e tecniche infinitesimali, mentre al-Qūhī riscopre, con i miglioramenti che abbiamo visto, i metodi delle somme integrali. Essi forniscono in tal modo ai loro successori non soltanto una diversa prospettiva di ricerca in geometria infinitesimale, ma anche altri mezzi, e non tarderanno a sfruttare e a riprendere i problemi risolti dai loro predecessori aggiungendone di nuovi.

Il primo ad aver preso questa strada sembra essere stato Ibn Sahl. Egli riprende ancora una volta la quadratura della parabola; il suo trattato è purtroppo ancora introvabile, ma dalla posizione che occupava tra i matematici dell'epoca, dai vari contributi che abbiamo ricostruito e dalla conoscenza che aveva dei lavori di al-Qūhī, possiamo desumere che procedesse per somme integrali. Una congetturra che ci sembra assai verosimile non soltanto per le ragioni dette, ma anche perché Ibn al-Hayṯam (m. dopo il 1040), suo successore, riprenderà la misura della sfera e del paraboloide senza fare riferimento a quella della parabola, come se ciò fosse già stato compiuto con lo stesso metodo. A Ibn al-Hayṯam toccherà portare al punto culminante questa tradizione iniziata un secolo e mezzo prima. Con lui, come vedremo, il calcolo delle superfici curvilinee e dei volumi raggiungerà un livello paragonabile a quello che, sotto altri climi, si incontrerà agli inizi del XVII secolo.

Egli riprende la dimostrazione del volume del paraboloide di rivoluzione. Non si ferma però qui, ma determina anche il volume del paraboloide generato dalla rotazione di una parabola attorno a un'ordinata. Riprende poi anche il calcolo del volume della sfera con lo stesso metodo. Ma prima di esporre il suo procedimento, il più possibile brevemente, ricordiamo un aspetto fondamentale dell'opera di questo matematico, che era anche fisico e astronomo. Se i suoi predeces sori, come al-Qūhī, hanno trattato il problema delle determinazioni infinitesimali per le superfici curvilinee e i volumi, e se essi hanno anche ripreso la questione del centro di gravità di queste figure, Ibn al-Hayṯam si occuperà allora dell'insieme dei problemi sollevati in questo campo: determi na zioni infinitesimali, centri di gravità, problemi isoperimetrici, angolo solido. Egli si dedicherà anche a un altro argomento legato, almeno indirettamente, a questi: le lunule. Inoltre, nel corso di queste ricerche, come pure di altre, incontra veri e propri problemi differenziali. È come se egli avesse voluto attraversare la maggior parte delle regioni che costituiranno più tardi il continente dell'analisi.

Il trattato di Ibn al-Hayṯam Maqāla fī misāḥat al-muǧassam al-mukāfi᾽ (Misura del paraboloide) è di struttura semplice ma significativa. Nell'introduzione, dove ricorda i lavori dei suoi predecessori Ṯābit ibn Qurra e al-Qūhī, egli rimprovera al primo di "aver seguito una strada priva di un piano e di essersi limitato nelle sue spiegazioni a percorrere un cammino lungo e laborioso" (p. 208), e al secondo semplicemente che il suo trattato "contiene solo la dimostrazione della misura di uno dei due tipi di paroboloide" (ibidem). A questa introduzione, nella quale inquadra il proprio libro, segue una prima trattazione interamente dedicata ai lemmi aritmetici necessari per le dimostrazioni. Affronta successivamente le parti dedicate al paraboloide di rivoluzione e a quello di secondo tipo, per poi concludere con la discussione del metodo applicato in questo capitolo.

Egli comincia dimostrando una regola generale, mediante una ricorrenza finita, per il calcolo delle somme di n interi elevati a una potenza i qualunque. La regola si esprime con l'uguaglianza

,

che gli permette di stabilire una disuguaglianza necessaria per l'insieme del procedimento:

La dimostrazione di questo lemma è lunghissima; mostra tuttavia la portata della ricerca aritmetica in questo campo e altresì il suo virtuosismo matematico.

Ibn al-Hayṯam passa poi alla determinazione del volume del paraboloide di rivoluzione. Considera tre casi, a seconda che l'angolo ACB sia retto, acuto od ottuso. Consideriamo, con qualche particolare, il primo caso, seguendo il procedimento dell'autore. Se V è il volume del cilindro circoscritto e v quello del paraboloide, dimostriamo che v=V/2. Procediamo per assurdo e supponiamo, in primo luogo, che sia v>1/2 V, cioè v−(V/2)=ε. Sia M il punto di mezzo di AC e si tracci MU parallelo a BC e che tagli la parabola in E e BH in U. La parallela SEO′ ad AC taglia BC in O′ e AH in S. Denotando con [EC] il solido generato dalla rotazione della superficie MCO′E e con analoghi simboli gli altri solidi, si ha:

Iterando la costruzione a partire dal punto L, punto di mezzo di AM, e poi dal punto K, punto di mezzo di MC, si ha:

dunque

Iterando la costruzione per i punti O, P, N, J, punti di mez zo, rispettivamente, di AL, LM, MK, KC, la somma degli otto solidi sarà uguale alla metà di [62], cioè 1/8 V. Si procede nello stesso modo, vale a dire togliendo i solidi di tipo [60] e [62] dal cilindro circoscritto. Si sarà tolto allora da V successivamente:

e così di seguito. Dopo un numero finito di operazioni si arriva necessariamente a un resto minore di ε, per il lemma 1 del Libro X degli Elementi di Euclide (o per il teorema di Ibn al-Hayṯam).

Supponiamo che la suddivisione della figura corrisponda al momento nel quale il resto è inferiore a ε. Sia V_n il volume dei solidi che restano dopo n passi, dunque V_n⟨ε, e v_n il volume della parte di questi solidi interni al paraboloide; allora v_n⟨V_n e v_n⟨ε, e, per l'ipotesi, v−v_n>1/2V. Ma per le proprietà della parabola abbiamo:

da cui BC2=2EM2. Analogamente,

da cui JE²_j+OE²_o=BC²=2EM². Si dimostra analogamente che KE²_k+LE²_l=BC²=2EM², e così di seguito. Se dunque deno tia mo con E0=A, E1, E2,…, E_n=B (con n=2^m), i punti della parabola corrispondenti ai punti dell'asse F0=A,…, F_n/2=M,…,F_n=C, ne segue

e dunque

Siano ora

le aree dei dischi di raggio E_iF_i e S_n l'area del disco di raggio E_nF_n=BC, si ha:

Denotiamo con W_i il volume dei cilindri di base S_i e altezza h=1/n AC, e con W_n il volume del cilindro di base S_n e altezza h. Si ha allora:

,

ma

in quanto V=nW_n, e dunque

Ma si ha anche

,

il che è impossibile. Dunque v≤1/2V.

Supponiamo, in secondo luogo, che sia v⟨1/2V, cioè v+ε=1/2 V, e procediamo come in precedenza. Si toglie successivamente la metà del volume del cilindro, poi la metà di ciò che resta, finché il volume che resta V_n non è inferiore a un ε dato a piacere. Sia u_n la parte di V_n esterna al paraboloide; si ha u_n⟨V_n, dunque u_n⟨ε, da cui: v+u_n⟨V/2. D'altra parte, si ha v+u_n =∑ⁿ_i=1W_i, e dunque ∑ⁿ_i=1W_i<V/2. Ma abbiamo dimostrato che ∑^n-1_i=1W_i =(n-1)Wn/2, e si ha anche ∑^n-1_i=1W_i = ∑ⁿ_i=1W_i - W_n, e dunque:

da cui

Ne segue ∑ⁿ_i=1W_i > V/2 che è impossibile per cui v≥1/2V.

Abbiamo così dimostrato che v=V/2 per il caso dell'angolo ACB retto. Ibn al-Hayṯam riporta altri due casi,

e

,

al primo mediante una trasformazione affine: gli assi obliqui si trasformano in assi rettangolari. Più precisamente, egli associa punto per punto la figura in ciascuno dei due casi alla figura del primo, utilizzando la conservazione delle relazioni in queste figure. Si tratta perciò del metodo delle somme integrali e dell'applicazione del metodo di esaustione, che poggia però su una solida base aritmetica.

Lo stile di Ibn al-Hayṯam si rivela in modo lampante quando egli si occupa della seconda specie di paraboloide, quello ottenuto per rotazione della parabola attorno a un'ordinata. Per mettere meglio in risalto la natura del procedimento descriviamo il suo studio in un linguaggio diverso. Consideriamo il paraboloide generato dalla rotazione del settore ABC della parabola di equazione x=ky2 attorno all'ordinata BC. Poniamo AC=c e BC=b. Sia σ_n=(y_i)0≤_i≤2m, con 2^m=n una suddivisione dell'intervallo [0,b] di passo h=b/n. Siano M_i i punti della parabola di ordinata y_i e ascissa x_i, e poniamo r_i=c−x_i (0≤i≤2^m=n). Ne segue che r_i=k(b²-y²_i) = kh²(n²-i²). Indicando con I_n e C_n i volumi dei cilindri inscritti e circoscritti, si ha

ma per la disuguaglianza [59] si ottiene

dove V=πk2b4∙b è il volume del cilindro circoscritto. Sempre in un linguaggio che non è quello di Ibn al-Hayṯam, il calcolo è il seguente. Poiché la funzione g(y)=ky2 è continua in [0,b], denotando con v(p) il volume del paraboloide si ha:

da cui

,

cioè

,

ovvero

,

dove V è il volume del cilindro circoscritto.

Ibn al-Hayṯam si interroga infine sul comportamento dei solidi che approssimano il paraboloide dall'esterno, quando si aumentano indefinitamente i punti di suddivisione. Pone insomma il problema della variazione del rapporto tra questi solidi infinitesimali, cioè le parti interne ed esterne al paraboloide. Per il paraboloide di prima specie i due solidi hanno lo stesso volume, ma ciò non è più vero per quelli di seconda specie. Denotiamo con v_n e u_n i volumi dei piccoli solidi approssimanti interni ed esterni al paraboloide; egli dimostra che

Denotiamo poi con u(m) e W(m) i valori corrispondenti a u e a W alla m-esima suddivisione (n=2^m); egli dimostra che:

e dunque il rapporto cresce quando i punti di suddivisione aumentano. Ci troviamo così in presenza di un orientamento di tipo decisamente infinitesimale e in certo qual modo di teoria delle funzioni. La posta in gioco è esplicita: è il comportamento asintotico di oggetti matematici dei quali si cerca di determinare la variazione.

Dopo questo trattato sui paraboloidi, Ibn al-Hayṯam riprende la misura della sfera in un altro trattato dal titolo Qawl fī misāḥat al-kura (Sulla misura della sfera) nel quale applica lo stesso metodo. Comincia perciò nello stesso modo, premettendo i lemmi aritmetici necessari. Ricorda dapprima che:

e stabilisce poi la disuguaglianza:

Con lo stesso metodo prima utilizzato, egli dimostra che il volume della sfera è uguale a due terzi di quello del cilindro circoscritto. Soffermiamoci ora su questo metodo a partire dal calcolo integrale per coglierne le idee fondamentali. Per determinare il volume di rivoluzione attorno a un dato asse, egli prende fette cilindriche inscritte e circoscritte il cui asse è quello del solido di rivoluzione considerato. Ciò permette approssimazioni per difetto e per eccesso del volume da calcolare mediante somme integrali (somme di Darboux) relative alla funzione corrispondente alla curva che genera il solido di rivoluzione in questione. Per esempio, per il volume della sfera, egli considera

Osserviamo che la funzione f è monotona, di modo che m_i e M_i sono i valori di f agli estremi dell'i-esimo intervallo di suddivisione; la f è definita da

,

per x_i−1≤x≤x_i m_i e M_i essendo i punti di ordinate y_i e y_i−1. D'altra parte, utilizza poi le disuguaglianze I_n⟨v⟨C_n, e dimostra che, per ogni ε>0, esiste N tale che per n≥N si ha v−I_n⟨ε e C_n−v⟨ε; e ciò dimostra che I_n tende a v e lo stesso accade per C_n. In altri termini si ha effettivamente v = ∫^R₀f(x)dx.

Il calcolo di Ibn al-Hayṯam equivale pertanto a quello di un integrale di Cauchy-Riemann semplice.

Questa equivalenza matematica, tuttavia, non deve nascondere il problema seguente: perché Ibn al-Hayṯam, una volta determinati i volumi mediante questo integrale, non ha mai indicato un metodo generale per determinare altri volumi e altre aree? Per rispondere a questa domanda in modo soddisfa cente non basta invocare le necessità che aveva Ibn al-Hayṯam. Nella sua opera di matematica, ottica e astronomia egli non ha mai avuto bisogno di calcolare il volume di un paraboloide, e nemmeno, per esempio, di un iperboloide di rivoluzione. È dunque al metodo stesso che bisogna imputare l'assenza di quella indicazione.

Si può osservare in effetti che Ibn al-Hayṯam, proprio come i suoi predecessori a proposito delle aree, fa sempre appello a un altro solido di volume noto con il quale confrontare il solido in questione. Questa conoscenza preventiva del solido di confronto non è un artefatto del metodo: essa permette a Ibn al-Hayṯam, come ai suoi predecessori, un calcolo effettivo, diretto ed esatto, dei limiti delle somme di Darboux corrispondenti. Ora, nel caso generale, non è detto che questi solidi di confronto esistano, ciò rende gli strumenti matematici che Ibn al-Hayṯam utilizza insufficienti per un calcolo effettivo delle somme di Darboux. Si tratta quindi di un vero e proprio limite interno quello che contrassegna il metodo di Ibn al-Hayṯam. Occorre tuttavia guardarsi dall'esagerare la portata di questo limite, che scom parirà con l'introduzione, in modo ancora più massiccio, del calcolo aritmetico. Se dunque la presenza di un volume di riferimento caratterizza bene la tradizione archimedea, l'orientamento aritmetico, che andava crescendo nella tradizione araba, mostra che non si tratta più strettamente di un'eredità archimedea. Non è solo la geometria a guidare Ibn al-Hayṯam, ma è già l'aritmetica; i lemmi nascono da una concezione aritmetica delle figure geometriche.

In tale studio si può già osservare lo sviluppo dei mezzi e delle tecniche di questa branca nella matematica araba. Si è visto come Ibn al-Hayṯam, nelle sue ricerche sul paraboloide, ottenga risultati che gli storici attribuiscono ad autori come Kepler e Cavalieri. Queste ricerche però si fermano qui, molto probabilmente per la mancanza di un simbolismo efficace.

La quadratura delle lunule

Tra i problemi di determinazione delle aree delle superfici curve, la quadratura esatta delle 'lunule', superfici limitate da due archi di cerchio, è uno dei più antichi. Secondo testimoni vissuti più tardi come Simplicio, il commentatore di Aristotele del VI sec., il problema risale a Ippocrate di Chio, cioè al V sec. a.C. Nel commento alla Fisica di Aristotele, Simplicio riporta un lungo brano di Eudemo, discepolo di Aristotele, che contiene i risultati e i metodi di Ippocrate. Tale passo, che solleva d'altra parte numerosi quesiti filologici e storici, è la sola fonte conosciuta per la storia di questo problema nella matematica greca. Vi si indica anche il contesto nel quale fu posto il problema della quadratura di alcune lunule, in questo caso la quadratura del cerchio.

Circa cinque secoli dopo Simplicio, Ibn al-Hayṯam ritorna più volte sulla questione, dapprima in relazione alla quadratura del cerchio, e poi come problema a sé. Lo riprende in effetti in tre memorie, una sola delle quali è stata studiata fino a oggi, quella sulla quadratura del cerchio, e ne dedica una breve alla quadratura delle lunule. Più tardi si occupa di nuovo dell'argomento, ottenendo risultati che saranno attribuiti ai matematici dei secc. XVII e XVIII. La mancata conoscenza dei lavori di Ibn al-Hayṯam, e in particolare di quest'ultimo trattato, ha portato gli storici a dare, in completa buona fede, giudizi errati sui suoi contributi a queste ricerche.

Tutto indica che il punto di partenza di Ibn al-Hayṯam è il testo attribuito a Ippocrate di Chio. Nel suo primo trattato Qawl fī 'l-hilāliyyāt (Trattato sulle lunule) egli comincia dicendo "quando considerai […], la figura delle lunule uguale a un triangolo, menzionata dagli antichi […]". Più tardi, in un secondo trattato Maqāla mustaqṣāt fī 'l-aškāl al-hilāliyya (Trattato esaustivo sulle figure delle lunule), Ibn al-Hayṯam ricorda così il suo primo libro: "Ho composto un breve trattato sulle lunule secondo metodi particolari" (Rashed 1993a, p. 102). I risultati di Ippocrate di Chio sono inoltre riportati nei suoi lavori. Ibn al-Hayṯam ne è venuto a conoscenza grazie al commento di Simplicio alla Fisica di Aristotele, che allora sarebbe stato tradotto in arabo? Non abbiamo documenti che ci permettano di rispondere con esattezza a questa domanda. Nel primo lavoro Ibn al-Hayṯam parla degli 'antichi', ma non riporta alcuna delle figure di Ippocrate. Tuttavia, nel suo primo risultato egli generalizza leggermente una proposizione di Ippocrate, citata da Simplicio basandosi su un testo di Alessandro di Afrodisia; ciò complica notevolmente il problema. Si tratta della prop. 3 che figura anche nella sua opera sulla quadratura del cerchio (Qawl fī tarbī῾ al-dā᾽ira), e nel suo secondo trattato (prop. 8). Comunque sia, veniamo ora ai due lavori di Ibn al-Hayṯam.

Il procedimento adottato in entrambi consiste nello studio delle lunule limitate da archi qualunque e nella ricerca di equivalenze tra superfici. L'autore introduce dei cerchi equivalenti a settori di cerchio dati nel problema ed espressi in frazioni di quest'ultimo. Giustifica l'esistenza dei cerchi introdotti, che aggiunge o sottrae a superfici poligonali per ottenere una superficie equivalente a quella di una lunula, o alla somma di due lunule.

Nel primo breve trattato egli prende le mosse, nelle tre propp. 1, 2 e 5, da un semicerchio ABC, per studiare le lunule L1 e L2 limitate da un arco AB o BC e da un semicerchio. Suppone che l'arco AB sia uguale a un sesto di circonferenza e stabilisce i seguenti risultati:

dove L3 è una lunula simile a L1 e tale che L3=2L1, mentre C(ABC) e tr(ABC) denotano rispettivamente il cerchio ABC e il triangolo ABC.

Nella prop. 3 generalizza leggermente la dimostrazione del risultato di Ippocrate di Chio, considerando un punto qualunque B del semicerchio ABC: L1+L2=tr(ABC); e nella prop. 4 studia il rapporto tra due lunule simili. Si osservi come in queste proposizioni le lunule L1 e L2 che intervengono sono quelle associate ai tre semicerchi ABC, AEB e BGC.

Questo primo trattato si presenta dunque nel solco delle ricerche di Ippocrate di Chio. Lo stesso accade per la parte relativa alle lunule dell'opera sulla Fī tarbī῾ al-dā᾽ira. Come Ippocrate, Ibn al-Hayṯam utilizza la proporzionalità tra area del cerchio e quadrato del diametro, e il teorema di Pitagora. In entrambi i casi si studia la lunula associata al triangolo rettangolo isoscele. Anche se il ragionamento di Ibn al-Hayṯam è un po' più generale, si tratta di una generalizzazione che fondamentalmente non modifica la somiglianza tra il suo procedimento e quello di Ippocrate. Segnaliamo, per completezza, che ciò che è importante nel Fī tarbī῾ al-dā᾽ira non sono i risultati sulle lunule che, come nel primo trattato, egli studia, ma la differenza che egli stabilisce tra l'esistenza di un quadrato equivalente al cerchio ‒ cioè, nel linguaggio di oggi, l'esistenza di un rapporto trascendente ‒ e la costruibilità di questo quadrato o di questo rapporto.

La situazione è molto diversa nel secondo trattato, la Maqāla mustaqṣāt fī 'l-aškāl al-hilāliyya. Non soltanto ottiene qui risultati più generali, ma il procedimento non è lo stesso. Riprende il problema della quadratura delle lunule, lo sposta sul piano della trigonometria e cerca di dedurre i diversi casi come altrettante proprietà di una funzione trigonometrica che sarà riconosciuta molto più tardi da Euler. Fin dall'inizio riconosce esplicitamente che il calcolo delle aree delle lunule fa intervenire somme e differenze di aree di settori circolari, e di triangoli il cui confronto richiede il confronto di rapporti tra angoli e rapporti tra segmenti. È per questa ragione che egli comin cia con lo stabilire quattro lemmi relativi al triangolo ABC, rettangolo in B nel primo lemma e ad angolo ottuso negli altri tre, i quali dimostrano ormai che il punto essenziale della ricerca è diventato lo studio della funzione

Si possono allora riscrivere questi lemmi come segue.

a) Se 0⟨C⟨π/4⟨A⟨π/2, allora (sen2C)/C⟨2/π⟨(sen2A)/A; è chiaro che se C=A=π/4, allora (sen2C)/C=(sen2A)/A=2/π.

b) Sia π−B=B1; se C⟨π/4⟨B1⟨π/2,(sen2C)/C⟨(sen2B1)/B1.

c) Se A≤π/4, allora (sen2A)/A⟨(sen2B1)/B1.

d) Qui si propone di studiare il caso A>π/4. Lo studio è però incompleto: Ibn al-Hayṯam dimostra che, dato A, si può trovare B0 tale che

Questo studio incompleto sembra gli abbia impedito di vedere l'uguaglianza

Si noterà che questi lemmi, legando il problema della quadratura delle lunule alla trigonometria, ne cambiano lo status e permettono di unificare i vari casi particolari. Ma l'incompletezza già segnalata nasconde la possibilità dell'esistenza di lunule quadrabili. Veniamo ora brevemente alle proposizioni del secondo trattato di Ibn al-Hayṯam.

In nove proposizioni, dalla 8 alla 16, i lemmi sono associa ti a coppie, e in tutti i casi i tre archi ABC, AEB e BCG sono simili. Siano O, O1 e O2 i centri dei cerchi corrispondenti.

Poniamo:

con β≤β′ e β+β′=α.

La lunula L1 è caratterizzata da (α, β) e la lunula L2 da (α, β′). Si considera allora il caso α=π/2; e si hanno le seguenti proposizioni:

1) per ogni coppia (β, β′) tale che β+β′=π/2, si ha L1+L2=tr(ABC);

2) per β=β′=π/4, si ha L1=L2=tr(ABC)/2; in questo caso, α/β=2/1, e si ha la sola lunula quadrabile studiata da Ibn al-Hayṯam. Per β⟨β′ si ha

il cerchio N dipende dal rapporto α/β;

3) per β=π/6, si ha L1=(1/2) tr(ABC)−(1/24)C(ABC); in tal caso α/β=3/1. Per β′=π/3, si ha L2=(1/2) tr(ABC)+ +(1/24)C(ABC), e in questo caso α/β′=3/2.

Fin qui utilizza nelle dimostrazioni soltanto il lemma 1. Per stabilire la proposizione seguente ricorre agli altri tre. L'idea direttrice consiste nel partire dai punti M e N sulla corda AC tali che

,

e definire un punto P su AB e un punto Q su BC tali che NP è parallelo a OA e MQ è parallelo a OC; i risultati non possono infatti essere stabiliti a partire dal triangolo ABC come nelle proposizioni precedenti.

Per ogni coppia (β, β′) tale che β+β′⟨π/2, definisce allora due cerchi (K) e (Z) tali che

considera poi i casi seguenti: se β=β′, si ha (Z)=(K)/2, L1=L2, e L2+(Z)=tr(OQB)=tr(OPB); se β′⟨π/4, si ha (Z)⟨(K) e L2+(K)−(Z)=tr(OQB); e se β′>π/4, si può avere (Z)⟨(K), L2+(K)−(Z)=tr(OQB) e L2⟨tr(OQB), oppure (Z)=(K) e L2=tr(OQB), o ancora (Z)>(K), L2=tr(OQB)+(Z)−(K) e L2>tr(OQB). Egli illustra questi risultati con alcuni esempi; dimostra poi le seguenti proposizioni.

4) Se α=π/3, β=β′=π/6, α/β′=2/1, si ha:

5) Se α=π/3, β=π/12, β′=π/4, α/β=4/1, α/β′=4/3, in tal caso il cerchio che interviene non è parte del cerchio ABC.

6) Se α=π/3+π/8, β=π/8, β′=π/3, α/β=11/3, α/β′=11/8, in questo caso il cerchio che interviene non è una parte del cerchio ABC.

Nelle proposizioni seguenti, a esclusione della prop. 21, studia le figure composte di somme o di differenze di lunule, di segmenti e triangoli. Nella prop. 21 egli indica una proprietà della lunula i cui due archi appartengono a due cerchi uguali, proprietà che risulta dalla traslazione che mette in relazione i due cerchi e che studia nel trattato Fī 'l-taḥlīl wa-'l-tarkīb (Sull'analisi e la sintesi).

Con questo secondo trattato di Ibn al-Hayṯam lo studio della quadratura delle lunule prende un'altra strada, quella che condurrà più tardi a Euler, spostando il problema verso la trigonometria e riconoscendone in qualche modo la dipendenza dalla funzione [86].

Il problema degli isoperimetri e la ricerca di 'extrema'

Abbiamo sottolineato come la geometria infinitesimale sia apparsa in campi diversi da quello della determinazione di aree e volumi delle figure curvilinee. Uno di questi è lo studio dei problemi isoperimetrici nel piano e nello spazio. Inizialmente legata all'astronomia, tale ricerca se ne allontana sempre di più per diventare un capitolo della geometria infinitesimale. Non è questa la sede per ripercorrere nei particolari la storia di questo processo; sarà sufficiente indicarne le linee generali.

Tra le figure piane di dato perimetro, il cerchio ha l'area massima, e tra i solidi di uguale area totale, la sfera ha il volume massimo. È questo l'enunciato del problema della ricerca di extrema, che non ha mai smesso di interessare i matematici e gli astronomi fin dall'Antichità: se questi ultimi ne avevano bisogno per stabilire la sfericità del cielo e del corpo del mondo, i primi si sono messi all'opera verosimilmente per fornire loro la dimostrazione che mancava.

Il problema degli isoperimetri, secondo la testimonianza di Simplicio, filosofo del V sec., è antico. Egli, infatti, scrive: "È stato dimostrato, non soltanto prima di Aristotele, tanto che questi se ne serve come [proposizione] dimostrata, ma anche da Archimede, e in modo più particolareggiato (πλατύτεϱον) da Zenodoro che, tra le figure isoperimetriche, la più estesa è tra le figure piane il cerchio, e tra i solidi la sfera" (Simplicii in Aristotelis de Coelo Commentaria, VII, 4/2, rr. 12-17).

Questo testo importante, anche se tardo, mostra, come ha osservato W. Schmidt (1901), che le proposizioni fondamentali erano note prima di Zenodoro. è questa idea che spingerà in seguito J. Mogenet (1961) ad attribuire a Zenodo ro soltanto il merito di una prima formulazione della teoria degli isoperimetri, una teoria a pieno titolo, e a prendere lo spunto da ciò per datare l'epoca del matematico al III sec. a.C. La questione resta controversa, oggi come allora; tutto ciò che si può dire al momento è che Zenodoro ha vissuto dopo Archimede e prima di Pappo, cioè tra il II sec. a.C. e il III d.C.

Un intervallo di mezzo millennio non può che favorire le discussioni, mancando precisazioni ulteriori che ancora si aspettano. Ma questi dibattiti, già cominciati all'inizio del secolo scorso, non hanno impedito agli storici di accordarsi per attribuire allo stesso Zenodoro di aver trattato il problema matematico, e di averne dato la dimostrazione. Fortunatamente, Teone di Alessandria (IV sec. d.C.) riassume, nel Commento al libro primo dell'Almagesto, il libro di Zenodoro. Dopo aver posto il problema isoperimetrico, Teone annuncia testualmente che "lo dimostrerà in modo abbreviato, tratto dalla dimostrazione di Zenodoro, nel trattato sulle figure isoperimetriche" (p. 33). Teone si rifà proprio a Zenodoro per commentare la celebre formula di Tolomeo nel Libro I dell'Almagesto: "Poiché tra le diverse figure aventi uguale perimetro quelle che hanno più lati sono più grandi, tra le figure piane è il cerchio che è il più grande, e tra quelle solide è la sfera, e il cielo è il più grande dei corpi" (ed. Heiberg, p. 13, rr. 16-19).

I commenti all'Almagesto, già dall'epoca di Teone, non potevano ormai più passare sotto silenzio una formulazione come questa, che riguarda un'idea fondamentale dell'astronomia, della cosmogonia e della filosofia: la sfericità del cielo e del corpo del mondo. Dovevano darne una dimostrazione. Altri matematici si sono interessati naturalmente a questo problema, come Erone di Alessandria e Pappo di Alessandria (IV sec. a.C.), nel Libro V della Collezione. Il Commento di Teone, come pure lo stesso Almagesto, che erano noti agli astronomi e ai matematici del IX sec., stimolarono una nuova tradizione di ricerca sugli isoperimetri che comincia con al-Kindī, il quale afferma di aver considerato il problema "nel [suo] libro sulle sfere". Scrive infatti nel Fī 'l- ṣinā῾at al-῾uẓmā (Sulla grande arte): "Analogamente, poiché la più grande delle figure nel cerchio avente i lati uguali è quella che ha più angoli, e la più grande figura solida avente superfici piane e uguali è la sfera, come abbiamo spiegato nel nostro libro Sulle sfere, il cielo è dunque più grande di tutti gli altri corpi, ed è sferico perché deve avere la figura più grande" (Istanbul, Aya Sofya, 4860, f. 59v).

Il biografo e bibliografo del XIII sec., Ibn Abī Uṣaybi῾a cita tra le opere di al-Kindī un titolo dedicato esplicitamente a questo problema: Fī anna al-kura awsa῾ al-aškāl al-muǧassama (La sfera è la più grande figura solida). In ogni caso, al-Ṣinā῾at al-῾uẓmā di al-Kindī risente fortemente dell'influenza di Teone.

Di questa tradizione faranno parte, a diverso titolo, numerosi astronomi come ǧĀbir ibn Aflaḥ e matematici come Ibn Hūd. Ma due studiosi trasformeranno la ricerca in questo campo, ciascuno a suo modo: al-Ḫāzin e Ibn al-Hayṯam. Sono le figure principali di cui al momento abbiamo conoscenza. La lettura e l'analisi degli scritti di questi matematici metteranno in luce la grande distanza che li separa: mentre al-Ḫāzin sviluppa il passato, Ibn al-Hayṯam, portandolo a compimento, lambisce l'avvenire.

Al-Ḫāzin: introduzione matematica all'Almagesto

Anche Abū Ǧa῾far al-Ḫāzin (X sec.) scrisse uno Šarḥ al-maqāla al-ūlā min al-Maǧisṭī (Commento al Libro I dell'Almagesto). È verosimilmente a proposito della celebre affermazione di Tolomeo prima citata che egli include in quest'opera un trattato con lo scopo di darne una dimostrazione rigorosa. Al-Ḫāzin è chiaro in proposito: vuole stabilire l'enunciato di Tolomeo non per mezzo di calcoli (ḥisāb) ma per via geometrica. Un esame del testo dimostra chiaramente che, se pure al-Ḫāzin conosceva i risultati di Zenodoro nel riassunto di Teone, segue però un'altra strada, come vedremo. L'idea direttrice di al-Ḫāzin, della quale egli è perfettamente conscio, è la seguente: tra tutte le figure convesse di un dato tipo (triangolo, rombo, parallelogramma, ecc.), la più simmetrica realizza un 'estremo' per una certa grandezza (area, rapporto d'area, perimetro, ecc.). Si procede come segue: si fissa un parametro e si fa variare la figura simmetrizzandola rispetto a una data retta. Per esempio, fissando il perimetro di un parallelogramma lo si trasforma in un rombo rendendolo simmetrico rispetto a una diagonale: nel processo di trasformazione l'area aumenta. Non soltanto questa idea distingue il contributo di al-Ḫāzin da quelli dei suoi predecessori, ma dimenticarla significherebbe lasciarsi sfuggire il significato di questo contributo.

Il trattato di al-Ḫāzin ha una struttura semplice. In una prima parte l'autore si occupa degli isoperimetri nel piano e nella seconda nello spazio. Entrambe le parti dipendono da nozioni non precisate e da assiomi non enunciati. In particolare la nozione di convessità: tutti i poligoni e i poliedri considerati sono convessi. Tra gli altri assiomi vi sono i seguenti: (A1) se un poligono convesso è inscritto in un cerchio, allora il suo perimetro è inferiore a quello del cerchio; (A2) se un poligono convesso è circoscritto a un cerchio, allora il suo perimetro è superiore a quello del cerchio; (A3) se un poliedro convesso è inscritto in una sfera, allora la sua area è inferiore a quella della sfera; e (A4) se un poliedro convesso è circoscritto a una sfera, allora la sua area è superiore a quella della sfera. Questi assiomi sono necessari per dimostrare rigorosamente un lemma importante (l'ottavo) e una proposizione (la 19). Consideriamo brevemente le due parti del trattato.

Nella prima parte, prima di stabilire il teorema degli isoperimetri, dimostra otto lemmi. I primi quattro sono relativi ai triangoli isosceli ed equilateri, e mostrano che l'area di un triangolo equilatero è maggiore di quella di un qualunque triangolo isoscele che ha lo stesso perimetro. Il quinto mostra che l'area di un triangolo equilatero è maggiore di quella di un qualunque triangolo che ha lo stesso perimetro. Nel corso della dimostrazione stabilisce un risultato già espresso da Zenodoro e da Pappo, e cioè che, tra le figure isoperimetriche e che hanno un numero uguale di lati, la più grande è quella che ha lati e angoli uguali. Nel lemma 6 egli confronta il parallelogramma con un quadrato avente lo stesso perimetro. Nel lemma 7 considera l'esempio di un pentagono regolare, ne deduce uno irregolare avente lo stesso perimetro e mostra che il secondo ha area più piccola del primo.

Fermiamoci un momento e paragoniamo questo procedimento con quello di Zenodoro. Quest'ultimo comincia con il confrontare un triangolo qualunque e uno isoscele aventi una base comune e lo stesso perimetro per arrivare al seguente lemma: la somma di due triangoli isosceli simili che hanno basi diverse è maggiore della somma di due triangoli isosceli non simili ma con gli stessi perimetri dei due triangoli simili. Qui per 'stesso perimetro' bisogna intendere che le somme dei lati, basi escluse, sono uguali. Questo lemma di Zenodoro non è però corretto, ed è sorprendente che né Pappo né Teone abbiano notato l'errore. Questo lemma equivale infatti a trovare il massimo di ax+by sotto la condizione

È necessario dunque che sia ax′+by′=0, da cui x′=b e y′=−a, e derivando la seconda uguaglianza,

ponendo x=au e y=bv si ha:

mentre l'enunciato richiede che sia u=v. Questo errore è forse il motivo della scelta del metodo operata da al-Ḫāzin?

Nel lemma 8, infine, passa ai poligoni convessi, ammettendo l'esistenza di un cerchio inscritto e di uno circoscritto.

Tutto è ora pronto per stabilire la proprietà isoperimetrica dei poligoni regolari prima di passare infine al teorema sul cerchio. Dimostra dunque dapprima che, se due poligoni regolari P1 e P2 hanno rispettivamente n1 e n2 lati, con n1>n2, e lo stesso perimetro, allora l'area di P1 è maggiore di quella di P2. Stabilisce quindi il teorema: tra tutte le figure piane, poligoni regolari convessi e cerchi, aventi lo stesso perimetro, il cerchio ha l'area più grande. Per quanto riguarda gli isoperimetri nel piano egli procede dunque (a) per confronto di poligoni regolari con lo stesso perimetro e un diverso numero di lati; (b) per confronto di un poligono regolare e un cerchio dello stesso perimetro mediante un poligono simile circoscritto a un cerchio. Questo modo di procedere è comune ad al-Ḫāzin e a Zenodoro. È un'impostazione che potremmo definire statica, nel senso che da una parte abbiamo il poligono dato e dall'altra il cerchio. Più tardi Ibn al-Hayṯam utilizzerà (a) per stabilire (b), considerando il cerchio come limite di una successione di poligoni regolari. Si tratta quindi di un'impostazione dinamica. In altre parole, anche se il metodo di al-Ḫāzin è diverso da quello di Zenodoro o di Pappo, esso è dello stesso tipo, mentre quello di Ibn al-Hayṯam è di un altro tipo.

La seconda parte del trattato di al-Ḫāzin riguarda lo stesso problema di estremo, ma nello spazio. Anche questa parte consta di nove lemmi sull'area e il volume della piramide, del cono e del tronco di cono. Nel primo lemma si considera l'area laterale di una piramide regolare; nel secondo, il volume di una piramide che ammette una sfera inscritta; nel terzo, l'area laterale e il volume di un cono di rivoluzione; nel quarto si considera il problema seguente: dato un cerchio C, costruire due poligoni simili di aree S1 e S2, uno circoscritto a C e l'altro inscritto in C, e tali che S1/S2=k (il rapporto dato). Nel quinto lemma egli dà un'altra espressione dell'area laterale del cono, per poi passare nel sesto lemma all'area del tronco di cono. Da quest'ultimo si deduce allora il settimo, che si enuncia: se una linea poligonale regolare è inscritta in un cerchio di area S1 e circoscritta a uno di area S2, l'area S della superficie generata dalla rotazione di questa linea attorno a uno dei suoi assi soddisfa 4S2⟨S⟨4S1.

Ricordiamo che nelle proposizioni dalla 27 alla 30 dell'opera Della sfera e del cilindro Archimede ottiene gli stessi risultati per un solido definito a partire da un poligono regolare con un numero di lati multiplo di 4. I Banū Mūsā tratteranno poi lo stesso problema per un solido definito da una linea poligonale inscritto in un semicerchio e con un numero pari di lati (propp. 12 e 13). È precisamente il caso trattato da al-Ḫāzin. Giovanni di Tinemue studia d'altra parte, nella prop. 5 lo stesso risultato a partire da un poligono regolare inscritto in un cerchio e con un numero di lati multiplo di 4 o semplicemente di 2.

Al-Ḫāzin termina stabilendo le due proposizioni fondamentali. Nella prima mostra che l'area S della sfera è uguale a quattro volte l'area di un cerchio massimo. Archimede aveva dato lo stesso teorema nella prop. 33 del Libro I di Della sfera e del cilindro e i Banū Mūsā nella prop. 14 del trattato Kitāb ma῾rifat misāḥat al-aškāl al-basīṭa wa-'l-kuriyya (Libro per conoscere l'area delle figure piane e sferiche). Nella seconda proposizione al-Ḫāzin riprende la determinazione del volume della sfera V=(1/3)RS, con R raggio di un cerchio massimo e S l'area. Per stabilire questa proposizione applica la riduzione all'assurdo e utilizza la prop. 17 del Libro XII degli Elementi, seguendo un procedimento analogo a quello usato dai Banū Mūsā.

Dimostra infine il teorema che afferma che, tra tutti i solidi convessi aventi la stessa area, la sfera ha volume massimo. Sia data una sfera di centro O, raggio R, area S, volume V, e sia dato un poliedro avente la stessa area S, volume V1 e che si suppone circoscritto a un'altra sfera, di raggio R′ e area S′. Allora si ha: V1=(1/3)SR′. L'area S′ è inferiore a quella del poliedro, ossia S>S′, e dunque: R′⟨R e (1/3)SR′⟨(1/3)SR, cioè V1⟨V. Osserviamo che non viene specificato di quale poliedro si tratta, ma la dimostrazione suppone che esso sia circoscritto a una sfera, il caso cioè di un poliedro regolare. La dimostrazione vista non si applica a poliedri o a solidi qualunque.

Come si vede, il procedimento di al-Ḫāzin non è lo stesso nello spazio e nel piano. Questa volta non confronta poliedri aventi la stessa area e un diverso numero di facce, ma perviene al risultato utilizzando la formula che lega il volume della sfera all'area, formula che ottiene approssimando la sfera con poliedri non regolari. Il procedimento di Ibn al-Hayṯam, come vedremo, sarà anche in questo caso completamente diverso.

Ibn al-Hayṯam: una teoria degli isoperimetri

Circa mezzo secolo dopo al-Ḫāzin, Ibn al-Hayṯam riprende lo stesso problema, ma restituendo a esso, per così dire, il suo orizzonte, quello della ricerca sui comportamenti asintotici. Non si tratta quindi più di scrivere un'introduzione all'Almagesto per giustificare la famosa affermazione di Tolomeo nel primo libro di quest'opera, ma di scrivere un trattato interamente dedicato allo studio del problema in sé e di affrontare esplicitamente lo studio di questo aspetto di natura asintotica. Ibn al-Hayṯam si propone in effetti di stabilire che "tra le figure che hanno perimetri simili [e uguali], il cerchio ha la più grande [area], e che tra i poligoni quello che più si avvicina alla forma circolare è più grande di quello che se ne allontana" (Rashed 1993a, p. 394), e più generalmente che tra le figure "solide e piane" quella che si avvicina alla forma circolare "ha una misura più grande di quella che se ne allontana" (ibidem, p. 384). Consideriamo brevemente il procedimento seguito.

Egli risolve la questione isoperimetrica nel piano in tre proposizioni e un lemma. Ecco nell'ordine le tre proposizioni. La prop. 1 afferma che, se p è il perimetro di un cerchio e A l'area, p′ il perimetro di un poligono regolare e A′ l'area, se p=p′, allora A>A′. L'enunciato della prop. 2 è il seguente: dati P1 e P2 due poligoni regolari, con n_i, p_i e A_i, (i=1,2), il numero dei lati, i perimetri e le aree, se p1=p2 e n1⟨n2, allora A1⟨A2. Infine, la prop.3 stabilisce che, dati P1 e P2 due poligoni regolari inscritti nel medesimo cerchio (con le notazioni precedenti), se n1⟨n2, allora p1⟨p2 e A1⟨A2. Per stabilire quest'ultima proposizione dimo stra un lemma che si può enunciare come segue: α/β=senα/senβ, per π/2>α>β.

Per stabilire la proprietà isoperimetrica egli dimostra quindi che l'area di un cerchio è come un 'limite' di una successione crescente delle aree di poligoni regolari. Nella dimostrazione suppone che questo limite esiste, come già ammesso ne La misura del cerchio di Archimede. Egli intraprende quindi un procedimento espressamente 'dinamico' e apparentemente diverso da quello dei suoi predecessori. Ciò può spiegare quanto scrive all'inizio del trattato: "I matematici hanno richiamato questa nozione [di isoperimetria] e l'hanno utilizzata. Tutta via non ci è pervenuta alcuna delle loro dimostrazioni" (ibidem, p. 386). Ora, è poco verosimile che Ibn al-Hayṯam ignorasse i numerosi risultati dei suoi predecessori, compresi quelli di al-Ḫāzin. Piuttosto, tutto sembra indicare che egli volesse far notare al lettore la novità del suo procedimento.

Dopo aver affrontato il problema isoperimetrico nel piano, passa a quello nello spazio (relativo a solidi con superfici equivalenti) che affronta con un procedimento analogo. Il passaggio dal piano allo spazio non è però sempre facile. Sulla sua strada incontra dunque un ostacolo, che gli impedirà di raggiungere il suo scopo, ma non di scrivere un testo matematico che fino alla metà del XVII sec. sarà tra i più avanzati.

Analogamente a quanto fatto nella prima parte del trattato, si propone di dimostrare le due proposizioni seguenti: tra due poliedri regolari a facce simili e con la medesima area totale, quello che ha il maggior numero di facce ha il volume maggiore; tra due poliedri regolari a facce simili inscritti in una stessa sfera, quello che ha il maggior numero di facce ha l'area e il volume maggiori. Egli pensava di poter stabilire la proprietà isoperimetrica come limite di una successione di aree di poliedri, cioè approssimare la sfera con la successione infinita dei poliedri ai quali è circoscritta. L'ostacolo è rappresentato dal fatto che le due proposizioni precedenti riguardano i poliedri regolari, e il numero di questi è finito.

Gran parte del trattato consiste nella dimostrazione delle due proposizioni. A questo scopo egli comincia con lo stabilire cinque lemmi (lemmi dal 6 al 10), che riguardano tutti disuguaglianze di rapporti tra angoli solidi e tra aree. È questa, a nostra conoscenza, la prima applicazione importante ed estensiva dell'angolo solido e quindi anche del primo considerevole studio di alcune sue proprietà. Mediante tali lemmi stabilisce, in tutta generalità, le due proposizioni precedenti. Queste si applicano però solo al tetraedro, all'ottaedro e all'icosaedro, in quanto il numero di facce di un poliedro regolare a facce quadrate o pentagonali è fisso (6 o 12). La prima proposizione significa dunque che se un tetraedro, un ottaedro e un icosaedro regolare hanno la stessa area, allora i loro volumi sono, nell'ordine detto, crescenti. La seconda, che se un tetraedro, un ottaedro e un icosaedro regolare sono inscritti in una medesima sfera, i loro volumi sono, nell'ordine detto, crescenti. Non si può pertanto approssimare la sfera con una successione infinita di poliedri regolari. Una tale inavvertenza da parte di un matematico che conosceva meglio di chiunque altro gli Elementi di Euclide è sconcertante. Come ha potuto non vedere che questi poliedri erano soltanto quelli di cui parla Euclide? Che il loro numero è finito? Una svista che non deve tuttavia offuscare la ricchezza del trattato. Fermiamoci per il momento alla dimostrazione delle due proposizioni.

L'idea della dimostrazione della prima proposizione si può riassumere nel modo seguente. Sia A (rispettivamente B) il centro della sfera circoscritta al primo (secondo) poliedro, AE (BG) la distanza del centro dal piano di una delle facce, S_A (S_B) l'area totale del poliedro e V_A(V_B) il volume, allora: V_A=(1/3)S_A∙AE e V_B=(1/3)S_B∙BG. Siano n_A e n_B il numero delle facce dei poliedri e supponiamo n_B>n_A.

Ibn al-Hayṯam dimostra allora che BG>AE e quindi che V_B>V_A. La dimostrazione consiste nel confrontare AE e BG. La riprendiamo qui per illustrarne il procedimento e lo stile. Consideriamo su EC un punto K tale che GH=EK e su ED un punto L tale che EL=GI. Se fosse AE=BG la piramide AEKL sarebbe uguale alla piramide BGHI e si avrebbe l'angolo solido (A, EKL) uguale all'angolo solido (B, GHI). Per il lemma 2 della prop. 4 sappiamo che

Se ne deduce, essendo S_A=S_B,

,

e si avrebbe dunque

,

ciò che, per il lemma 8, è assurdo. Dunque AE BG.

Se BG⟨AE, esiste M su AE tale che EM=BG, e si ha l'angolo solido (M, EKL) uguale all'angolo solido (B, GHI). Ma allora si avrebbe

(angoli al vertice di due triangoli isosceli aventi le stesse basi, rispettivamente KE, EL, KL), da cui:

,

e quindi si avrebbe l'angolo solido (M, EKL) maggiore dell'an golo solido (A, EKL). Per il lemma 8,

,

e pertanto qui si avrebbe

,

cioè:

,

e ciò per la [96] è assurdo. Si ha quindi necessariamente BG>AE, e di conseguenza V_B>V_A.

Per dimostrare la seconda proposizione, Ibn al-Hayṯam considera due poliedri regolari inscritti in una stessa sfera, di aree S1 e S2, volumi V1 e V2 e numeri di facce n1 e n2 tali che n1>n2. Se A è il centro della sfera circoscritta ai due poliedri, si avranno n1 piramidi regolari uguali di vertice A associate alle facce di P1 e n2 piramidi regolari uguali associate alle facce di P2.

Siano α1, s1 e h1 l'angolo al vertice, l'area di base e l'altezza di una piramide regolare P′1 associata a P1, e α2, s2 e h2 gli elementi di una piramide regolare P′2 associata a P2. Si ha n1α1=n2α2=4π, e poiché n1>n2 si ha α1⟨α2. Possiamo supporre che due piramidi P′1 e P′2 abbiano lo stesso asse AH; poiché α1⟨α2 l'angolo solido di P′1 è interno a quello di P′2, gli spigoli di P′1 incontrano la sfera al di là del piano di base di P′2. I piani delle due basi sono paralleli e tagliano la sfera secondo i cerchi circoscritti a queste basi; se ne deduce che s1⟨s2 e h1>h2. D'altra parte si ha:

da cui

Si è dimostrato (prop. 9) però che α2/α1>s2/s1, si ha dunque (s2/s1)(S1/S2)>s2/s1, da cui S1>S2. Sappiamo che V1=(1/3)S1h1 e V2=(1/3)S2h2, e poiché S1>S2 e h1>h2, si ha V1>V2. Questo teorema, anche se si dimostra in generale con il metodo di Ibn al-Hayṯam, si applica solamente al caso del tetraedro, dell'ottaedro e dell'icosaedro.

Egli dimostra poi il corollario seguente: siano P1 e P2 due poliedri regolari inscritti in una stessa sfera e aventi rispettivamente n1 e n2 facce e tali che le facce siano poligoni regolari aventi n′1 e n′2 lati; se n1>n2 e n′1>n′2, allora S1>S2 e V1>V2. Poiché i poliedri in questione sono regolari, questo corollario significa che se un tetraedro, un cubo e un dodecaedro regolari sono inscritti in una stessa sfera, le loro superfici laterali e i loro volumi sono, nell'ordine detto, crescenti. Abbiamo visto che il procedimento dinamico seguito da Ibn al-Hayṯam per risolvere il problema isoperimetrico nello spazio e pensato in qualche modo per analogia con quello seguito nel caso del piano, si scontra con il fatto che i poliedri regolari sono in numero finito.

Questo contributo di Ibn al-Hayṯam, e prima di lui quello di al-Ḫāzin, sono di gran lunga i più importanti della matematica araba. Nessun altro, a nostra conoscenza, li ha uguagliati. Le ricerche dei loro successori come, tra gli altri, Ibn Hūd, ǧĀbir ibn Aflaḥ, Abū 'l-Qāsim al-Sumaysāṭī non raggiungono il livello di quelle di al-Ḫāzin, e ancora meno di al-Hayṯam. Abbiamo sì Ibn Hūd che studia il problema isoperimetrico nel libro al-Istikmāl (Perfezionamento), ma non fa altro che riprendere la dimostrazione di Ibn al-Hayṯam, con qualche variante. Quanto ad al-Sumaysāṭī, non aggiunge nulla di essenziale ai risultati di al-Ḫāzin. ǧĀbir ibn Aflaḥ, l'astronomo di al-Andalus, nel suo Iṣlāḥ al-Maǧisṭī (La rettifica all'Almagesto) considera solo il caso dello spazio e nelle dimostrazioni solo i poliedri regolari. Molto probabilmente è dalla traduzione latina di quest'ultimo libro che Tommaso Bradwardine prende una proposizione del Libro II della sua Geometria speculativa, che si ritroverà più tardi in Cardano nel De subtilitate, e che afferma: tra tutte le figure piane isoperimetriche aventi lo stesso numero di lati e di angoli uguali, la più grande ha i lati uguali. Si tratta precisamente della prop. 6 di al-Ḫāzin.

Soltanto la ricerca storica futura potrà dirci se vi sono stati altri studi del livello di quelli di al-Ḫāzin e di Ibn al-Hayṯam, se il contributo di quest'ultimo è stato ripreso e sviluppato, e se parte di questo argomento è stato trasmesso ai matematici della latinità. Senza voler togliere ogni speranza, ci sembra però difficile che si sia andati oltre Ibn al-Hayṯam (le sue ricerche sull'angolo solido lo confermeranno) senza ulteriori mezzi analitici, ancora da inventare. Ma la nostra è solo una congettura.

La teoria dell'angolo solido

Nel corso delle ricerche sul problema isoperimetrico nello spazio, Ibn al-Hayṯam sviluppa una teoria dell'angolo solido. Si tratta della prima vera e propria teoria dell'angolo solido dopo quella, ben modesta, di Euclide, che non sarà uguagliata, e ancor meno superata, se non molti secoli dopo. Con essa, nell'XI sec., la ricerca archimedea in geometria si arricchirà di un nuovo capitolo. Per poter valutare pienamente il contributo di Ibn al-Hayṯam, occorre ripercorrere brevemente la storia degli studi sull'angolo solido prima di lui.

Il primo lavoro di cui abbiamo conoscenza è quello di Euclide negli Elementi. Nel Libro XI, nel quale viene dato inizio allo studio della geometria dei solidi, Euclide definisce l'angolo solido e ne elabora una teoria nelle propp. 20, 21, 22, 23 e 26, prima di applicarla nelle propp. 27, 36 e 37 dello stesso libro, e nello scolio del Libro XIII. Questa teoria, va detto subito, riguarda meno l'angolo solido che i rapporti tra gli angoli piani che lo formano. Il Libro XI comprende 28 definizioni. L'undicesima, relativa all'angolo solido, è la seguente: "Angolo solido è l'inclinazione [reciproca] di più di due linee che si tocchino tra loro, ma non siano sulla stessa superficie. O altrimenti: angolo solido è quello compreso da più di due angoli piani, che non siano nello stesso piano e abbiano in comune un punto [vertice]".

È chiaro che in questa doppia definizione, la prima, di angolo piano, è ricalcata sulla def. VIII del Libro I (un angolo piano è l'inclinazione reciproca di due rette che si incontrano in un piano e che non hanno la stessa direzione). È altrettanto chiaro che, presa alla lettera, questa definizione solleva molti problemi. Si pensi a un angolo solido formato dall'inclinazione di tre linee curve: queste, prese due a due, non formano un angolo piano perché non sono complanari. La seconda definizione sembra permettere a sua volta di parlare di una sola specie di angolo solido. Non è possibile in effetti parlare per esempio dell'angolo solido al vertice di un cono di rivoluzione. Comunque sia, questa doppia definizione ha fatto versare fiumi d'inchiostro e si è dubitato anche dell'autenticità della prima definizione (Heath 1926). La seconda definizione è stata accolta dalla tradizione araba degli Elementi, nelle varie copie della traduzione di I sḥāq-ṯĀbit, ed è questa definizione che riporta Ibn al-Hayṯam nel suo Kitāb fī ḥall šukūk kitāb Uqlīdis fī 'l-Uṣūl (Libro sulla risoluzione dei dubbi relativi agli Elementi di Euclide). Tuttavia, ritroviamo la prima definizione in un frammento che comprende il prologo del Libro XI, e la cui traduzione è attribuita esplicitamente al padre di Isḥāq, cioè a Ḥunayn ibn Isḥāq (questo frammento si trova intercalato su due fogli nel manoscritto Malik 3586 conservato a Teheran). Le cinque proposizioni che costituiscono la teoria dell'angolo solido di Euclide sono le seguenti. La prop. 20 afferma che, se un angolo solido è compreso da tre angoli piani, la somma di due qualunque di essi, in qualsiasi modo presi, è maggiore dell'angolo rimanente; la prop. 21, che ogni angolo solido è compreso da angoli piani la cui somma è minore di quattro angoli retti. A proposito di quest'ultima, Thomas Heath scrive giustamente: "Si osserverà che, anche se Euclide enuncia la proposizione per tutti gli angoli solidi, essa viene dimostrata soltanto nel caso particolare di un angolo triedro" (1926, III, p. 210). La dimostrazione di Euclide dipende dalla prop. 32 del Libro I e quindi dal postulato delle parallele, e sappiamo, dopo Nikolaj I. Lobačeskij e Bolyai, che la geometria sulla sfera non dipende dal postulato delle parallele.

L'enunciato della prop. 22 è il seguente: se vi sono tre ango li piani, e la somma di due di essi, in qualsiasi modo presi, è maggiore del rimanente, e tali angoli sono compresi tra rette, è possibile costruire un triangolo con le rette che congiungono gli estremi delle rette uguali. Questa proposizione è in realtà un lemma che serve a dimostrare la prop. 23 che è la principale di questo gruppo: con tre angoli piani, tali che la somma di due di essi, in qualsiasi modo presi, sia maggiore di quello rimanente, costruire un angolo solido; occorre dunque che la somma dei tre angoli sia minore di quattro retti. Infine, la prop. 26 è la seguente: su una retta data [come spigolo] e in un punto su essa [come vertice] costruire un ango lo solido uguale a un angolo solido dato.

Senza aver prima definito l'uguaglianza di due angoli solidi nel senso della misura, Euclide dimostra quest'ultima proposizione supponendo in realtà che due angoli triedri sono uguali: "Questa proposizione assume di nuovo l'uguaglianza di due angoli triedri che hanno i tre angoli piani di uno dei due rispettivamente uguali ai tre angoli piani dell'altro presi nello stesso ordine" (ibidem, p. 329). In altre parole, Euclide assume senza dimostrarlo che due angoli solidi triedri sono uguali se gli angoli piani che li formano sono a due a due uguali. Un'ipotesi implicita che tra l'altro non è sempre vera, come si vede considerando un angolo solido formato da quattro angoli piani: è possibile in questo caso formare con i quattro angoli piani dati infiniti angoli solidi diversi. Tuttavia, l'enunciato della prop. 26 è vero senza restrizioni. Lo scarto tra l'enunciato e la dimostrazione è un indizio: alla generalità dell'enunciato ‒ Euclide non specifica la natura dell'angolo solido ‒ si contrappone la dimostrazione limitata ai soli angoli solidi triedri, segno che negli Elementi Euclide tratta unicamente di questi ultimi. Non è tuttavia la sola restrizione. Abbiamo visto che Euclide si propone di stabilire l'uguaglianza di due angoli solidi senza però definire esplicitamente la nozione di uguaglianza. Ne segue che egli presuppone tacitamente che un angolo solido è una grandezza allo stesso titolo delle altre, come l'angolo piano per esempio. Ma non dà mai regole per trattare questa grandezza, per confrontare per esempio gli angoli solidi tra loro utilizzando l'angolo solido retto compreso da tre angoli piani retti. Questo confronto, anche se ci si limita ai triedri, è indipendente dalla somma degli angoli piani che definiscono l'angolo solido. Si cercherebbe perciò invano negli Elementi un qualunque studio dell'angolo solido come grandezza: la teoria dell'angolo solido resta estremamente povera.

Dopo Euclide, la storia dell'angolo solido non si arricchirà di nuovi elementi. La sola informazione proviene dalla seconda parte, dedicata ai corpi solidi, del Libro V della Collezione matematica. Pappo scrive a proposito dei tredici poliedri semiregolari:

Infatti, se per i poliedri nei quali gli angoli solidi sono compresi da tre angoli piani si contano semplicemente gli angoli piani alle basi del poliedro, è evidente che il numero degli angoli solidi è un terzo del numero ottenuto; mentre per i poliedri nei quali l'angolo solido è compreso da quattro angoli piani, se si contano tutti gli angoli alle basi del poliedro, il numero degli angoli solidi di questo poliedro è un quarto del numero ottenuto. Infine, analogamente per i poliedri nei quali l'angolo solido è compreso da cinque angoli piani, il numero che esprime la quantità degli angoli solidi è un quinto della quantità degli angoli piani. (I, p. 274)

Si tratta, come ricorda Pappo, dei tredici poliedri scoperti da Archimede nel libro andato perduto. Così, dopo Euclide, l'angolo solido viene almeno ricordato da Archimede nelle sue ricerche sui poliedri semiregolari. Ma poiché non conosciamo questo scritto del matematico di Siracusa, quello che sappiamo si ferma qui. Questo è, a quanto sembra, lo stato delle ricerche sull'angolo solido fino alla ripresa del IX secolo. La storia degli studi sull'angolo solido non è ancora stata scritta, ma possiamo affermare che a partire da quel momento la ricerca prende due direzioni. La prima si basa sul Libro XI degli Elementi e si propone di migliorare la dimostrazione di Euclide; la seconda è direttamente legata all'approssimazione di un corpo convesso con poliedri. Come esempio dei lavori nella prima direzione citiamo quelli di al-Siǧzī e di Ibn al-Hayṯam, ma ve ne saranno probabilmente altri, mentre l'altra direzione è seguita da Ibn al-Hayṯam.

Il primo matematico che si sia interessato all'angolo solido è, per quanto ne sappiamo, Aḥmad ibn ῾Abd al-ǧalīl al-Siǧzī (seconda metà del X sec.). Egli ritorna almeno due volte sull'angolo solido. In un libro dal titolo al-Madḫal ilā ῾ilm al-handasa (Introduzione alla scienza della geometria), egli procede a una classificazione dei differenti tipi di angolo solido: "uno è quello compreso da una sola superficie, il secondo quello compreso da una superficie e da un piano, e il terzo da due piani" (Dublino, Chester Beatty, 3652, f. 8). Gli esempi che presenta sono: per il primo tipo, l'angolo al vertice di un cono di rivoluzione o quello a uno dei vertici di un ellissoide; per il secondo, un semicono di rivoluzione; per il terzo tipo, l'angolo compreso da tre piani ‒ il triedro ‒ nel quale la somma è minore di quattro angoli retti. In un altro scritto, Risāla fī ḥall al-šakk allaḏī fī 'l-šakl al-ṯāliṯ wa-'l-῾išrīn min al-maqāla al-ḥādiyya ῾ašara min kitāb Uqlīdis (Trattato sul chiarimento del dubbio concernente la prop. 23 del Libro XI di Euclide), egli riprende il lemma e la proposizione di Euclide. Nell'introduzione si rivolge ad altri matematici che avevano sollevato dubbi sulla dimostrazione di Euclide. Come dire che all'epoca al-Siǧzī non era il solo a preoccuparsi dell'angolo solido, almeno nell'ambito euclideo.

Il secondo matematico è Ibn al-Hayṯam stesso. Anche lui riprende la dimostrazione di Euclide per correggerla nel Kitāb fī ḥall šukūk kitāb Uqlīdis fī 'l-Uṣūl. Interessanti sia per la storia del Libro XI degli Elementi in arabo che per quella dell'angolo solido, questi studi non cambiano tuttavia radicalmente la natura della teoria euclidea.

Il terzo studio, di gran lunga il più innovativo e il più importante, è quello di Ibn al-Hayṯam nel libro sugli isoperimetri nel piano e nello spazio. È in questo testo che egli elabora una teoria dell'angolo solido. In quale modo è arrivato a questa teoria? Come abbiamo visto, uno degli scopi che qui si prefigge è quello di dimostrare la proprietà massimale della sfera. Seguendo i suoi predecessori, come al-Ḫāzin, egli opta per una strategia di tipo infinitesimale, cioè un procedimento che consiste nell'approssimare il volume della sfera con una successione di volumi di poliedri convessi. La scelta infelice dei poliedri regolari non modifica l'intenzione che presiede alla scelta di questa strategia, che richiede però che si possano confrontare i volumi di poliedri convessi. Ora, un tale confronto è evidentemente più semplice se si passa per l'angolo solido, e di conseguenza se si confrontano gli angoli solidi. Ma il confronto si può fare solo tra grandezze e per mezzo di grandezze. Bisognava perciò concepire esplicitamente l'angolo solido come una grandezza, e soggetto quindi alle operazioni che si applicano alle grandezze e alla teoria delle proporzioni. Egli stabilisce poi numerosi lemmi sull'angolo solido: lo scopo è dimostrare la proprietà estremale, ma questi lemmi costituiscono i teoremi di una nuova teoria dell'angolo solido. Che procedimento ha seguito per stabilire questa teoria?

In una tale situazione la via più naturale da percorrere, anche se non facile, è quella dell'analogia: partire dalla teoria dell'angolo piano e generalizzarla allo spazio. Ma non bisogna lasciarsi trarre in inganno: questa analogia ha tutt'al più un valore euristico; il passaggio allo spazio non è semplice e presenta molte insidie. E infatti molte proprietà che valgono nel caso dell'angolo piano non sussistono più per l'angolo solido. La conoscenza dei rapporti tra corde e angoli al centro che le intercettano nella circonferenza fornirà a Ibn al-Hayṯam alcune intuizioni notevoli, ma nulla per quanto riguarda i concetti della teoria dell'angolo solido. Egli si trova dunque in una situazione che non è uguale ad alcun'altra, in quanto si pone per così dire nella prospettiva della geometria archimedea con gli strumenti della geometria sferica; siamo ben lontani dal quadro euclideo. Per illustrare tutto ciò veniamo agli elementi di questa teoria.

Ibn al-Hayṯam comincia con il richiamare un risultato di Archimede, che egli dimostra di nuovo nel trattato Qawl fī misāḥat al-kura: il volume della sfera di raggio r è 4/3πr3. Ibn al-Hayṯam scrive poi:

Ogni poliedro regolare inscritto nella sfera è tale che se si conducono dal centro della sfera dei piani passanti per i lati di una delle sue basi questi piani separano dalla sfera un settore il cui rapporto con l'intera sfera è uguale al rapporto tra la superficie sferica base del settore e la superficie totale della sfera, ed è uguale al rapporto tra l'angolo solido ‒ che si trova al centro della sfera e limitato dalle superfici della piramide regolare le cui linee sono rette e la cui base è una della basi del poliedro ‒ e gli otto angoli solidi retti somma di tutti gli angoli solidi al centro della sfera e che sono al centro di tutti i poliedri regolari in quanto la sfera e la sua superficie sono divise da questi piani in parti uguali. (Rashed 1993a, pp. 401-402)

In questo passo egli introduce la nozione di angolo solido nelle sue relazioni con superfici sferiche e sezioni sferiche. Più precisamente, se A è l'area della sfera, s l'area della superficie sferica relativa alla sezione, v il volume della sezione sferica, V il volume della sfera, α l'angolo solido, D l'angolo solido retto, si ha

e i rapporti sono uguali a 1/n, dove n è il numero di facce del poliedro. Solo in seguito definisce e costruisce l'angolo solido retto:

Se si prende un cerchio massimo della sfera, si tracciano due diametri che si intersecano ad angolo retto, si traccia dal centro una perpendicolare al piano del cerchio e la si prolunga da entrambi i lati, si tracciano dalle due estremità di questa delle rette [perpendicolari] agli estremi dei due diametri, si formano nella sfera otto piramidi uguali con i vertici al centro della sfera e gli angoli al vertice uguali. Ciascuno di questi angoli è detto 'angolo solido retto' e la somma di questi angoli è la somma degli angoli di ogni poliedro inscritto nella sfera. (ibidem, p. 402)

Deduce allora che v=(1/3)sr. Si osserva già che qui non opta per la definizione euclidea dell'angolo solido. Prende infatti le mosse da un poliedro regolare inscritto in una sfera. A ogni faccia del poliedro associa una piramide regolare il cui vertice è il centro B della sfera. Definisce mediante la [104] un angolo solido di vertice B, una superficie sferica e una sezione della sfera. Dimostra poi sei proposizioni. La prop. 1 è la seguente. Sia A il centro di una sfera, e consideriamo due piramidi P1(ABCDE) e P2(AHFG). La piramide P1 di angolo solido α1 intercetta una superficie sferica s1 e delimita una sezione sferica di volume v1. Analogamente, a P2 si associano α2, s2 e v2. Si ha

A n volte la piramide P1 vengono associati la parte della sfera di volume nv1, la superficie sferica intercettata ns1 e l'angolo solido nα1 e lo stesso per P2.

Se nv1>nv2, allora nα1>nα2 e ns1>ns2;

se nv1⟨nv2, allora nα1⟨nα2 e ns1⟨ns2;

se nv1=nv2, allora nα1=nα2 e ns1=ns2;

se nα1>nα2, allora ns1>ns2 e nv1>nv2;

se nα1⟨nα2, allora ns1⟨ns2 e nv1⟨nv2;

e se nα1=nα2, allora ns1=ns2 e nv1=nv2.

Osserviamo che le spiegazioni date da Ibn al-Hayṯam non costituiscono una dimostrazione della proprietà annunciata [105]. La prop. 2 afferma che, se ABCD è una piramide tale che

e se E è un punto di BD tale che

,

allora

Sia ∑ una sfera di centro A e di raggio AB che interseca AC in H, AD in I, AE in L, tali che AB=AH=AI=AL. Si ha dunque nel piano (BAC) l'arco BH, nel piano (BAD) l'arco BLI, nel piano (ACD) l'arco HI e nel piano (ACE) l'arco HGL. La ret ta BL si trova nel piano (BAD), interseca AD in K (in quanto

è acuto e

pure). L'arco LGH è su ∑, e dunque K è all'esterno di ∑, con AK>AI. La superficie conica di vertice B definita dall'arco LGH taglia il piano (ADC) secondo un arco KFH, in quanto ogni retta BG taglia questo piano in F all'esterno della sfera ∑; l'arco KFH, escluso H, è all'esterno di ∑. Allora la sezione della sfera AILGH è all'interno del solido AKFHGL, limitato da piani e da una parte della superficie conica, in quanto la parte GF della generatrice è all'esterno di ∑ e la sezione ALHB della sfera è maggiore del solido ALHB, limitato da piani e da un'altra parte della superficie conica, in quanto il segmento di generatrice BG del cono è all'interno di ∑.

Per composizione si ha

Nel corso della dimostrazione di questa prop. 2 Ibn al-Hayṯam introduce un'altra proposizione il cui enunciato è:

in altri termini si tratta di dimostrare che la proiezione conica di centro B del piano AEC sul piano ADC aumenta alcuni rapporti di aree stellate rispetto ad A. La dimostrazione consiste nel ricondursi, per mezzo di una riduzione all'assurdo, al caso in cui si confrontano aree di triangoli di vertice A. Riprendiamo i passi di questa dimostrazione. Supponiamo che

esiste un'area L_a (quarto proporzionale) tale che

L'ipotesi [110] si scrive allora L_a>area settore (ALGH), ed esiste dunque un poligono LSQH circoscritto all'arco di cerchio LGH tale che

Egli considera il caso nel quale questo poligono ha tre lati LS, SQ, QH tangenti all'arco di cerchio nei punti L, G e H, rispettivamente. Il poligono LSQH viene proiettato nel piano ADC secondo il poligono KRPH i cui lati KR, RP, PH sono tangenti in K, F e H, rispettivamente, alla proiezione KFH (arco di conica) dell'arco di cerchio LGH.

Osserviamo che Ibn al-Hayṯam è perfettamente conscio del fatto che la proiezione conica conserva il contatto, ciò che ri corda le proprietà del piano tangente al cono note a Ibn Sahl. Si riduce allora l'enunciato alla disuguaglianza

Infatti il secondo rapporto di [113] è (secondo la [112]) maggiore del rapporto:

,

e quindi da [111] segue che

,

che è assurdo perché il poligono è circoscritto all'arco di cur va. Ibn al-Hayṯam afferma allora che la disuguaglianza [113] risulta dalle disuguaglianze

Purtroppo l'ultima affermazione non è sempre vera. Tuttavia, la proposizione è vera quando i punti C e D si trovano dalla stessa parte del piano perpendicolare ad ABD e passante per AB, una condizione sfuggita a Ibn al-Hayṯam ma che non inficierà le proposizioni successive che da essa dipendono. Ibn al-Hayṯam si mette sempre nelle condizioni favorevoli.

La prop. 3 afferma che, data una piramide ABCD tale che AB sia perpendicolare al piano (BCD) e

se E è un punto di CD, si ha:

Nel piano ABE tracciamo la perpendicolare in E ad AE. Essa taglia AB in G. Poiché

si ha BE>BC, e poiché AB è perpendicolare al piano (BCD) si ha AE>AC. Se si prolunga BC fino a E′ tale che BE′=BE, si ha

da cui

è ottuso.

Dimostriamo che

Nel caso

si ha CB perpendicolare a CD; ma CD è orto gonale ad AB, e dunque CD è perpendicolare al piano (ABC), e di conseguenza CD è perpendicolare ad AC, cioè

Nel caso

si può tracciare CD′ all'interno di

tale che CD′ sia perpendicolare a BC, allora CD′ è perpendicola re al piano (ABC) e AC è ortogonale a CD′, e dunque

e D′ è interno a BD.

Nel piano ACG si può tracciare CG′ perpendicolarmente ad AC, con G′ in BG. Allora il piano CD′G′ è perpendicolare ad AC e taglia il piano ABD secondo la retta G′D′ che incontra AD tra A e D in D″, e si ha

e dunque

Allora la piramide AGCD soddisfa le condizioni della prop. 2. Nel caso in cui

è retto, abbiamo visto che la proposizione non è sempre vera, ma il lemma resta vero.

Ibn al-Hayṯam prosegue il ragionamento in questo modo:

ma

e inoltre l'angolo solido (A, GCD) è uguale all'angolo solido (A, BCD) e l'angolo solido (A, GCE) è uguale all'angolo solido (A, BCE), da cui il risultato:

La prop. 4 afferma che, data una piramide ABCD tale che AB sia perpendicolare al piano (CBD) e che BC=BD; se EG è parallela a CD, allora:

Poiché EG è parallelo a CD, il triangolo BGE è isoscele. Se I è il punto di mezzo di EG, allora BI è perpendicolare a EG e taglia DC in H, punto di mezzo di CD. Ora, da AB ortogo nale a (CBD) segue che (ABC) è ortogonale a (CBD) e (ABH) è ortogonale a (CBD). Ma BH è l'intersezione di (ABH) e (BCD), e la retta GI del piano (BCD) è perpendicolare a BH; dunque è perpendicolare al piano (ABH), per cui

e analogamente

Sappiamo che

sono ottusi e che

possiamo applicare la prop. 2 con l'angolo

ottuso; è ancora il caso dubbio ma che resta vero perché i punti C e H sono dalla stessa parte del piano perpendicolare ad ABH passante per AB (CH è parallelo a questo piano):

La stessa prop. 2, con l'angolo AIG retto (vero in tutti i casi, l'angolo AIG ha il ruolo dell'angolo ACE della prop. 2) dà:

Moltiplicando membro a membro si ha

Se ne deduce, moltiplicando per 2 i membri del rapporto,

un calcolo integrale diretto permetterebbe d'altra parte di dimostrare questo lemma indipendentemente dalla prop. 2. La prop. 5 si riferisce a due piramidi regolari P₁ e P₂ di vertice A, le cui basi sono poligoni regolari simili ma diversi, inscritti in una sfera di centro A. Sia P₁ la piramide avente la base più grande e P₂ l'altra piramide; si ha:

L'idea fondamentale della dimostrazione, qui come altrove, è prendere come misura dell'angolo solido l'area della superficie sferica che esso intercetta. Infine, secondo la prop. 6, date due piramidi regolari P₁ e P₂ di vertice A aventi rispettivamente n₁ e n₂ facce, e le cui basi sono poligoni regolari B₁ e B₂ inscritti in una medesima sfera di centro A e di aree s₁ ed s₂, se n₁>n₂ e s₁⟨s₂ allora

Sono questi gli elementi che Ibn al-Hayṯam concepisce per una teoria dell'angolo solido. Come abbiamo osservato, i principî unificanti di questa teoria sono l'idea secondo la quale l'angolo solido è una grandezza allo stesso titolo delle altre grandezze geometriche, e quindi questa grandezza si può misurare con l'area della superficie sferica che essa intercetta, ciò permette di definire i rapporti tra poligoni piani inscritti in una sfera e angoli solidi al centro intercettando questi poligoni. A questo punto l'analogia con la teoria dell'angolo piano cessa di sussistere.

L'esame delle dimostrazioni delle proprietà precedenti mostra che Ibn al-Hayṯam combina proiezioni coniche e procedimenti di tipo infinitesimale. Si tratta dunque di uno dei capitoli più avanzati e sofisticati dell'epoca. Sembra che le cose si siano fermate a questo punto per sei secoli, fino alla comparsa dei Progymnasmata de solidorum elementis di Descartes e de La doctrine de l'angle solide di Florimond de Beaune. Quest'ultimo segue una strada sua propria, di contro Descartes manipola nozioni vicine a quelle di Ibn al-Hayṯam. Solo con Euler e con l'abate de Gua la teoria si trasformerà grazie all'intervento del calcolo differenziale e integrale.

Bibliografia

Becker 1936: Becker, Oskar, Zur Textgestaltung des eudemischen Berichts über die Quadratur der Möndchen durch Hippokrates von Chios, "Quellen und Studien zur Geschichte der Mathematik", 3, 1936, pp. 400-419.

‒ 1964: Becker, Oskar, Grundlagen der Mathematik, Freiburg-München, Alber, 1964.

Clagett 1964-84: Archimedes in the Middle Ages, edited by Marshall Clagett, v. I: The Arabo-Latin tradition, Madison, University of Wisconsin Press, 1964; v. V: Quasi-archimedean geometry in the thirteenth century, Philadelphia, American Philosophical Society, 1984.

Coolidge 1940: Coolidge, Julian L., History of geometrical methods, Oxford, Oxford University Press, 1940 (rist.: New York, Dover, 1963).

Heath 1926: Heath, Thomas L., The thirteen books of Euclid's Elements, 2. ed., Cambridge, Cambridge University Press, 1926, 3 v. (rist.: New York, Dover, 1956).

Mogenet 1961: Mogenet, Joseph, L'histoire des isopérimètres chez les Grecs, "Scrinium lovaniense. Mélanges historiques", 24, 1961, pp. 69-78.

Rashed 1991: Rashed, Roshdi, L'analyse et la synthèse selon Ibn al-Haytham, in: Mathématiques et philosophie de l'antiquité à l'âge classique. Hommage à Jules Vuillemin, sous la direction de Roshdi Rashed, Paris, CNRS, 1991, pp. 131-162 (trad. ingl.: Analysis and synthesis according to Ibn al-Haytham, in: Artifacts, representations and social practice. Essays for Marx Wartofsky, edited by Carol C. Gould and Robert S. Cohen, Dordrecht, Kluwer, 1994, pp. 121-140).

‒ 1993a: Rashed, Roshdi, Math. inf. II.

‒ 1993b: Rashed, Roshdi, Al-Kindi's commentary on Archimedes' 'The measurement of the circle', "Arabic sciences and philosophy", 3, 1993, pp. 7-53.

‒ 1993c: Rashed, Roshdi, Géométrie et dioptrique: Ibn Sahl, al-Qūhī et Ibn al-Haytham, Paris, Les Belles Lettres, 1993.

‒ 1996a: Rashed, Roshdi, Math. inf. I.

‒ 1996b: Rashed, Roshdi, Archimedean learning in the middle ages: the Banū Mūsā, "Historia scientiarium", 6, 1996, 1, pp. 1-16.

‒ 2000a: Rashed, Roshdi - Bellosta, Hélène, Ibrāhīm ibn Sinān. Logique et géométrie au X^e siècle, Leiden, E.J. Brill, 2000.

‒ 2000b: Rashed, Roshdi, Math. inf. III.

‒ 2002: Rashed, Roshdi, Math. inf. IV.

Rome 1936: Commentaires de Pappus et de Théon d'Alexandrie sur l'Almageste, texte établi et annoté par Adolphe Rome, Roma, Biblioteca Apostolica Vaticana, 1931-1943, 3 v.; v. II, 1936.

Schmidt 1901: Schmidt, Wilhelm von, Zur Geschichte der Isoperimetrie im Altertume, "Bibliotheca mathematica", 2, 1901, pp. 5-8.

Suter 1899: Suter, Heinrich, Die Kreisquadratur des Ibn al-Haitam, "Zeitschrift für Mathematik und Physik. Historisch-literarische Abteilung", 44, 1899, pp. 33-47.

Youschkevitch 1976: Youschkevitch, Adolf P., Les mathématiques arabes (VIII^e-XV^e siècles), trad. franc. de Michel Cazenave et Khalil Jaouiche, préface de René Taton, Paris, Vrin, 1976.