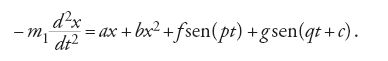L'Ottocento: fisica. L'acustica

L'Ottocento: fisica. L'acustica

L'acustica

Acustica fisiologica: Helmholtz

di Dieter Ullmann

Hermann von Helmholtz (1821-1894), uno dei massimi scienziati del XIX sec., dopo avere completato gli studi liceali a Potsdam, iniziò nel 1838 quelli di medicina presso l'Istituto per la formazione dei medici militari a Berlino, che nel 1825 era stato parificato agli istituti universitari medici civili. Tra i suoi professori un ruolo particolarmente importante rivestì il medico e fisiologo Johannes Peter Müller (1801-1858), figura decisiva in quello che sarebbe stato il futuro ambito di ricerca di Helmholtz. Müller aveva infatti aperto un'epoca nuova nel campo della fisiologia con il suo capolavoro, Handbuch der Physiologie des Menschen (Manuale di fisiologia umana, 1833-1840), pubblicato a Coblenza, caratterizzato dal forte legame con le altre scienze naturali. Gli allievi di Müller avevano una vasta preparazione nel campo della fisica; Heinrich Wilhelm Dove (1803-1879), per esempio, fisico berlinese particolarmente interessato all'acustica, indirizzava verso tale settore di ricerca i medici agli esordi. Dopo avere conseguito il diploma di laurea nel 1842 con Müller, Helmholtz lavorò come medico militare a Berlino e a Potsdam. Nella fisica, intanto, cominciavano a comparire i primi lavori sulle manifestazioni fisiologiche legate al calore e alla conservazione dell'energia. Nel 1849 Helmholtz venne chiamato a ricoprire la cattedra di fisiologia dell'Università di Königsberg (oggi Kaliningrad), nel 1855 all'Università di Bonn e nel 1858 presso l'Università di Heidelberg, dove rimase fino al suo trasferimento a Berlino nel 1871; il suo interesse per l'acustica risale al 1855.

Il primo lavoro di Helmholtz in questo campo riguardò lo studio dei toni di combinazione (1856). I toni differenza, che si hanno quando due toni ‒ o suoni che dir si voglia ‒ con frequenze p e q sono in accordo e presentano ognuno elevata intensità, erano ben noti da molto tempo a musicisti e costruttori di organi. Essi sono spesso chiamati 'toni di Tartini', in quanto citati da Giuseppe Tartini nel suo Trattato di musica secondo la vera scienza dell'armonia, pubblicato a Padova nel 1754 (l'autore li aveva tuttavia già individuati nel 1714). Lo studioso di acustica e teorico della musica Jean-Baptiste Romieu aveva fornito nel 1752 una spiegazione fisica del fenomeno del tono differenza p−q nelle condizioni sopra esposte, resa nota però solamente grazie al lavoro di Joseph-Louis Lagrange nel 1759 e, nei decenni successivi, generalmente accettata. Questa teoria si basa sui battimenti tra i due toni con frequenze p e q e uguale ampiezza A:

[1] ξ₁=Asen[2πp(t-x/v)], ξ₂=Asen[2πq(t-x/v)],

dove v è la velocità del suono e x la direzione di propagazione.

La sovrapposizione delle due onde si verifica nel punto x=0:

[2] ξ=ξ₁+ξ₂=2Acos{2π[(p-q)/2]t}sen{2π[(p+q)/2]t}.

Se ∣p−q∣≪p+q, allora si sente una vibrazione di frequenza media (p+q)/2≈p≈q con ampiezza 2Acos{2π[(p−q)/2]t} che cambia lentamente. Se il numero dei battimenti o colpi a unità di tempo scende al di sotto della soglia di udibilità, essi non vengono più percepiti distintamente ma si mescolano in un tono, il tono differenza osservato.

Thomas Young aveva scoperto nel 1800 i toni differenza di secondo ordine e Gustav Gabriel Hällström ne aveva identificati alcuni di ordine superiore: era dunque divenuto possibile affermare che, in caso di presenza contemporanea di due toni di elevata intensità di frequenze p e q, era possibile udire i seguenti toni differenza:

[3] f=∣np-n'q∣,  n, n'=1, 2, 3,…,

laddove il caso di n=n′=1 rappresenta il tono differenza di primo ordine. Si poteva parlare perciò anche di toni di combinazione.

Georg Simon Ohm (1787-1854), prima ancora della sua importante pubblicazione del 1843, già nel 1839 aveva scritto un breve saggio di acustica sui toni di combinazione e sui risultati ottenuti da Hällström. I due toni generatori del tono differenza di primo ordine dovevano, secondo Ohm, avere la forma sinusoidale [1], per cui, in caso di sovrapposizione, si produceva un'equazione della forma [2]. Per Ohm, tuttavia, ciò significava nello stesso tempo che il tono differenza del primo ordine e uno dei toni primari non potevano essere insieme i fattori responsabili della generazione di un tono differenza di secondo ordine ‒ come invece affermava Hällström ‒ perché la [2] non è più un tono primario come la [1], ossia non è un tono ohmico. Ohm propose di spiegare i toni differenza di ordine più alto mettendoli in correlazione con le armoniche superiori che accompagnano la tonica, ossia la frequenza fondamentale della scala musicale di interesse. Tale spiegazione sarebbe stata però valida solamente per i toni di strumenti musicali che dispongono di toni armonici superiori, come gli strumenti a fiato e a corda; nel caso, per esempio, di un diapason nel quale i suoni armonici superiori non siano armonici con la tonica, questa spiegazione non era soddisfacente. Da questo punto presero avvio i lavori di Helmholtz, che condussero alla pubblicazione della sua fondamentale opera Über Combinationstöne (Sui toni di combinazione, 1856). Secondo Helmholtz, i battimenti non potevano essere la causa della generazione di toni di combinazione, per il semplice fatto che la [2] non è più un tono nel senso di Ohm.

Helmholtz sottolineava la necessità di disporre per le sue ricerche di toni privi di armoniche superiori. A tale scopo egli utilizzò in particolare l'effetto di cavità risonanti; questi risonatori, detti di Helmholtz, svolsero a partire da quel momento un ruolo importante nell'acustica sperimentale. Posizionando un diapason davanti all'imboccatura di un risonatore idoneo, il tono fondamentale aumenta di molto ma non si verifica nessun rafforzamento dei toni armonici superiori.

Helmholtz di conseguenza scoprì che, oltre ai toni differenza, esistono anche toni somma, sensibilmente più deboli, e che entrambi i fenomeni erano compresi sotto il termine di toni di combinazione. I battimenti quali causa dei toni di combinazione ‒ come ritenevano Romieu e Lagrange ‒ non soltanto non sono toni nel senso di Ohm ma neanche produrrebbero toni somma.

Queste riflessioni mi hanno portato a notare l'insufficienza delle teorie sinora avanzate e ho creduto di scoprire un'indicazione che poteva condurre sulla strada giusta nel fatto, sino a questo momento scarsamente rilevato, che i toni di combinazione compaiono soltanto nel caso di toniche forti e che la loro intensità sembra aumentare in un rapporto assai più rapido di quella dei toni primari. Di conseguenza ho creduto di poter ipotizzare che essi non possano formarsi in caso di lunghezze d'onda di ampiezza infinitamente piccola ‒ come, in teoria, sono normalmente considerate quelle sonore ‒ ma solo nel caso di lunghezze d'onda di ampiezza finita. (Helmholtz 1856, p. 531)

Per semplificare, Helmholtz trattò nella propria teoria soltanto la vibrazione di un singolo punto di materia di massa m₁ in direzione x, laddove per la forza elastica egli formulò l'equazione:

[4] k=ax+bx².

Se ora sul punto di materia agiscono due treni di onde sonore con forze fsen(pt) e gsen(qt+c), per l'equazione del moto si ha l'equazione

Helmholtz integrò la [5] esprimendo la x come serie di potenze

[6] x=εx₁+ε²x₂+ε³x₃+…,

con f=εf₁ e g=εg₁, ponendo uguali a zero i termini con le stesse potenze di ε; x₂ contiene i toni con frequenze 2p, 2q, p−q e p+q; x₃ contiene quelli con frequenze 3p, 3q, 2p+q, 2p−q, p+2q, p−2q, p e q; x₄ produce i toni di combinazione di terzo ordine, eccetera. Se dunque, in base alla teoria di Helmholtz si ammette che, in caso di vibrazioni della membrana del timpano, il quadrato delle elongazioni produca un effetto sulle oscillazioni stesse, è possibile spiegare la formazione dei toni di combinazione. Si accenna inoltre al fatto che nell'equazione [4], cambiando il segno di x si produce una variazione di ∣k∣. L'equazione è dunque adatta a descrivere un corpo elastico che, rispetto a spostamenti in direzione x positiva o negativa, non si comporti in maniera simmetrica. Helmholtz sottolineò che un'asimmetria caratterizza in particolare la membrana del timpano dell'orecchio, che attraverso il martello viene fortemente tirata in dentro.

Nella sua famosa teoria della risonanza (1869), Helmholtz partì dall'idea che la membrana basilare può essere considerata come un sistema di risonatori in forma di fibre tese trasversali di diversa frequenza propria. In conseguenza dello smorzamento attuato dalle fibre, un gruppo abbastanza ampio di esse viene stimolato a vibrare insieme mediante un tono. Ciò spiega, in effetti, per quale motivo, sentendo contemporaneamente due toni molto vicini, si percepisca una sola vibrazione ‒ il già citato battimento ‒ ma non chiarisce in che modo, in base alla vecchia teoria dei battimenti per i toni differenza (secondo Romieu e Lagrange al di là del limite della distinzione delle frequenze, ossia per un ampio intervallo di toniche) si possa sentire un solo tono differenza. In questo caso entrambi i gruppi in risonanza sulla membrana basilare risultano infatti sufficientemente lontani l'uno dall'altro. Su questo punto la teoria di Helmholtz sembra dunque in vantaggio. La teoria dei battimenti, inoltre, non spiega i toni somma, benché la loro esistenza venga in vario modo messa in dubbio. Il tono somma di primo ordine p+q, quindi, può (formalmente) essere concepito come tono differenza tra il primo tono armonico superiore di p e il tono differenza di primo ordine p−q.

A fronte dei suoi vantaggi, la teoria presenta dei difetti. Il tono differenza p−q è, per Helmholtz, soltanto un effetto di secondo ordine. Alcuni esperimenti hanno però dimostrato che questo tono può avere per brevi intervalli un'intensità rilevante; esso è particolarmente intenso solo fino alla quinta, perché in caso di intervalli più lunghi, i toni di combinazione diventano assai deboli. Tale fenomeno non è comprensibile in base alla teoria di Helmholtz. Per l'intensità dei toni di combinazione risulta determinante anche il rapporto delle intensità, mentre secondo Helmholtz conta solamente il prodotto delle ampiezze. Esperimenti hanno inoltre mostrato che, nei registri di frequenza più alti dei toni primari, il tono differenza p−q è più forte che nei registri più bassi; anche questa è un'osservazione che la teoria di Helmholtz non consente di desumere.

All'ulteriore progresso nella comprensione dei toni di combinazione si lega in particolare il nome di Erich Waetzmann (1882-1938), il quale, all'inizio del XX sec., svolse presso la Technische Hochschule di Breslavia (l'odierna Cracovia) approfondite indagini su questo argomento. Oggi è noto, inoltre, che non si deve alla membrana del timpano la formazione dei toni di combinazione, i quali sono invece il risultato di una distorsione non lineare del segnale acustico nella coclea.

Nell'opera Die Akustik di Ernst Florens Friedrich Chladni (1756-1827) i concetti di consonanza e dissonanza sono ancora spiegati come era consueto da secoli: "Un intervallo è consonante quando i numeri delle vibrazioni sono tra loro in un rapporto tanto semplice che l'udito le afferra nel modo più facile e ne viene così tranquillizzato; per contro, un intervallo è dissonante quando i numeri delle vibrazioni si trovano in una relazione meno semplice […]" (Chladni 1802, p. 8). L'autore indica anche che gli intervalli consonanti sono quelli caratterizzati dai numeri da 1 a 6, mentre il 7 segna il passaggio alla dissonanza.

La teoria dei toni di combinazione di Helmholtz svolge un ruolo anche nella sua teoria della consonanza, secondo la quale il grado di dissonanza dipende dalla forza della ruvidezza prodotta mediante il battimento dei toni armonici superiori di entrambi i timbri che colpiscono l'orecchio. Se i due timbri coincidono esattamente in tutti i toni armonici superiori, i battimenti scompaiono e si crea un intervallo consonante in maniera ideale. Si pone però la questione di quali siano i rapporti nel caso dei toni privi di armoniche superiori, che produrrebbero battimenti solamente per intervalli di toni brevi. Per intervalli di toni puri più ampi questa spiegazione sarebbe insufficiente a distinguere consonanza e dissonanza. Secondo Helmholtz i battimenti dei loro toni di combinazione sono in questo caso responsabili della consonanza e della dissonanza. Il fenomeno si produce, per esempio, nel caso delle ampie canne d'organo chiuse, che hanno solo toni semplici. Soltanto gli intervalli stretti di seconda producono battimenti energici, mentre intervalli più ampi impuri producono esclusivamente i battimenti deboli del primo tono differenza. Gli intervalli dissonanti (con l'eccezione di quello di seconda) si distinguono dunque poco da quelli consonanti.

Il tema della consonanza e dissonanza è stato sviluppato ulteriormente in seguito. In merito alla teoria della fusione dei toni, dopo quella del 1898 dello psicologo e studioso di musica Carl Stumpf, il quale riteneva che la differenza tra consonanza e dissonanza fosse di tipo quantitativo e non qualitativo, si arriva alla concezione attuale, secondo cui la consonanza si deve al meccanismo di riconoscimento di modelli di sollecitazione spaziale sulla membrana basilare.

Nel 1857 Helmholtz iniziò i suoi studi sulle vocali. Egli descrisse un semplice esperimento: inserì la sordina a un pianoforte ben accordato e cantò le vocali con forza verso la cassa armonica, producendo la risonanza delle corde musicali corrispondenti alle armoniche delle singole vocali. Indicando con 1 la tonica e con 2, 3, e così via, le armoniche superiori si otteneva il seguente risultato: nel caso della A spiccano accanto a 1 le armoniche 3 e 5 mentre 2, 4 e 7 sono più deboli; nel caso della O, 3 è debole e molto deboli sono 2 e 5; nel caso della U domina la tonica, accompagnata dall'armonica debole 3; per la E è molto forte 2 e le armoniche più alte si percepiscono appena; per la I sono importanti 2 e 3 mentre 1 e 5 sono deboli.

I metodi di ricerca furono affinati e, secondo Helmholtz, "[…] le vocali della voce umana sono generate da ance costituite da una membrana, vale a dire le corde vocali, il cui tubo sonoro addizionale, la cavità orale, può contenere diverse ampiezze, altezze e intonazioni, in maniera tale da rinforzare ora l'uno, ora l'altro tono parziale del timbro" (Helmholtz 1863 [1913, p. 168]).

Tenendo diversi diapason davanti alla bocca aperta si otteneva un rafforzamento del tono del diapason, quanto più precisamente esso corrispondeva a uno dei toni propri della massa d'aria racchiusa nella cavità orale. Helmholtz rilevò che i toni propri della cavità orale prescindono sostanzialmente dall'età e dal sesso. L'analisi divenne ancora più esatta con l'impiego dei suoi risonatori, costituiti da una serie di cavità sferoidali di varie dimensioni. Avvicinando all'orecchio uno di questi risonatori si ha il massimo rafforzamento del tono parziale di una vocale per mezzo della risonanza, coincidente con il tono proprio del risonatore.

In base alla posizione della cavità orale le vocali si dividono in tre serie: A-E-I, A-Ö-Ü e A-O-U, come già indicato in linea di massima da Chladni nel 1824 e, più tardi nel 1862, da Felix Henry Du Bois-Reymond.

Punto di partenza comune è la vocale A, per pronunciare la quale la cavità orale assume una forma che si allarga a imbuto in maniera abbastanza omogenea. Nelle vocali della serie inferiore la cavità orale viene ridotta con le labbra e somiglia a una bottiglia senza collo. Helmholtz riscontrò in questo caso un unico tono proprio con forte risonanza. Nelle vocali della serie superiore la cavità della bocca assume la forma di una bottiglia con collo stretto, mentre nelle vocali della serie centrale la sua forma è quella di una bottiglia dal collo lungo: il ricercatore trovò due toni propri corrispondenti, uno per il corpo della bottiglia e l'altro per il collo. Helmholtz individuò i valori di questi toni come note musicali, leggermente diversi nei vari dialetti e nelle varie lingue.

Il concetto di 'formante', importante per gli sviluppi successivi dell'acustica, fu introdotto soltanto alcuni decenni dopo dal fisiologo Ludimar Hermann (1838-1914).

Nel 1858 Helmholtz costruì un apparato in grado di determinare il timbro, ossia una sorta di sintetizzatore che rendeva possibile la riproduzione delle varie vocali del linguaggio umano. Un diapason, che era collocato davanti a un tubo di risonanza la cui apertura poteva essere variata, veniva indotto a vibrare mediante stimolazione elettromagnetica. Quando il risonatore era accordato con il diapason, il tono si sentiva forte; inoltre, in questo caso, esso doveva essere posto direttamente davanti al diapason. Coprendo parzialmente il tubo era possibile conferire al tono la forza desiderata. Il sintetizzatore era interamente costituito da una serie di apparati di tale genere dotati di diapason diversi; in questa maniera si potevano rendere udibili, anche a differenti livelli di intensità, varie associazioni diverse della tonica con uno o più toni armonici superiori.

Questo apparecchio offriva possibilità ideali di sperimentazione, perché il suono veniva prodotto con frequenza e volume costanti e per una durata arbitraria. Helmholtz lo usò per riprodurre e ricostruire le vocali ed esso gli consentì di rispondere sia al quesito se i rapporti si modifichino o meno quando la tonica ha un'altra frequenza, sia alla questione dell'influsso che i rapporti di fase della tonica esercitano sul timbro rispetto ai toni armonici superiori. Invertendo la corrente negli elettromagneti era infatti possibile modificare la fase; il medesimo risultato si produceva anche mediante la scordatura dei tubi di risonanza, ottenuta restringendone un po' l'imboccatura. L'esito della prova mostrava che le fasi sono indipendenti rispetto al timbro.

Benché nel 1881 contro questo risultato si esprimesse fra gli altri Karl Rudolph König (1832-1901), l'acustica seguì per un centinaio di anni i risultati di Helmholtz e soltanto di recente si è riconosciuto che le variazioni di fase fra i componenti del tono hanno un'importanza, sia pure secondaria, nell'impressione del timbro.

Per completezza occorre accennare brevemente anche ai lavori di Helmholtz sull'acustica degli strumenti musicali. Era già noto da tempo che per calcolare la frequenza di una canna d'organo aperta non fosse sufficiente conoscere la sua lunghezza l e che fosse invece necessario aggiungere a essa una certa quantità s: con l+s si indica la lunghezza effettiva della canna. La causa del fenomeno risiede nel fatto che le onde piane in una canna devono trasformarsi in sferiche alla terminazione aperta e che questa trasformazione si verifica costantemente. La teoria di Helmholtz in proposito è molto generale e fornisce una formula per s. Nel 1861 egli pubblicò una teoria delle canne ad ancia, per tubi cilindrici e conici, secondo la quale il movimento della linguetta elastica viene determinato per effetto della pressione dell'aria che periodicamente varia nel tubo. Infine, nel 1860 Helmholtz ampliò le conoscenze sul funzionamento del violino con uno studio dedicato al movimento delle corde musicali allorché viene prodotto il suono. Utilizzando il microscopio a vibrazioni da lui sviluppato ‒ una specie di oscilloscopio ‒ potevano essere osservate le figure di Lissajous prodotte dal moto di corde musicali. A prescindere dal punto in cui la corda del violino viene toccata dall'archetto, i movimenti della corda musicale come funzione del tempo hanno sempre la forma di una curva seghettata.

Helmholtz cominciò a redigere a Heidelberg, probabilmente nel 1860, un manoscritto che quando venne completato nell'ottobre del 1862, fu intitolato Die Lehre von der Tonempfindungen als physiologische Grundlage für die Theorie der Musik (La scienza della percezione dei toni come fondamento fisiologico della teoria della musica) e pubblicato a Braunschweig agli inizi del 1863 per i tipi dell'editore Friedrich Vieweg & Sohn. Nell'introduzione, l'autore si esprime in merito al senso e allo scopo dell'opera nel modo seguente:

Il presente libro cerca di unificare quelle aree di confine tra le scienze che, sebbene riferibili l'una all'altra in virtù di molti rapporti naturali, sono ciononostante rimaste finora abbastanza divise e soltanto affiancate, vale a dire le aree di confine dell'acustica fisica e fisiologica da una parte e, della scienza musicale e dell'estetica dall'altra. Esso si rivolge dunque a lettori che abbiano compiuto un percorso di formazione molto vario e che abbiano interessi tra loro assai diversi. (Helmholtz 1863 [1913, p. 1])

Il libro fu riedito più volte in rapida successione; la quarta edizione (1877) fu l'ultima redatta personalmente da Helmholtz, mentre la quinta (1896) e la sesta (1913) furono curate dal fisico Richard Wachsmut; risale al 1868 la traduzione in francese, mentre nel 1895 si pubblicava già la terza edizione inglese. Nel primo capitolo, intitolato Die Zusammensetzung der Schwingungen (La composizione delle vibrazioni), sono trattati i toni armonici superiori e i timbri; nel secondo, Die Störungen des Zusammenklangs (Disturbi della consonanza), egli discute i toni di combinazione e i battimenti e descrive consonanza e dissonanza. Mentre il materiale del primo capitolo costituisce una commistione di punti di vista fisici e fisiologici, il secondo associa questioni fisiche e psicologiche. Il terzo capitolo, quello finale, Die Verwandtschaft der Klänge (Affinità dei timbri), descrive scale tonali e questioni relative alla tonalità, con una prevalenza di problematiche psicologiche ed estetiche concernenti la musica.

Le parole che Helmholtz scrisse alla fine della sua introduzione alla prima edizione sono sostanzialmente un riassunto della storia dell'acustica:

Della scienza del suono è stata trattata finora in maniera esauriente soltanto la parte fisica, indagando i movimenti eseguiti da corpi sonori solidi, liquidi o aeriformi che producono suoni percettibili all'orecchio. Questa acustica fisica nella sua natura altro non è che una parte della scienza dei movimenti dei corpi elastici […]. Accanto all'acustica fisica ne esiste una fisiologica, che deve indagare i processi che si verificano nell'orecchio stesso. Di questa scienza la parte che tratta la propagazione del movimento del suono dall'ingresso nell'orecchio fino alle terminazioni nervose nel labirinto interno è stata in vario modo elaborata […]. In verità va anche detto, nello stesso tempo, che in questo campo non si sono ancora raggiunti molti risultati certi […]. La ricerca sui processi di funzionamento di ciascuno dei nostri organi di senso comprende in generale tre diversi campi d'indagine. In primo luogo occorre indagare come l'impulso che stimola la sensazione, ovvero la luce nel caso dell'occhio e il suono per l'orecchio, vengano condotti fino ai nervi sensibili. Possiamo definire questa prima parte come la sezione fisica della corrispondente ricerca fisiologica. Secondariamente vanno indagati i vari stimoli stessi che agiscono sulle terminazioni nervose, corrispondenti alle diverse sensazioni, e infine le leggi in base alle quali tali sensazioni inducono la formazione di idee relative a determinati oggetti esterni, dando vita alle percezioni. Si ha dunque una parte della ricerca, a dominante fisiologica, che tratta le sensazioni, e una psicologica che tratta le percezioni. Mentre per la scienza dell'udito la parte fisica è già stata considerata sotto molti aspetti, per le parti fisiologica e psicologica disponiamo finora nella scienza soltanto di dettagli incompleti e casuali […]. (Helmholtz 1863 [1913, pp. 5-6])

Questa lunga citazione non costituisce solamente una panoramica storica ma indica anche i temi più importanti della ricerca successiva toccati per primo da Helmholtz.

Lord Rayleigh e l'acustica

di Myles W. Jackson

John W. Strutt (lord Rayleigh, 1842-1919) fu uno dei principali fisici sperimentali britannici tra la fine del XIX e l'inizio del XX secolo. Le sue prime ricerche a Cambridge riguardarono le correnti alternate in un galvanometro; alla fine degli anni Sessanta, però, dopo aver letto il voluminoso tomo di Hermann von Helmholtz Die Lehre von der Tonempfindungen als physiologische Grundlage für die Theorie der Musik, dirottò i propri interessi sull'acustica. I suoi contributi a tale disciplina, assai numerosi e importanti, constano di 128 articoli pubblicati tra il 1870 e il 1919, nonché del volume The theory of sound.

La risonanza acustica

Il primo scritto di Rayleigh sull'acustica, un lungo testo pubblicato nel 1870 sulle "Philosophical Transactions" della Royal Society, fu ispirato dagli studi sui risonatori acustici di Helmholtz, autore, a partire dalla fine degli anni Sessanta, insieme a Wilhelm Weber e Georg Simon Ohm di molti lavori sperimentali e teorici sull'acustica. Nel suo studio Rayleigh fornì una teoria matematica basata su misure accurate e introdusse per la prima volta il concetto critico di conducibilità acustica di un orifizio. I risonatori sono recipienti chiusi a un'estremità e aperti dall'altra; il diametro del condotto è piuttosto piccolo, quindi le vibrazioni prodotte dal condotto tendono a persistere; più è stretto il canale tra l'interno del recipiente e il mezzo esterno, più le vibrazioni interne sono indipendenti dal mezzo. In presenza di una sorgente esterna di suono, l'aria contenuta nel recipiente vibra all'unisono e l'ampiezza della vibrazione dipende dalle grandezze relative dei periodi naturale e forzato. Quando la sorgente esterna smette di suonare, il risonatore continua a vibrare, diventando perciò una sorgente sonora secondaria per un determinato intervallo di tempo.

Nel suo articolo Rayleigh si occupò inoltre della teoria delle vibrazioni dell'aria e del calcolo della nota musicale fondamentale prodotta da un fiasco o da una bottiglia, date le proprietà note dell'aria. Come sempre, egli verificò il proprio calcolo teorico mediante una rigorosa sperimentazione. Rayleigh determinò la risonanza di un corpo particolare, mantenendolo sopra una corda di un pianoforte, utilizzato come banco di laboratorio per esperimenti elettrici, oltre che per dimostrazioni e determinazioni di acustica. Egli indicò che le variazioni di pressione si propagano istantaneamente all'interno di un recipiente, cosicché la pressione è la stessa in ogni istante, e che il fenomeno è guidato dal movimento alternato dell'aria nel collo di una bottiglia o di un fiasco: nel collo, la variabile fondamentale è la velocità dell'aria, mentre all'interno del recipiente ciò che conta è la pressione. Un risonatore a bottiglia è pertanto diverso e più semplice di una canna d'organo, dove, come Helmholtz aveva illustrato nel 1861, devono essere considerate, per ogni punto, sia l'inerzia sia le differenze di pressione nel recipiente, cioè deve essere determinato il tempo che occorre al suono per viaggiare attraverso il recipiente risonante.

Rayleigh divise il suo articolo in due parti; la prima riguardante la teoria generale della risonanza dell'aria in spazi confinati da pareti rigide e comunicanti con passaggi esterni per l'aria (con lunghezza dei colli e dimensioni del recipiente piccole rispetto alla lunghezza d'onda), teoria che si applica soltanto alla nota fondamentale, non alle armoniche superiori; la seconda parte tratta invece il calcolo della conducibilità acustica del passaggio.

La teoria del suono

Nel 1872 Rayleigh decise di scrivere un trattato di acustica. Il suo obiettivo era di elaborare una teoria del suono che includesse i progressi più recenti dei matematici e dei fisici. I lavori di questi scienziati, lamentava Rayleigh, erano stati scritti in lingue diverse, in special modo tedesco e francese, e pubblicati in periodici scarsamente diffusi e in atti di varie società. Inoltre, dall'articolo sul suono di John Herschel nell'Encyclopaedia Metropolitana del 1845, nessuno studio matematico era stato effettuato sulla teoria acustica.

Un anno dopo Rayleigh, durante un viaggio sul Nilo, iniziò a scrivere il suo famoso lavoro, The theory of sound. Un libro in inglese sull'acustica era, secondo i fisici del periodo, atteso da lungo tempo. James C. Maxwell, professore di fisica sperimentale dell'Università di Cambridge, il 20 maggio 1873 scrisse al suo giovane collega:

Mio caro Strutt, sono lieto che stiate scrivendo un libro sull'acustica […]. Voi parlate modestamente di una esigenza di buoni libri in inglese. Ma in nessuna lingua ve ne sono, eccetto l'Helmholtz, che è valido non perché è tedesco ma perché è Helmholtz. Il secondo miglior libro è l'Herschel [John], che può essere considerato di provenienza strutturale tedesca. Prendete in considerazione la teoria di Deschanel secondo la quale il suono di una canna d'organo è eccitato dalla vibrazione dello spesso bordo di legno dell'imboccatura: "Questo bordo è di per sé stesso capace di vibrare all'unisono con ogni nota giacente entro un largo intervallo e la nota che è effettivamente emessa è determinata dalla risonanza della colonna d'aria nella canna".

Questo è quanto gli organisti desiderosi di conoscenza scientifica devono accettare per vero e credere. Un'altra convinzione trasmessa a queste persone è che chiunque, con una semplice infarinatura scientifica, dovrebbe comprendere completamente il moto dell'imboccatura, diciamo, del flauto. (in Strutt 1968, pp. 80-81)

Nel 1876 Rayleigh vergò il suo manoscritto sul retro dei saggi degli studenti del Mathematical Tripos dell'Università di Cambridge e nel 1877 l'editore Macmillan di Londra lo pubblicò in due volumi.

A proposito dei volumi ricevuti, Edward J. Routh (1831-1907) scrisse a Rayleigh: "Il libro sul suono più richiesto è arrivato appena prima che io lasciassi Cambridge […] non c'è bisogno di dire che sembra proprio quello che vogliamo. In questa prossima lunga (vacanza) lo userò, naturalmente, come libro di testo e spero di imparare molto da esso. Suppongo che faremo ora sull'argomento molti più progressi di quanti non ne abbiamo mai fatti" (ibidem, pp. 83-84).

George B. Airy (1801-1892), professore di astronomia dell'Università di Cambridge, scrisse: "Signore, sono molto obbligato per il regalo di una copia del lavoro sul 'Suono' della Signoria Vostra, che ho ricevuto dai Signori Macmillan. Il lavoro evidentemente contiene le più profonde disamine non soltanto sul suono propriamente detto ma anche sulle vibrazioni non sonore e il tutto è stato sviluppato con una matematica approfondita applicabile a soggetti persino più complicati. Meriterebbe quasi un titolo di più ampio significato" (ibidem, p. 84).

Helmholtz elogiò il lavoro su "Nature": sottolineando quanto fosse coerente e accessibile, lo paragonò perfino al magistrale Treatise on natural philosophy (1867) di William Thomson (lord Kelvin, 1824-1907) e Peter Guthrie Tait (1831-1901), auspicando che Rayleigh scrivesse un terzo volume sulla teoria dei tubi sonori ad ancia e, in particolar modo, sulla voce umana; Helmholtz così si espresse: "Almeno per la prima è già possibile fornire i principî meccanici, e i metodi che l'autore impiega a me sembrano particolarmente adatti a favorire un ulteriore progresso in questi ambiti" (in Strutt 1968, p. 84). Egli voleva anche che Rayleigh trattasse, in questo terzo volume, le fiamme cantanti, l'azione di un archetto di violino su una corda e altre forme di mantenimento delle oscillazioni. Rayleigh prese in seria considerazione l'idea di scrivere un terzo volume, che poi non realizzò; discusse comunque alcuni di questi argomenti nella seconda edizione del suo lavoro, mentre la prima fu tradotta in tedesco da F. Neesen nel 1878 su sollecitazione di Helmholtz.

Rayleigh si limitò a occuparsi delle classi di vibrazioni alle quali è sensibile l'orecchio umano. Il primo volume è dedicato allo studio in generale delle vibrazioni di sistemi come corde tese, sbarre, membrane e piatti, mentre il secondo volume riguarda le vibrazioni dell'aria. In preparazione di tale lavoro, egli espose dettagliatamente la teoria generale delle vibrazioni di un sistema dinamico intorno al suo stato di equilibrio, soffermandosi su tre punti piuttosto interessanti: prima di tutto osservò che l'aumento di massa di una qualunque parte del sistema vibrante non si traduce mai in una diminuzione del periodo del suo moto; introdusse poi la sua nota funzione di dissipazione: le forze di smorzamento che riguardano un sistema dinamico sono dovute sia all'attrito sia alla viscosità e ciascuna particella del sistema è smorzata o ritardata da forze proporzionali alle sue velocità componenti. La funzione di dissipazione di Rayleigh implica una relazione tra i coefficienti delle equazioni generalizzate delle vibrazioni. Dimostrò infine il teorema generale di reciprocità, includendo come caso speciale quello di Helmholtz; quest'ultimo teorema mette a confronto l'efficienza dei dispositivi acustici quali emettitori e ricevitori di energia radiativa. Helmholtz estese il teorema di Green argomentando che, dato uno spazio riempito d'aria parzialmente delimitato da corpi fissi di estensione finita, si possono eccitare onde sonore in un punto A in modo tale che il potenziale di velocità risultante in un secondo punto B sia lo stesso, in grandezza e in fase, di quello che sarebbe stato in A se B fosse stata la sorgente del suono. Secondo Rayleigh, la reciprocità vale perfino in presenza di forze dissipative e anche se il fluido non è omogeneo, né i corpi vicini, fissi e rigidi. Egli argomenta che la forma di Helmholtz del teorema di reciprocità è applicabile soltanto a sorgenti semplici di suono, quelle che generano onde simmetriche.

Il lavoro di Rayleigh sulla reciprocità, uno dei suoi più importanti contributi all'acustica, era applicabile a una sorgente di suono semplice nell'aria: all'aperto la sorgente avrebbe suonato in modo uguale in tutte le direzioni. Esperimenti condotti da John Tyndall (1820-1893), caro amico e collega di Rayleigh, alla Royal Institution di Londra sembrarono confutare il suo teorema. L'apparato sperimentale di Tyndall era composto, piuttosto semplicemente, da una canna che produceva un suono acuto e da una fiamma, altamente sensibile, che brillava quando era esposta a un tono alto. Egli notò che uno schermo di vetro posto tra la canna e il getto luminoso riduceva la fiammata in misura maggiore quando era avvicinato alla canna; tale fenomeno contraddiceva, chiaramente, il principio di reciprocità. Rayleigh, turbato dai risultati del suo amico, si recò presso la Royal Institution per partecipare personalmente all'esperimento: l'assistente di laboratorio di Tyndall, Cottrell, lo convinse riproducendo l'effetto; tuttavia, un'altra prova eseguita dallo stesso assistente fornì a Rayleigh un indizio per una spiegazione capace di giustificare il teorema di reciprocità.

La teoria della reciprocità si fonda sul presupposto che il suono sia emesso da una sorgente in tutte le direzioni con uguale intensità. Precedentemente si era assunto che i tubi ad ancia fossero in grado di soddisfare questa condizione, tuttavia Cottrell dimostrò che quei tubi emettono un suono che è altamente direzionale. Di conseguenza, se il tubo è puntato verso la fiamma, essa brilla con un'intensità maggiore di quando il tubo stesso è puntato altrove. Quindi, la reciprocità era ancora valida.

La seconda edizione di The theory of sound apparve tra il 1894 e il 1896. Rayleigh ampliò i due volumi originali aggiungendo la trattazione di alcuni argomenti, tra cui le campane, i tubi ad ancia, le fiamme cantanti, l'insufflazione delle canne d'organo (distinta dalla risonanza), la repulsione dei risonatori, l'attrito e la conduzione del calore in acustica, la capillarità e le onde di capillarità, il moto vorticoso e le teorie sull'udito; egli incluse perfino un capitolo sul telefono, che trattava le correnti alternate e la loro distribuzione in una rete di conduttori.

Il lavoro di Rayleigh è suddiviso in due sezioni principali: la produzione e la propagazione del suono. Nella prima sono esaminate le vibrazioni dei sistemi dinamici, con speciale attenzione verso l'irradiazione del suono. Il capitolo 1 concerne i casi più semplici, ovvero le oscillazioni di un sistema con un solo grado di libertà, mentre i due capitoli seguenti discutono la teoria generale delle vibrazioni a n gradi di libertà; in questa trattazione Rayleigh mostra il procedimento di approssimazione della più bassa frequenza di vibrazione di un sistema, per il quale è impossibile fornire una soluzione esatta usando le equazioni differenziali, basandosi sulle energie potenziale e cinetica massime, secondo un metodo più tardi chiamato il metodo di Rayleigh-Ritz. I capitoli 4 e 5 trattano i sistemi vibranti, con il calcolo delle espressioni per le energie potenziali e cinetiche e la derivazione del teorema di reciprocità. Nel capitolo 6 Rayleigh analizza le vibrazioni trasversali delle corde e analizza la fisica del pizzicamento di queste ultime, il ruolo dell'attrito sulle corde del pianoforte e del violino e le vibrazioni stazionarie. I capitoli 7 e 8 offrono un resoconto dettagliato delle vibrazioni longitudinali, di torsione e laterali delle sbarre. Nel capitolo 9 sono trattate principalmente le vibrazioni delle membrane e, in particolare, la relazione tra la tonalità e l'area di una membrana (specialmente quella dei timpani). Il capitolo 10 discute le vibrazioni dei piatti, con particolare attenzione per le energie potenziale e cinetica coinvolte nelle vibrazioni, comprese quelle elettriche.

Nel secondo volume Rayleigh affronta come primo argomento, nel capitolo 11, le vibrazioni dell'aria servendosi di un'elaborazione delle sue ricerche sui risonatori del 1870. Il capitolo 12 analizza le vibrazioni nei tubi, mentre il capitolo 13 discute la riflessione e la rifrazione delle onde piane in relazione al problema generale delle vibrazioni dell'aria. I due capitoli successivi esaminano le equazioni generali delle vibrazioni dell'aria in tre dimensioni. Il capitolo 16 presenta minuziosamente la teoria di Rayleigh dei risonatori esposta precedentemente. Nel capitolo 17, le funzioni di Laplace sono applicate a problemi acustici, mentre nel capitolo 18 si considera uno strato sferico di aria per verificare l'espressione di Laplace per una funzione che è arbitraria in ogni punto di una superficie sferica. Il capitolo 19 analizza le vibrazioni dell'aria in tubi stretti, dove la viscosità e il calore di compressione giocano un ruolo cruciale. La spiegazione delle vibrazioni capillari costituisce la base del capitolo 20, mentre la sensibilità di fiamme e di getti di fumo alle vibrazioni è il soggetto del capitolo seguente. Il capitolo 22 offre un abbozzo della teoria delle vibrazioni dei solidi elastici, con riferimento alla propagazione delle onde piane. Il capitolo conclusivo espone una pletora di fatti, osservazioni e teorie sull'udito, che si rifanno ancora una volta al precedente lavoro di Helmholtz.

Dopo la pubblicazione della prima edizione di The theory of sound, Rayleigh lavorò su uno strumento per misurare l'intensità del suono: si trattava di un piccolo disco sospeso a un filo di torsione che, investito da un'onda acustica, ruotava disponendosi in una posizione di equilibrio; l'intensità dell'onda era ricavata dall'ampiezza dell'angolo di rotazione del disco. Lo strumento è usato ancora oggi con il nome di 'disco di Rayleigh'.

Un anno dopo, Rayleigh descrisse il fenomeno della corrente acustica, basato sull'influenza dell'attrito sul moto dei fluidi in prossimità dei corpi solidi. Egli discusse tre problemi: il primo riguardava le correnti generate su un piatto vibrante (come scoperto da Chladni), il secondo il fenomeno del colore osservato su pellicole di liquido affette da vibrazioni sonore e l'ultimo le correnti d'aria osservate in un tubo di Kundt. Nel 1899 Rayleigh propose il meccanismo di rilassamento al fine di spiegare l'attenuazione del suono nei mezzi materiali, ipotesi che andò a formare la spina dorsale della ricerca del XX sec. nell'ambito dell'acustica molecolare, in special modo nella propagazione del suono.

Bibliografia

Glazebrook 1910: Glazebrook, Richard T., The Rayleigh period, in: A history of the Cavendish laboratory, 1871-1910, London, Longmans, 1910.

Lindsay 1970: Lindsay, Robert B., Men of physics. Lord Rayleigh. The man and his work, Oxford-New York, Pergamon, 1970.

Rechenberg 1994: Rechenberg, Helmut, Hermann von Helmholtz. Bilder seines Lebens und Wirkens, Weinheim-New York, Verlag Chimie, 1994.

Roederer 1993: Roederer, Juan G., Physikalische und psychoakustische Grundlagen der Musik, 2. ed., Berlin, Springer, 1993 (1. ed.: 1977; ed. orig.: Introduction to the physics and psychophysics of music, London, The English Universities Press, 1973).

Strutt 1968: Strutt, Robert John, fourth Baron Rayleigh, The life of John William Strutt, third baron Rayleigh, Madison, University of Wisconsin Press, 1968.

Turner 1977: Turner, R. Steven, The Ohm-Seebeck dispute, Hermann von Helmholtz and the origins of physiological acoustics, "The British journal for the history of science", 10, 1977, pp. 1-24.