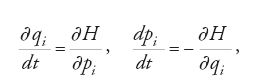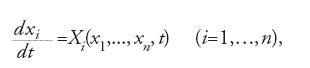L'Ottocento: astronomia. Il problema dei tre corpi e la stabilità del Sistema solare
L'Ottocento: astronomia. Il problema dei tre corpi e la stabilita del Sistema solare
Il problema dei tre corpi e la stabilità del Sistema solare
Questo capitolo illustra, a grandi linee, la storia del problema dei tre corpi, fornisce una breve panoramica degli scritti su questo tema e mostra quale legame vi sia fra il problema dei tre corpi e quello della stabilità del Sistema solare. In particolare, le pagine che seguono sono incentrate sul contributo fondamentale di Jules-Henri Poincaré (1854-1912), il cui tentativo di risolvere il problema in questione lo portò alla scoperta del caos matematico.
La formulazione del problema dei tre corpi è semplice: tre punti materiali si muovono nello spazio, sottoposti a mutua attrazione gravitazionale; fissate le loro condizioni iniziali, si tratta di determinarne il moto negli istanti successivi. Il problema può quindi essere descritto da un sistema di nove equazioni differenziali ordinarie del secondo ordine. È immediata l'estensione al caso di un numero n qualsiasi di masse, che prende il nome di problema degli n corpi.
Nel corso del tempo i tentativi di trovare una soluzione al problema dei tre corpi hanno stimolato numerose ricerche. Tra la metà del XVIII e l'inizio del XX sec. gli furono dedicati più di 800 articoli, anche di matematici e astronomi famosi. Oggi se ne riconosce l'importanza, sia come problema in sé, sia per i progressi matematici che la ricerca di una sua soluzione ha generato in molti campi diversi, ai quali si è aggiunta recentemente la teoria dei sistemi dinamici.
Un ruolo importante nella ricerca, sia per la semplicità della sua formulazione sia per le applicazioni pratiche, lo ha avuto un caso particolare del problema dei tre corpi, ovvero quello che Poincaré chiamò problema 'ristretto'. In esso vengono considerati due corpi, detti 'primari', che, sottoposti alla reciproca attrazione gravitazionale, ruotano su orbite circolari attorno al proprio centro di massa e formano così un sistema di due corpi dei quali è noto il moto; un terzo corpo, detto 'pianetino', talmente leggero da non influenzare il moto dei due corpi primari, si muove sul piano individuato dalla loro orbita e subisce gli effetti della loro attrazione gravitazionale; il problema consiste nel descrivere il moto di questo pianetino.
Il problema 'ristretto' dei tre corpi è, tra le possibili riduzioni non banali del problema originale, quella più semplice; esso inoltre è particolarmente importante nell'ambito delle ricerche di Poincaré, in quanto gran parte dei risultati da lui raggiunti scaturisce da questa formulazione. Essa, oltre a semplificare il problema dei tre corpi, costituisce una buona approssimazione di situazioni fisiche reali, in particolare quella riguardante il moto della Luna intorno alla Terra quando si consideri anche l'influenza del Sole, oppure lo studio di un sistema formato dal Sole, da Giove e da un piccolo pianeta o da un asteroide.
Il problema dei tre corpi possiede un'altra caratteristica, che spiega molti dei tentativi messi in atto per risolverlo: lo stretto legame con la questione fondamentale relativa alla stabilità del Sistema solare. Non sappiamo, infatti, se esso conserverà per sempre la sua struttura attuale oppure, a un certo punto, uno dei suoi pianeti se ne allontanerà o, peggio ancora, subirà una collisione. È questa una questione che interessa gli astronomi da secoli, sin dal momento in cui ci si accorse che il moto della Terra e degli altri pianeti non è esattamente periodico e regolare.
I corpi del Sistema solare, essendo approssimativamente sferici e di dimensioni estremamente piccole in rapporto alle distanze reciproche, possono essere considerati punti materiali. In base alla legge di Newton, le orbite lungo le quali essi si muovono sono, in prima approssimazione, ellissi, con il Sole in uno dei due fuochi. Si tratta di una prima approssimazione perché in essa si tiene conto soltanto dell'interazione tra il Sole e il singolo pianeta di cui si descrive l'orbita, ma non si considerano le forze agenti tra i vari pianeti. Queste forze perturbano l'orbita ellittica facendola variare molto lentamente; non si può quindi escludere che, in un lontano futuro, tale perturbazione sia in grado di modificare le orbite attuali fino a causare l'espulsione di un pianeta dal Sistema solare o a provocarne una collisione. Anche se le osservazioni astronomiche degli ultimi mille anni non concordano con questo scenario, ben altro è dimostrare matematicamente che esso non potrà mai presentarsi e proprio la ricerca di una tale dimostrazione matematica è alla base dell'interesse per il problema dei tre corpi. Se quindi si considera solamente la forza di gravità e si trascurano tutte le altre quali, per esempio, i venti solari o gli effetti relativistici, è possibile trattare il Sistema solare come un problema dei dieci corpi, di cui uno grande (il Sole) e gli altri nove piccoli.
I precedenti
L'origine del problema può essere fatta coincidere con quella dell'astronomia dinamica moderna, che risale all'introduzione della teoria della gravitazione da parte di Newton. Sin dalla pubblicazione dei Principia nel 1687, divenne importante verificare se la legge di Newton e la sua teoria della gravitazione potessero rendere conto in modo completo del moto dei corpi celesti nello spazio tridimensionale.
Newton risolse geometricamente il problema dei due corpi, considerando due sfere in movimento sottoposte all'attrazione gravitazionale reciproca, e nel 1710 Johann I Bernoulli dimostrò che la traiettoria di una particella rispetto all'altra è descritta da una sezione conica. Nel 1734 Daniel Bernoulli vinse un premio dell'Académie des Sciences di Parigi per la sua trattazione analitica del problema dei due corpi, poi risolto in dettaglio da Leonhard Euler nel 1744. Ricerche sul problema più complesso riguardante più di due corpi erano già allora in corso. In base all'esigenza dei naviganti di conoscere con grande precisione il moto della Luna, il sistema formato da Sole, Terra e Luna era da tempo oggetto di studio e la teoria lunare ebbe un ruolo dominante nelle prime ricerche sul problema dei tre corpi. Gli studi presero due direzioni: trovare teoremi generali che descrivessero le proprietà del moto e cercare soluzioni approssimate, valide per un certo intervallo temporale, a partire da un istante per il quale i dati erano noti.
Newton, il primo a trattare il problema dei tre corpi, ottenne risultati in entrambe le direzioni. Dopo aver mostrato che il centro di massa di n corpi si muove con velocità uniforme lungo una retta, studiò in generale il moto di corpi che si attraggono reciprocamente e, pur usando in modo essenzialmente geometrico il metodo della variazione dei parametri, applicò la teoria delle perturbazioni allo studio del moto lunare. I calcoli gli crearono tuttavia notevoli difficoltà e la sua determinazione del moto degli apsidi lunari fornì un valore che era circa la metà di quello osservato. In effetti i problemi che incontrò furono tali da indurlo in seguito a ricordare che non aveva mai sofferto tanto di mal di testa come durante i suoi studi sulla Luna.
Nel 1760 Euler iniziò a prendere in esame versioni semplificate del problema dei tre corpi. Partendo dal caso in cui due delle masse sono fisse nello spazio e la terza si muove nel loro campo gravitazionale, ottenne soluzioni dipendenti da integrali ellittici. Nel 1762 enunciò per la prima volta il problema ristretto e dimostrò l'esistenza di soluzioni collineari, in cui le tre masse restano sempre allineate (Euler 1767). In seguito, nel 1772, in una memoria sulla teoria del moto della Luna che, assieme a un'altra di Joseph-Louis Lagrange, fu premiata dall'Académie, Euler presentò la prima formulazione del problema ristretto basato su un sistema di coordinate rotanti. Come egli stesso osservò, in un opportuno sistema di riferimento rotante i corpi primari appaiono stazionari e, poiché la posizione e la velocità del pianetino sono individuate ciascuna da due coordinate, si ha un sistema con due gradi di libertà. Euler ridusse inoltre il problema generale da un sistema di equazioni di ordine diciotto a uno di ordine otto, mediante l'uso dei sei integrali del moto del centro di massa, dei tre integrali del momento angolare (o momento della quantità di moto) e dell'integrale dell'energia.
La memoria di Lagrange, premiata e molto apprezzata dall'Académie, analizzava il problema dei tre corpi mostrando di poterlo ridurre, con l'uso degli integrali del momento della quantità di moto e dell'energia, a un sistema di ordine sette. Il suo metodo consisteva nel determinare dapprima le distanze reciproche tra i corpi, per poi individuare, nello spazio, il piano contenente il triangolo con ai vertici le tre masse e infine nel determinare l'orientazione del triangolo nel piano. Le equazioni così ottenute ammettevano due tipi particolari di soluzioni: una, già trovata da Euler, in cui le tre masse si muovono sempre allineate, l'altra in cui i corpi si trovano sempre ai vertici di un triangolo equilatero in movimento.
Esistono cinque punti di equilibrio associati a tali soluzioni particolari, detti anche punti 'lagrangiani' o 'di librazione'. Fisicamente essi corrispondono ai punti nei quali, nel sistema rotante, le forze agenti sul terzo corpo si bilanciano, in modo tale che rispetto a questo sistema di riferimento non si manifesti alcun moto. Nonostante Lagrange ritenesse che tali soluzioni non potessero realizzarsi in pratica, la dimostrazione dell'esistenza di punti di equilibrio triangolari nel sistema Sole-Giove previde di fatto l'esistenza degli asteroidi cosiddetti 'Troiani', che furono effettivamente osservati solamente nel 1906 allorché Max Wolf scoprì l'asteroide Achille.
Nel 1836 Carl Gustav Jacob Jacobi (1804-1851) scoprì un nuovo integrale del moto per il problema ristretto, oggi detto 'integrale di Jacobi', riducendo così tale problema a uno di ordine tre. Nel 1843, pur non conoscendo il precedente lavoro di Lagrange, egli ridusse a sei l'ordine del problema generale. Questa ulteriore riduzione fu ottenuta con la cosiddetta 'eliminazione dei nodi', un procedimento che, secondo Edmund T. Whittaker (1937), era già stato indicato da Lagrange. Jacobi, avvalendosi inizialmente di una trasformazione lineare, ottenne nuove variabili rispetto alle quali due corpi 'fittizi' risultano orbitanti attorno a un terzo. Grazie alla linearità del cambiamento di variabili, la forma degli integrali del momento della quantità di moto resta immutata, mentre il vettore del momento della quantità di moto totale rimane costante e perpendicolare a un piano invariante. Jacobi mostrò inoltre che l'intersezione dei piani orbitali dei due corpi si mantiene parallela al piano invariante, da cui segue che la differenza in longitudine tra i nodi ascendenti è sempre di π radianti.
Jacobi contribuì anche a sviluppare nuovi metodi per integrare le equazioni differenziali di un sistema dinamico generale, metodi particolarmente utili per il problema in questione. La teoria che oggi viene chiamata di Hamilton-Jacobi traeva origine dalla dinamica lagrangiana e fu enunciata negli anni Trenta del XIXsec. da Sir William R. Hamilton (1805-1865) nel quadro delle sue ricerche sull'ottica matematica e sul problema dei tre corpi. Hamilton espresse le equazioni del moto di un qualsiasi sistema con n gradi di libertà mediante n coppie di equazioni alle derivate parziali del primo ordine:
dove qi rappresenta le coordinate generalizzate, pi sono i momenti generalizzati e H=H(qi,pi) è la funzione hamiltoniana (detta di solito semplicemente 'l'hamiltoniana'), che coincide spesso con l'energia totale del sistema. Hamilton mostrò inoltre che una soluzione delle suddette equazioni poteva essere fornita dalle derivate parziali di una funzione S, che chiamò 'funzione principale'. La teoria fu perfezionata e generalizzata da Jacobi, il quale mostrò che l'hamiltoniana poteva dipendere, oltre che dalle qi e pi, anche dal tempo t. Jacobi avrebbe poi chiamato 'canoniche' le equazioni del moto scritte in forma hamiltoniana. Divenne consuetudine adottare il formalismo canonico per scrivere le equazioni del moto, poiché esso rende più facile la trasformazione delle variabili ‒ una proprietà importante nella semplificazione del problema.
Uno dei contributi più importanti del XVIII sec. al problema della stabilità del Sistema solare fu quello di Pierre-Simon de Laplace (1749-1827), il quale, introducendo i metodi perturbativi, fornì uno strumento fondamentale per la ricerca di una soluzione. Laplace era convinto di poter dedurre la suddetta stabilità dalle leggi di Newton e sperava di dimostrare che le variazioni secolari erano in realtà periodiche, con un periodo estremamente lungo. Il suo primo contributo importante apparve in una memoria ultimata nel 1774, nella quale mostrò che, per perturbazioni del primo ordine rispetto alle masse e approssimando al secondo ordine rispetto alle eccentricità e alle inclinazioni, non vi sono variazioni secolari nei moti medi dei pianeti.
Tra il 1774 e il 1776 Lagrange estese i risultati di Laplace a tutte le potenze delle eccentricità e delle inclinazioni (sempre per perturbazioni del primo ordine rispetto alle masse). Negli anni 1783 e 1784 scrisse due lunghe memorie in cui sviluppò metodicamente sia la teoria delle variazioni secolari, sia quella delle variazioni periodiche, mettendo in evidenza che le proprie precedenti affermazioni sulle variazioni secolari erano state premature. Questi nuovi studi dimostravano infatti che i moti medi avevano effettivamente variazioni secolari, ma solo nella misura in cui dipendevano dalle variazioni secolari degli altri elementi orbitali. Non si trattava però di una difficoltà insormontabile, in quanto i contributi dei termini secolari risultavano così esigui da poter essere tranquillamente trascurati persino nel caso di Giove e Saturno, i due pianeti che mostravano le variazioni maggiori.
Nel 1785 Laplace tornò ancora sul problema, schierandosi decisamente a favore della stabilità. In una serie di cinque memorie scritte tra il 1785 e il 1788 annunciò di aver trovato la soluzione per molte tra le più importanti anomalie della teoria del moto dei pianeti. I suoi contributi più noti includevano la scoperta della disuguaglianza di lungo periodo che si verifica nelle perturbazioni reciproche tra Giove e Saturno e una spiegazione del moto dei satelliti di Giove. Inoltre, dopo diversi tentativi, scoprì anche la causa della variazione secolare del moto medio lunare: essa nasceva dall'azione combinata del Sole con la variazione secolare dell'eccentricità dell'orbita terrestre. Egli era convinto che tali scoperte giustificassero pienamente la sua fiducia nella stabilità del Sistema solare e, nell'ultima memoria della serie, si pronunciò chiaramente in tal senso.
La disuguaglianza di lungo periodo di Giove e Saturno, scoperta da Laplace, è dovuta a termini del terzo ordine nello sviluppo dell'eccentricità e delle inclinazioni e fornisce un esempio particolare del problema dei 'piccoli divisori'. Si tratta di un ben noto problema della meccanica celeste, che sorge nel caso in cui i moti medi siano tra loro, con buona approssimazione, nel rapporto di due numeri interi piccoli. Tale dipendenza razionale conduce a espressioni arbitrariamente prossime allo zero nei denominatori dei coefficienti dello sviluppo in serie della perturbazione. Da un punto di vista dinamico più generale, il problema dei piccoli divisori corrisponde al problema della risonanza prodotta dalla quasi commensurabilità delle frequenze proprie del sistema. Nel caso di Giove e Saturno, il rapporto tra i moti medi è circa 5:2 e lo sviluppo della funzione perturbatrice fornisce termini nei quali è presente l'argomento (5n′−2n)t, dove n′ e n sono i moti medi stessi. Anche se il valore della funzione perturbatrice è piccolo, il suo effetto è sorprendente, in quanto dopo due integrazioni i termini sono moltiplicati per il quadrato del reciproco di (5n′−2n). Il periodo della perturbazione è di circa 900 anni, donde l'espressione 'disuguaglianza di lungo periodo'.
Nel 1809 Siméon-Denis Poisson (1781-1840) rafforzò ulteriormente gli argomenti a favore della stabilità del Sistema solare, migliorando l'approssimazione di Lagrange e mostrando che, fino al secondo ordine rispetto alle masse perturbatrici, non vi sono variazioni secolari nei moti medi dei pianeti. Poisson propose anche una nuova e più generale definizione di stabilità. Anziché richiedere che gli assi maggiori delle ellissi rimanessero compresi entro certi limiti, definì stabile un sistema se esso tornava ripetutamente vicino alla sua configurazione iniziale, indipendentemente da ciò che poteva accadere tra un ritorno e l'altro.
I primi dubbi sulla stabilità furono posti da Spiru Haretu (1851-1912) un giovane rumeno che studiava a Parigi. Nella sua tesi di dottorato del 1878, egli dimostrò che si manifestano variazioni secolari nei moti medi dei pianeti se i calcoli sono eseguiti fino al terzo ordine rispetto alle masse perturbatrici. Il risultato di Haretu non permetteva però di trarre conclusioni interessanti, perché non indicava con esattezza l'entità delle variazioni non implicando necessariamente l'instabilità; ciò portò a un graduale disinteresse sia per tali metodi sia per il lavoro dello stesso Haretu. Questi però aveva indicato che i metodi di approssimazione adottati erano inadeguati a fornire una soluzione definitiva del problema.
Per quanto riguarda il problema dei tre corpi, verso la metà del XIX sec. era ormai chiaro quanto fosse improbabile trovarne una soluzione in forma chiusa. Quindi, come già era accaduto per il problema della stabilità, l'obiettivo divenne quello di migliorare le approssimazioni delle serie di potenze con cui si esprimevano le soluzioni delle equazioni differenziali. Ancora una volta ciò comportò il tentativo di eliminare i termini secolari per poter limitare gli sviluppi in serie nelle quali il tempo comparisse soltanto nell'argomento delle funzioni periodiche.
Tuttavia, proprio dai progressi ottenuti emerse una nuova difficoltà, che traeva origine dal fatto che a occuparsi del problema dei tre corpi e della stabilità erano non tanto i matematici quanto gli astronomi, i quali preferivano le ricerche numeriche a quelle teoriche. Questa diversità di approccio ebbe un'importanza decisiva per il problema, portando a due diversi significati del concetto di convergenza. Gli astronomi consideravano una serie convergente nel caso in cui i termini che riuscivano a calcolare decrescevano rapidamente, anche senza sapere nulla sul comportamento dei termini successivi. I matematici, invece, consideravano convergente una serie soltanto se la convergenza veniva dimostrata rigorosamente. Questa differenza fu sottovalutata; solamente più tardi ci si rese conto che la maggior parte delle serie proposte come soluzioni non era convergente nel senso matematico rigoroso del termine e quindi non era chiaro in quale relazione fossero con la soluzione esatta.
Se, come accade nelle applicazioni pratiche, si fissa in anticipo l'intervallo di tempo che interessa, il calcolo dei primi termini fornisce un'approssimazione del tutto soddisfacente. Tuttavia qualora si intenda usare le serie per stabilire risultati teorici rigorosi e validi per qualsiasi intervallo temporale, come, per esempio, nel caso della dimostrazione della stabilità del Sistema solare, la divergenza delle serie pone seri problemi; inoltre, se le serie sono divergenti, allora non possono, in generale, fornire un'approssimazione arbitrariamente accurata della soluzione. Poincaré, pur dando il dovuto credito alla validità dei risultati degli astronomi‒ e considerando, in particolare, degne di nota le scoperte di Delaunay, Lindstedt e Gyldén ‒, fu il primo a dimostrare che le loro serie erano in generale divergenti.
Charles-Eugène Delaunay (1816-1872) giunse per la prima volta all'eliminazione dei termini secolari nel problema del moto della Luna. Questo risultato fu ottenuto grazie al metodo della variazione dei parametri, tramite il quale egli riuscì a costruire una serie puramente trigonometrica che soddisfaceva, almeno formalmente, le equazioni del moto. La mole dei calcoli effettuati a tal fine fu enorme, tanto che Delaunay impiegò più di vent'anni per completarli. Nel 1846, egli rese pubblica un'esposizione concisa delle idee basilari del suo metodo, ma i risultati finali, contenuti in due grandi volumi, apparvero soltanto nel 1860 e nel 1867.
Nel 1881 l'astronomo finlandese Johan August Hugo Gyldén (1841-1896) iniziò a sviluppare una teoria delle orbite assolute per il calcolo del moto dei pianeti. Il lavoro di Gyldén, basato sull'uso delle funzioni ellittiche, culminò nel 1893 con la pubblicazione del primo volume di quella che, almeno nelle intenzioni, avrebbe dovuto essere una serie di tre volumi dedicati alla teoria; la morte dell'autore impedì però il completamento dell'opera. Il sistema da lui proposto è costituito dal Sole e da due pianeti, ciascuno dei quali può essere considerato o la causa o l'oggetto della perturbazione. Le equazioni differenziali che rappresentano il moto del pianeta perturbato si risolvono ricorrendo a somme di termini periodici, aventi per argomento funzioni lineari rispetto a una quantità che Gyldén chiamò 'longitudine vera' del pianeta. I termini che si annullano quando la massa che perturba è posta uguale a zero si dicono 'termini coordinati' e corrispondono alle variazioni periodiche della teoria classica. I termini che non si annullano con la massa perturbatrice, ma vanno ad aggiungersi a quelli che rappresentano il moto ellittico del pianeta perturbatore attorno al Sole, si dicono 'termini elementari' e corrispondono alle variazioni secolari della teoria classica. Se, nell'esprimere le coordinate, si eliminano tutti i termini coordinati, allora la nuova espressione, contenente soltanto termini elementari, definirà una nuova orbita molto prossima a quella reale (dalla quale si discosterà per un ordine di grandezza pari a quello delle forze perturbatrici). Questa nuova orbita è detta 'orbita assoluta' e le equazioni differenziali si risolvono sostituendo alla funzione perturbatrice un suo sviluppo e poi integrando. Le sei costanti di integrazione arbitrarie sono gli elementi che fissano l'orbita assoluta del corpo perturbato.
Usando come variabile indipendente la longitudine del pianeta, le integrazioni comportavano un gran numero di complesse trasformazioni, e ciò, assieme all'esigenza di mantenere separati i termini elementari da quelli non elementari, complicava estremamente tutto il processo. Inoltre, poiché le costanti di integrazione introdotte da Gyldén rappresentavano quantità fino a quel punto indefinite, la nuova terminologia che egli introdusse per descriverle rese ancora più difficile la comprensione del suo contributo.
Per superare il problema dei denominatori piccoli, Gyldén modificò il coefficiente della prima potenza della variabile dipendente includendo una funzione che chiamò 'oristica' (o limitante). Frutto delle sue ricerche fu la pubblicazione di numerosi e lunghi articoli, nei quali egli riteneva di aver dimostrato la convergenza, ma in realtà, come avrebbe mostrato successivamente Poincaré, le serie che si ottenevano dalle sue deduzioni erano divergenti.
Forse fu proprio per chiarire alcuni aspetti oscuri del lavoro di Gyldén che l'astronomo svedese Anders Lindstedt (1854-1939) si impegnò nella ricerca di soluzioni espresse come serie trigonometriche. Nel 1883 Lindstedt introdusse un metodo capace di integrare una classe importante di equazioni differenziali che si presenta spesso nella teoria delle perturbazioni della meccanica celeste. Tali equazioni, che in sostanza rappresentano un oscillatore armonico perturbato, erano già comparse nelle ricerche di Gyldén e avevano la seguente espressione generale:
dove α è molto piccolo e Φ(x,t) è una funzione sviluppata in serie di potenze di x, aventi per coefficienti funzioni periodiche di t. Il metodo, soggetto ad alcune limitazioni sulla simmetria dei coefficienti, evita l'uso di termini secolari, sia puri sia misti, e mostra come, sviluppando x in serie trigonometrica, si possano soddisfare le equazioni del moto.
Poco dopo, Lindstedt applicò lo stesso metodo per cercare soluzioni espresse in forma di serie trigonometrica al problema dei tre corpi. Egli partì dalle equazioni di Lagrange e poi, assumendo che le eccentricità, il rapporto tra i raggi vettori e le inclinazioni di due dei tre corpi fossero sufficientemente piccoli, ridusse il sistema a quattro equazioni differenziali del secondo ordine. Risolse queste ultime per approssimazioni successive riuscendo a eliminare tutti i termini secolari, in modo da far comparire il tempo solamente negli argomenti delle funzioni periodiche. Ciò lo condusse a rappresentare le coordinate dei tre corpi come serie trigonometriche di quattro argomenti, ciascuno dei quali funzione lineare del tempo. Egli ipotizzò poi (erroneamente) che fosse possibile scegliere le costanti di integrazione in modo da assicurare la convergenza. Anche se Poincaré avrebbe poi scoperto alcuni errori concettuali nel metodo di Lindstedt, esso, da un punto di vista pratico, si rivelò molto utile.
Lindstedt non era il primo astronomo a trattare serie di questo tipo; il primato spetta cronologicamente a Simon Newcomb, il quale nel 1874 dimostrò che le equazioni differenziali che descrivono il moto dei pianeti possono essere soddisfatte, almeno formalmente, da serie trigonometriche. Tuttavia fu il metodo di Lindstedt ad acquisire grande notorietà, poiché la sua minore complessità lo rendeva adatto a ulteriori generalizzazioni; esso era infatti notevolmente più semplice del metodo di Gyldén, nonostante fosse meno efficace, dal momento che alla maggiore semplicità corrispondeva una restrizione delle possibili applicazioni.
Nella seconda metà degli anni Settanta del XIX sec. apparvero due articoli destinati ad avere un grande effetto, sia sullo sviluppo della meccanica celeste in generale sia in particolare sul problema dei tre corpi. Nel 1877 l'astronomo e matematico americano George W. Hill (1838-1914) pubblicò uno straordinario articolo sul moto del perigeo lunare, che conteneva ‒ per la prima volta dalla scoperta di soluzioni periodiche particolari effettuata da Lagrange nel 1772 ‒ nuove soluzioni periodiche del problema dei tre corpi. L'anno dopo Hill pubblicò un articolo sulla teoria lunare in cui esponeva una deduzione più dettagliata delle soluzioni periodiche e in cui si evidenziava l'importanza dell'integrale di Jacobi nell'individuare le regioni del moto del pianetino. Le idee di Hill furono un primo importante stimolo per Poincaré, soprattutto per la teoria che questi avrebbe sviluppato sulle funzioni periodiche.
Gli studi di Poincaré
L'interesse di Poincaré per il problema dei tre corpi e per la stabilità del Sistema solare fu evidente fin dagli inizi della sua carriera. Fu tale problema, in particolare, che lo portò a concepire la pionieristica memoria sulla teoria qualitativa delle equazioni differenziali, pubblicata tra il 1881 e il 1886 in una serie di quattro articoli, in cui cercava di studiare geometricamente il comportamento globale della famiglia di curve-soluzioni di un'equazione differenziale. L'idea di rappresentare le soluzioni di un'equazione differenziale in termini di curve piuttosto che di funzioni segnò un importante distacco dai suoi predecessori, i quali, nelle loro ricerche, avevano utilizzato prevalentemente metodi di sviluppo in serie di potenze. In quei quattro articoli, caratterizzati dal risalto dato agli aspetti geometrici e dall'attenzione prestata alle variabili reali in quanto contrapposte alle variabili complesse, Poincaré discusse per la prima volta il problema della stabilità, sviluppando gran parte di quella teoria che avrebbe usato, in seguito, proprio per affrontare il problema dei tre corpi.
Parallelamente al lavoro sulle equazioni differenziali, il matematico francese studiò anche le serie utilizzate dagli astronomi e, a partire da un saggio pubblicato nel 1882, indagò la convergenza della serie trigonometrica generale della forma
[3] ∑Ansenαnt+∑Bncosαnt,
dove gli αn non sono proporzionali a coefficienti interi. Si tratta di serie molto diverse da quelle di Fourier, che possono crescere o decrescere indefinitamente. Il loro uso in meccanica celeste poneva il problema di studiarne la convergenza. Poincaré inizialmente si soffermò sulla distinzione tra convergenza assoluta e convergenza uniforme e dimostrò che, se la convergenza non è uniforme, allora la funzione può crescere indefinitamente. Si trattava di un risultato importante perché implicava che, contrariamente a quanto gli astronomi avevano creduto, per dimostrare la stabilità del Sistema solare non bastava che le distanze reciproche tra i vari corpi fossero rappresentate mediante serie trigonometriche convergenti: occorreva infatti che la convergenza fosse uniforme. Poincaré studiò dettagliatamente anche le serie di Gyldén e di Lindstedt e, oltre a dimostrare la divergenza di quest'ultima, ottenne una loro nuova derivazione ricorrendo alla teoria di Hamilton-Jacobi.
Il primo articolo che Poincaré scrisse sul problema dei tre corpi, pubblicato nel 1884, conteneva una trattazione delle soluzioni periodiche; su tale articolo si basarono le successive ricerche del matematico francese circa le proprietà di soluzioni rappresentate da curve chiuse, che egli trattò nel quarto dei suoi articoli sulla teoria qualitativa delle equazioni differenziali; in esso considerò il caso in cui due dei tre corpi avessero massa molto più piccola del terzo. Poincaré dimostrava che era possibile scegliere le condizioni iniziali in modo che le distanze reciproche tra i corpi fossero funzioni periodiche del tempo, provando così l'esistenza di un'infinità continua di soluzioni periodiche e ottenendo una generalizzazione del risultato di Hill. Poincaré mostrò che vi sono tre specie di soluzioni periodiche, a seconda della natura dei moti a due corpi che le generano:
1) quelle nelle quali le inclinazioni sono nulle e le eccentricità molto piccole (le soluzioni periodiche di Hill erano di questo tipo) ‒ generate nel caso di orbite a due corpi di tipo circolare;
2) quelle in cui le inclinazioni sono nulle e le eccentricità finite ‒ generate nel caso di orbite a due corpi di tipo ellittico;
3) quelle in cui le inclinazioni sono finite e le eccentricità molto piccole ‒ generate da orbite a due corpi circolari e tali che l'inclinazione del terzo corpo rispetto al piano del moto dei due primari è diversa da zero.
Poincaré immaginò anche che potesse esistere un quarto tipo di soluzione periodica, nel caso in cui sia le inclinazioni sia le eccentricità fossero finite, ma riuscì a dimostrarne l'esistenza soltanto nel caso in cui il rapporto tra le due masse più piccole assumesse alcuni valori particolari.
Anche se la probabilità che tali soluzioni si presentino effettivamente è praticamente nulla (in quanto la loro esistenza dipende da particolari valori dei dati iniziali), Poincaré comprese che la loro importanza risiedeva nella possibilità di interpretarne il legame con altre soluzioni a esse vicine. Egli osservò che, se le condizioni iniziali erano molto vicine a quelle di una soluzione periodica, allora la soluzione effettiva poteva essere considerata come una perturbazione di quella periodica. Nell'ipotesi che le perturbazioni, dello stesso ordine delle inclinazioni e delle eccentricità, fossero tanto piccole da poter trascurare i loro quadrati, Poincaré mostrò che le differenze tra orbite vere e orbite periodiche potevano essere espresse da serie trigonometriche prive di termini secolari. Ciò ridusse notevolmente l'errore derivante dall'applicazione del metodo generale, che comportava la variazione secolare delle eccentricità.
Nel 1890 Poincaré pubblicò la famosa monografia sul problema dei tre corpi (Sur le problème des trois corps et les équations de la dynamique), dopo una vicenda che durò circa cinque anni. Nel luglio del 1885 era apparso l'annuncio di un importante concorso internazionale di matematica, patrocinato dal re di Svezia e Norvegia Oscar II per festeggiare il suo sessantesimo compleanno, che sarebbe avvenuto nel 1889. L'organizzazione della gara fu affidata al matematico svedese Gustaf Mittag-Leffler; questi avrebbe anche fatto parte della giuria, composta inoltre da Karl Theodor Wilhelm Weierstrass di Berlino e da Charles Hermite di Parigi. Furono poste quattro questioni, una delle quali chiedeva di fornire una soluzione, espressa per mezzo di una serie di potenze convergente, al problema degli n corpi, nel caso privo di collisioni. Il quesito era stato suggerito da Weierstrass e rifletteva l'interesse che da tempo questi nutriva per tale argomento.
I termini nei quali Weierstrass aveva formulato la questione traevano origine da sue ricerche e da considerazioni effettuate precedentemente da Peter Gustav Lejeune Dirichlet (1805-1859). Nel 1858, infatti, Dirichlet aveva riferito a Leopold Kronecker, suo studente, di aver scoperto un nuovo metodo generale per l'integrazione delle equazioni differenzia-li della meccanica; applicando questo metodo era riuscito a dimostrare la stabilità del Sistema solare. Sfortunatamente Dirichlet morì poco tempo dopo quella confidenza, senza lasciare alcuna traccia scritta della sua scoperta. In una lettera a Mittag-Leffler dell'agosto del 1878, Weierstrass rivelò di aver ottenuto lo sviluppo in serie di potenze delle soluzioni quasi-periodiche del problema degli n corpi, ma confessò di non riuscire a provarne la convergenza. Per quanto vani fossero i suoi tentativi di dimostrazione, Weierstrass era convinto, soprattutto per le osservazioni di Dirichlet, che le serie convergessero effettivamente. Includendo quel problema nella competizione, Weierstrass sperava quindi che si riuscisse a ottenere il metodo di Dirichlet.
Poincaré aveva deciso di affrontare il problema degli n corpi partendo da quello generale dei tre corpi, con l'idea di estenderne poi i risultati; tuttavia le difficoltà intrinseche lo costrinsero a concentrarsi quasi esclusivamente sul secondo e più circoscritto di essi. Pur non avendo risolto il problema degli n corpi, il lavoro del matematico francese fu giudicato eccezionale e nel gennaio del 1889 Poincaré ricevette il premio. L'anno seguente fu pubblicata la sua monografia sul problema dei tre corpi, come spettava al vincitore del concorso.
La fortunata combinazione tra l'alto patrocinio del re e una ben organizzata campagna di pubbliche relazioni fece sì che il concorso ottenesse l'insolito privilegio di acquisire notorietà anche al di fuori del mondo matematico. Nei numerosi necrologi e commenti sull'opera di Poincaré, non soltanto quella monografia spicca per le lodi che raccoglie, ma spesso si puntualizza come la vincita del concorso indetto dal re Oscar assicurò ampia notorietà al nome del matematico francese. In seguito quel saggio è divenuto famoso sia perché costituisce la base del celebre lavoro in tre volumi sulla meccanica celeste, Les méthodes nouvelles de la mécanique céleste (1892-1899), sia perché contiene la prima descrizione matematica del comportamento caotico di un sistema dinamico.
Oggi tuttavia sappiamo che questa monografia tanto apprezzata è in realtà molto diversa dalla versione a cui venne effettivamente conferito il premio. Nell'introduzione della versione data alle stampe, Poincaré riconosceva sì di aver ritoccato il lavoro per la pubblicazione, ma non indicava in alcun modo la natura e la portata di quelle modifiche. La scoperta di una versione stampata e annotata dall'autore stesso ha rivelato però la vera consistenza di quella revisione, mostrando come nella versione originale non vi fosse traccia di alcuni dei principali risultati che oggi hanno reso famoso quel lavoro. Cosa ancor più importante, essa ha evidenziato come i nuovi risultati ottenuti da Poincaré non fossero semplici estensioni dei precedenti, ma fossero dovuti piuttosto alla scoperta, soltanto pochi giorni prima del termine utile per la pubblicazione del saggio, di un errore significativo. Questa scoperta costrinse Poincaré a riscrivere gran parte del lavoro, attività, questa, che ritardò non poco la pubblicazione. Anche se la presenza dell'errore era nota ad alcuni dei suoi contemporanei, le sue conseguenze sono state comprese solamente di recente; che si trattasse di un errore significativo è evidente: fu proprio nel tentativo di correggerlo infatti che Poincaré scoprì il fenomeno del caos.
Naturalmente la scoperta di quell'errore lo turbò e lo indusse persino a dubitare che il suo saggio fosse meritevole di essere premiato. Sebbene non ci fosse alcuna intenzione di privarlo del premio, Poincaré dovette pagare personalmente la ristampa del saggio e sostenere così una spesa ben superiore all'entità del premio vinto.
Il concorso stimolò Poincaré a sintetizzare molte delle idee che aveva sviluppato nei dieci anni precedenti. Nel saggio affrontava il problema adottando un nuovo approccio qualitativo, ben diverso e certamente molto più efficace di tutte le precedenti metodologie. Il matematico francese attribuiva la massima importanza alle soluzioni periodiche, la cui trattazione teorica, basata su sue ricerche precedenti, costituisce il cuore della monografia.
Nel formulare il problema ristretto, egli descrisse la posizione del pianetino nello spazio delle fasi mediante due variabili di posizione e due variabili angolari, rispettivamente x1,x2,y1,y2, legate tra loro dall'integrale della conservazione dell'energia, F(x1,x2,y1,y2)=C. Poincaré espresse le equazioni differenziali in forma canonica,
e le considerò, in base alla teoria qualitativa da lui sviluppata precedentemente, generatrici di flussi su una superficie tridimensionale. La sua intuizione geniale fu rendersi conto che, invece di considerare il flusso in tutto lo spazio tridimensionale, di gran lunga più conveniente era studiare l'applicazione (oggi nota come 'mappa di Poincaré di primo ritorno') prodotta dal flusso su una superficie bidimensionale di area S perpendicolare al flusso stesso. Tale mappa è definita in modo tale da associare a ogni punto M, intersezione di S con una linea del flusso, il punto M′, in cui quella linea di flusso torna a incontrare S. Così, mentre nello spazio tridimensionale una soluzione periodica corrisponde a una curva chiusa, nella mappa di primo ritorno una soluzione periodica di periodo 2π corrisponde a un punto fisso e una soluzione con periodo 2kπ corrisponde a un ciclo di periodo k.
Per esprimere in serie di potenze la soluzione dell'equazione, Poincaré usò come parametro la massa μ del più piccolo tra i due corpi primari. Questo perché, se μ=0, il problema si riduce a una coppia di problemi a due corpi e quindi, per valori piccoli di μ, è possibile considerare il problema come una perturbazione di quello a due corpi. Proseguì dunque usando il metodo della continuazione analitica per vedere se esistessero soluzioni per valori molto piccoli di μ.
Sviluppò l'hamiltoniana F in serie di potenze di μ,
[5] F=F0+ μF1+μ2F2 +…,
ipotizzando che per μ=0 esistessero soluzioni periodiche della forma
[6] xi=φi(t), yi=ψi(t).
Quindi mostrò che esistevano anche soluzioni periodiche della forma
[7] xi=φi(t)+Siexp(αkt), yi=ψi(t)+Tiexp(αkt),
dove Si e Ti sono funzioni periodiche di t e αk sono particolari costanti che egli chiamò 'esponenti caratteristici'. Poincaré si rese conto di un fatto fondamentale: la stabilità delle soluzioni dipende dalla forma degli esponenti caratteristici; se questi sono tutti immaginari, allora la soluzione periodica è stabile, altrimenti è instabile. Nelle trattazioni della stabilità, Poincaré usò la definizione proposta da Poisson, considerando stabile il moto di un punto se esso ripassava infinite volte in posizioni arbitrariamente vicine alla sua posizione iniziale.
La teoria delle soluzioni periodiche di Poincaré produsse numerosi risultati importanti. Essa lo portò non soltanto a scoprire tipi particolari di soluzioni periodiche, ma anche a formulare la famosa congettura sulla densità delle soluzioni periodiche: data una qualsiasi soluzione particolare del problema ristretto, dovrebbe essere possibile trovare una soluzione periodica (che potrebbe anche avere un periodo estremamente lungo) tale che per ogni intervallo di tempo assegnato la differenza tra le due sia arbitrariamente piccola, purché nel sistema non si verifichino né fughe né collisioni. Poincaré non fornì una dimostrazione rigorosa della congettura, che fu provata da Eberhard Hopf nel 1930.
Oltre a essere di per sé più facili da studiare, le soluzioni periodiche stabiliscono un punto di partenza naturale per lo studio e la classificazione di altre soluzioni, in particolare per quelle che si avvicinano arbitrariamente a esse. Poincaré seppe intuire queste potenzialità e, studiando soluzioni che differivano di poco da quelle periodiche, giunse all'importante scoperta delle soluzioni asintotiche, vale a dire delle soluzioni che per t →+∞ o per t →−∞ si avvicinano lentamente a una soluzione periodica instabile. Da un punto di vista fisico, dopo un lungo intervallo di tempo una soluzione asintotica o diventa praticamente indistinguibile dalla soluzione periodica che l'ha generata, oppure ne diverge con continuità. Poincaré si interessò particolarmente al caso in cui a una stessa soluzione periodica sono associati entrambi i tipi di soluzioni asintotiche. Egli mostrò che nello spazio tridimensionale delle soluzioni del problema ristretto le soluzioni asintotiche generano famiglie di curve; queste riempiono superfici e approssimano asintoticamente la curva che rappresenta la soluzione periodica data. In termini di mappa di primo ritorno, se si rappresenta la soluzione periodica con un punto P sulla sezione trasversale e si itera successivamente la mappa, i punti che si avvicinano a P asintoticamente per t →+∞ formano ciò che oggi chiamiamo varietà stabile, mentre quelli che si avvicinano asintoticamente a P per t →−∞ formano una varietà instabile. È possibile in tal modo far corrispondere le superfici asintotiche a curve stabili e instabili sulla sezione trasversale.
Per comprendere il comportamento di tali soluzioni asintotiche, Poincaré cercò di ricavare le equazioni esatte delle superfici asintotiche (sotto forma di serie infinite sviluppate secondo le potenze del parametro μ), partendo dalle curve e procedendo per approssimazioni successive. Questa indagine richiese lo sviluppo di quello che sarebbe diventato un altro importante argomento del saggio, particolarmente significativo per l'errore compiuto: la teoria degli integrali invarianti.
Sebbene Poincaré non sia stato il primo a riconoscere l'esistenza e l'importanza degli integrali invarianti ‒ questi si incontrano già nell'opera di Joseph Liouville (1809-1882) e di Ludwig Boltzmann (1844-1906) ‒ fu lui a sviluppare la teoria generale, grazie alla quale si comprese che l'esistenza di un integrale invariante è una proprietà fondamentale delle equazioni differenziali di Hamilton. La teoria degli integrali invarianti lo portò anche a formulare il teorema della ricorrenza: data una regione comunque piccola dello spazio delle fasi, esistono sempre traiettorie che la attraversano infinite volte. Ciò equivale a dire che, in qualche istante futuro, il sistema tornerà arbitrariamente vicino alla sua situazione iniziale, e ciò si ripeterà infinite volte. Da tale risultato Poincaré ricavò che, date certe condizioni iniziali, esistono infinite soluzioni del problema ristretto che risultano stabili secondo Poisson e dedusse che le altre soluzioni possono essere considerate eccezionali. Questo teorema ebbe in seguito un ruolo fondamentale nella formulazione della teoria ergodica.
Poincaré concluse la sua discussione sugli integrali invarianti con una serie di teoremi e fu proprio in uno di questi che commise l'errore cruciale della sua concezione geometrica. Il matematico pensava infatti di aver dimostrato che una curva era chiusa quando in realtà, come si accorse in seguito, essa intersecava sé stessa; in sostanza egli non aveva preso in considerazione tutte le possibilità compatibili con i vincoli imposti dall'esistenza dell'integrale invariante. Ciò lo condusse ad affermare erroneamente che le intersezioni delle superfici asintotiche con la sezione trasversale fossero rappresentate da curve chiuse, e quindi che le stesse superfici asintotiche fossero chiuse. Per di più, tale risultato implicava la stabilità, nel senso che le soluzioni restavano confinate in una data regione dello spazio. Poincaré credeva di aver dimostrato che, per valori sufficientemente piccoli del parametro μ, vi fosse, rispetto a una data soluzione periodica instabile, un insieme di soluzioni asintotiche che potevano essere considerate stabili, che tali soluzioni avessero un comportamento regolare e che potessero essere interpretate.
L'errore si ripercosse anche nella sua descrizione analitica delle soluzioni asintotiche. Nel calcolare inizialmente gli sviluppi in serie, Poincaré aveva infatti assunto che questi fossero convergenti. Tale calcolo costituiva tuttavia un compito delicato, reso difficile dai problemi di convergenza originati dai piccoli divisori; Poincaré stesso avrebbe in seguito scoperto che le serie erano di fatto divergenti.
Nella versione riveduta e corretta del saggio, l'autore in primis mostrò che le serie delle soluzioni asintotiche non convergevano, ma appartenevano a quella famiglia di serie oggi note come 'serie asintotiche', delle quali lui stesso aveva dato la prima definizione formale nel 1886. Stabilì poi che le curve stabili e instabili che rappresentavano le superfici asintotiche sulla sezione trasversale non erano chiuse, ma si intersecavano trasversalmente; il punto di intersezione dava luogo a un nuovo tipo di soluzione, che chiamò 'doppiamente asintotica' (e più tardi 'soluzione omoclina'). Inoltre scoprì che, dall'esistenza di una soluzione doppiamente asintotica, scaturiva quella di infinite altre. Egli capì che la presenza di siffatte soluzioni implicava non soltanto l'instabilità, ma un comportamento di una complessità sconcertante. Questo tipo di moto è oggi detto 'caotico'. Le soluzioni stabili e instabili si incrociano infinite volte formando un groviglio che Poincaré non provò nemmeno a disegnare. Anche se non dedicò grande attenzione al comportamento caotico da lui stesso scoperto, Poincaré ne rimase profondamente turbato e passarono quasi dieci anni prima che tornasse a pubblicare qualcosa di nuovo sull'argomento.
Oltre alla scoperta del comportamento caotico, il saggio conteneva qualche altro risultato importante, come per esempio la dimostrazione della non esistenza di nuovi integrali per il problema ristretto. Questo confermò il risultato ottenuto nel lavoro pubblicato nel 1887 da Ernst Heinrich Bruns, in cui egli dimostrava che, nel problema generale dei tre corpi, non potevano esistere altri integrali algebrici oltre a quelli già noti. Il saggio trattava inoltre le serie di Lindstedt, dimostrando che esse non convergevano uniformemente per tutti i valori delle costanti arbitrarie di integrazione. Le conclusioni a cui Poincaré era arrivato, anche se non del tutto complete ‒ non prendevano in considerazione ipotesi capaci di garantire la convergenza ‒, sembrarono effettivamente vanificare le speranze che avevano indotto Weierstrass a porre il problema.
I tre volumi riguardanti Les méthodes nouvelles de la mécanique céleste di Poincaré contenevano le stesse idee principali della monografia premiata, ma in forma ancora più esplicita e più completa. Vi si trovava un numero maggiore di applicazioni della teoria, oltre a una notevole quantità di nuovi argomenti, e si poneva attenzione tanto al problema generale dei tre corpi quanto a quello ristretto. Il primo volume conteneva una estesa trattazione delle soluzioni periodiche e asintotiche e della non esistenza di nuovi integrali uniformi. Il secondo volume era dedicato ai metodi perturbativi di Newcomb, Gyldén, Lindstedt e Bohlin e alle loro applicazioni al problema dei tre corpi. Nell'ultimo volume, dominato dalle idee geometriche di Poincaré, venivano infine discussi gli integrali invarianti e la stabilità e qui l'autore tornava, per la prima volta, sulle soluzioni doppiamente asintotiche. Sviluppando ulteriormente la teoria, egli scoprì un nuovo tipo di soluzione, persino più complesso del precedente; denominò 'eteroclina' tale soluzione in quanto, a differenza di quella omoclina, era associata non a una, ma a due diverse soluzioni periodiche instabili ed era perciò ancor più complicata.
Poincaré pubblicò anche articoli di natura generale sul problema dei tre corpi e sulla stabilità del Sistema solare; tali articoli aprivano prospettive più ampie e concrete di quelle che avevano caratterizzato il lavoro del 1890 e fornivano una risposta adeguata a chi auspicava una presentazione maggiormente divulgativa delle sue idee. Nel primo articolo (Poincaré1891a) l'autore fornì un sunto della monografia del 1890, con il preciso scopo di renderla accessibile agli astronomi e a chiunque fosse interessato per scopi pratici al problema dei tre corpi. Nell'articolo successivo (Poincaré 1891b) i risultati sul problema ristretto dei tre corpi erano esposti in modo quasi del tutto descrittivo, mentre la relazione tra i risultati matematici e il problema fisico della stabilità del Sistema solare era appena sfiorata; i concetti erano illustrati con l'aiuto di esempi, senza far uso di formule matematiche.
In Sur la stabilité du système solaire, che apparve nel 1898, Poincaré ripercorse brevemente (ma in modo leggermente impreciso) la storia di alcune precedenti dimostrazioni della stabilità, come quelle fornite da Lagrange e Poisson. Egli discusse anche i limiti insiti nel rappresentare il Sistema solare come un insieme di punti materiali soggetti esclusivamente all'attrazione gravitazionale reciproca.
Nel riconoscere che i corpi reali sono soggetti ad altre forze oltre quella gravitazionale, egli si interrogò sulla natura e sull'entità di quelle che chiamò 'forze complementari'. Osservò, infatti, che se si fosse riusciti a dimostrare che l'effetto complessivo di tali forze era in realtà maggiore di quello dovuto ai termini trascurati nelle approssimazioni usate per provare teoricamente la stabilità, allora si sarebbe potuto legittimamente ignorare il grado d'accuratezza perso nell'approssimare. In sostanza Poincaré si chiedeva se la stabilità fosse più facilmente compromessa dalle forze complementari oppure dall'attrazione gravitazionale stessa.
Nel cercare una risposta, si concentrò sul problema della discordanza tra quanto prevedeva la legge di Newton dell'inverso del quadrato e quanto si osservava sperimentalmente nella precessione del perielio di Mercurio (una delle questioni risolte in seguito dalla teoria della relatività generale di Einstein). Egli osservò che, dal punto di vista della stabilità, qualsiasi altra legge, abbastanza simile a quella dell'inverso del quadrato, avrebbe potuto essere considerata equivalente e non avrebbe avuto alcuna influenza sul risultato finale. Poincaré indicò anche un'altra ragione, ben più stringente, che si opponeva alla stabilità: la seconda legge della termodinamica, in base alla quale vi è una continua dissipazione di energia meccanica in energia termica. Egli ipotizzò che nella dinamica celeste ciò si manifestasse sia nell'incessante azione delle maree ‒ presente anche nei corpi solidi, mai perfettamente elastici ‒ sia nelle forze generate dai campi magnetici dei corpi. Dopo aver esaminato tali forze, egli concluse che sebbene la dissipazione che ne conseguiva fosse estremamente lenta, tuttavia, essa avveniva a una velocità sufficiente a produrre una perturbazione maggiore di quella dovuta ai termini trascurati nell'approssimazione adottata per dimostrare teoricamente la stabilità. In altri termini, Poincaré riteneva che l'accuratezza della dimostrazione teorica avesse raggiunto dei limiti oltre i quali non vi era più un'utilità pratica, senza con questo voler sminuire l'interesse o il valore di ulteriori ricerche sul problema puramente teorico.
Regolarizzazione nel problema dei tre corpi
Nel quesito posto nella gara patrocinata dal re Oscar, si ipotizzava che non vi fossero collisioni tra i corpi e Poincaré, nella sua analisi, si attenne a tale presupposto. Tuttavia, se si fosse voluto ottenere una soluzione completa del problema dei tre corpi, allora si sarebbe dovuto tener conto anche di possibili collisioni. Poiché una collisione corrisponde a una singolarità nelle equazioni differenziali, nasceva il problema della regolarizzazione: ci si chiedeva se sarebbe stato possibile, con un cambio della variabile indipendente, eliminare le singolarità, in modo tale da poter seguire il moto del sistema anche dopo la collisione. Da questa domanda ne scaturiva un'altra, sulla natura delle singolarità: sarebbero potute esistere altre singolarità, che non derivavano da collisioni?
Nel 1896 Paul Painlevé (1863-1933) dimostrò che le uniche singolarità possibili erano quelle dovute alle collisioni; la vera importanza del suo lavoro è tuttavia l'aver dimostrato che le equazioni che descrivono il moto del problema dei tre corpi si potevano esprimere come serie di potenze convergenti (fondamentalmente simili a serie di Taylor), purché le condizioni iniziali fossero tali da escludere un urto tra due o tre corpi in un tempo finito. In altri termini, sarebbe stato possibile trovare una soluzione al problema dei tre corpi se si fosse riusciti a stabilire con precisione le condizioni iniziali che portavano a collisioni. Painlevé immaginò che tali condizioni dovessero soddisfare due relazioni analitiche distinte (che si sarebbero ridotte a una nel caso di moto su uno stesso piano). In seguito, dopo aver generalizzato il teorema di Bruns sull'esistenza di integrali algebrici per il problema dei tre corpi, dimostrò che le relazioni dovevano essere trascendenti, ma non riuscì a compiere ulteriori sviluppi. Nel problema degli n corpi, Painlevé trovò inoltre una condizione sufficiente affinché una singolarità fosse un urto, ma non riuscì a risolvere il problema dell'esistenza o meno di singolarità che non fossero urti nel caso n≥4.
Nel 1903 Tullio Levi Civita (1873-1941) caratterizzò le traiettorie singolari del problema ristretto, trovando le relazioni analitiche previste da Painlevé. Un ricercatore dell'Università di Roma, Giulio Bisconcini, diede un ulteriore contributo ricavando, nel 1906, due distinte relazioni analitiche tra le condizioni iniziali, che, se soddisfatte, indicavano l'esistenza di un urto entro un tempo finito. La sua soluzione non era del tutto soddisfacente, in quanto coinvolgeva una complicata serie infinita e poteva essere applicata direttamente soltanto nel caso in cui il tempo trascorso tra l'istante iniziale e l'urto fosse stato abbastanza breve, criterio per il quale egli non specificò alcuna condizione. Infine né Levi Civita né Bisconcini studiarono il caso di collisioni triple.
Nel 1907 un astronomo dell'Osservatorio di Helsinki, Karl Sundman (1873-1959), descrisse in modo completo le condizioni iniziali che conducevano sia a urti binari sia a urti tripli, fornendo così la soluzione prevista da Painlevé. Nel caso di una collisione binaria Sundman introdusse una nuova variabile ω‚ che sostituiva il tempo t in modo tale che sia t sia le coordinate q restassero funzioni regolari di ω durante la collisione dei due corpi. Quindi trovò alcuni sviluppi di t e q in serie di potenze di ω, capaci di descrivere l'intero moto. Egli dimostrò che un urto triplo sarebbe potuto avvenire solamente nel caso in cui fosse stato nullo il momento della quantità di moto, stabilendo inoltre che tre corpi, nell'avvicinarsi alla collisione, tendevano ad assumere asintoticamente o una configurazione collineare o una a triangolo equilatero. Oltre all'importanza dei risultati conseguiti da Sundman, stupisce la semplicità dei metodi con i quali li ottenne: si trattava essenzialmente di applicare un'estensione del ben noto teorema di Cauchy sull'esistenza di soluzioni di equazioni differenziali. Sundman aveva quindi fornito una dimostrazione a un problema che, sin dalla pubblicazione dei Principia di Newton, era stato oggetto della ricerca di molti grandi matematici e astronomi.
Nonostante l'importanza della scoperta di Sundman fosse stata certamente riconosciuta dai suoi contemporanei, l'interesse per il suo lavoro non durò a lungo e, nel giro di dieci anni, cadde quasi completamente nell'oblio. Ciò accadde per due ragioni. In primo luogo le limitazioni pratiche dei suoi risultati: le serie che aveva ottenuto convergevano assai lentamente ‒ per determinare il moto delle particelle anche solamente per un periodo di tempo estremamente breve è necessario sommare diversi milioni di termini ‒, tanto che, ai fini pratici, risultavano più utili le classiche serie divergenti. In secondo luogo, i risultati ottenuti da Sundman non davano alcuna informazione qualitativa sulla natura del moto. Egli aveva sì fornito una soluzione, ma non tale da rivelare informazioni generali sulla forma delle traiettorie. Così, anche se aveva trovato una soluzione espressa come serie di potenze convergente e valida per un qualsiasi intervallo di tempo, Sundman aveva lasciato irrisolto un gran numero di questioni connesse.
Teoria generale della stabilità
Il problema della stabilità del Sistema solare costituiva un argomento centrale nelle indagini scientifiche di Poincaré. Egli aveva infatti discusso per la prima volta la stabilità delle soluzioni di equazioni differenziali nel 1885, in un periodo in cui si dedicava anche allo studio della stabilità delle diverse forme assunte da masse di fluido rotanti, un lavoro che costituì il primo legame tra la sua opera e quella del matematico russo Aleksander Ljapunov (1857-1918).
Ljapunov era impegnato anche nello studio degli aspetti qualitativi della teoria della stabilità. Le sue ricerche furono pubblicate due anni dopo la loro conclusione, in un'importante monografia del 1892; era il primo tentativo di creare una teoria interamente matematica che descrivesse la stabilità di un sistema di n corpi in movimento. Sfortunatamente quella memoria fu pubblicata in russo e ciò la rese quasi del tutto inaccessibile alla comunità scientifica. Solo nel 1907, con la pubblicazione di una traduzione in francese, le idee di Ljapunov iniziarono a farsi strada nel mondo matematico occidentale e si riconobbe che il suo studio della stabilità costituiva un'importante integrazione di quello di Poincaré.
Ljapunov, pur riconoscendo apertamente l'influenza delle idee del matematico francese sulle proprie ricerche, diede una definizione di stabilità molto più forte di quella adottata da Poincaré. Egli definì stabile la soluzione di un sistema di equazioni differenziali se altre soluzioni, che in un istante dato si trovano abbastanza vicine alla soluzione data, vi rimangono arbitrariamente vicine per tutto il tempo che segue. Ciò significa che, se una soluzione è stabile nel senso di Ljapunov, non soltanto il moto perturbato non può deviare di molto da quello non perturbato, ma ciascun punto del moto perturbato deve essere, in ogni istante, sufficientemente vicino al punto che, nello stesso istante, si trova sulla traiettoria non perturbata. Questa condizione è più vincolante della stabilità di Poisson, che prevede solamente che restino vicine le curve tracciate nello spazio delle fasi, senza richiedere soluzioni che restino vicine nel tempo.
Pur essendoci molte analogie tra i risultati ottenuti da Ljapunov e da Poincaré, le diverse definizioni di stabilità che essi adottarono fecero sì che le loro analisi seguissero indirizzi profondamente diversi. Il campo di applicazione della teoria di Ljapunov, pur estremamente rigorosa e dettagliata, era circoscritto da una definizione che, in fin dei conti, risultava troppo vincolante. Nella pratica, infatti, poiché sono pochissimi i sistemi dinamici in grado di soddisfare completamente i criteri di Ljapunov, la sua teoria era applicabile solo nell'ambito più ristretto di un'analisi locale. La teoria della stabilità di Poincaré, invece, basandosi su una definizione meno restrittiva, poteva essere applicata a problemi più complessi di quelli trattabili con la teoria di Ljapunov. Poincaré era partito dalla sua teoria degli integrali invarianti, che, unita alla sua definizione di stabilità, gli consentì di affrontare problemi generali di stabilità dei sistemi dinamici: risultati quali il teorema della ricorrenza gli permisero di gettare luce sull'andamento delle soluzioni del problema ristretto dei tre corpi. La sua teoria conduceva quindi a una conoscenza del comportamento globale dei sistemi, risultato impossibile da ottenere nell'ambito ristretto della teoria di Ljapunov, anche se ciò aveva come contropartita l'imprecisione che accompagnava l'analisi locale del moto.
Data l'iniziale inaccessibilità del lavoro del matematico russo, furono le idee di Poincaré a essere notate per prime. Ciononostante la teoria di Ljapunov, essendo anche più adatta a essere ulteriormente generalizzata, fornì un contesto preciso e convenzionale entro cui lavorare ed è quindi universalmente considerata come uno dei risultati fondamentali della teoria qualitativa delle equazioni differenziali. Attorno al lavoro di Ljapunov è cresciuta e continua a svilupparsi una vastissima letteratura, come avviene recentemente nella teoria del controllo.
Anche Levi Civita si occupò della stabilità, ma in modo leggermente diverso. Il suo interesse per la meccanica analitica e per il problema dei tre corpi si univa a un acuto intuito geometrico. Questo connubio tra meccanica e geometria lo portò a considerare una definizione di stabilità che, pur molto simile a quella di Ljapunov, tuttavia ne differiva in un aspetto cruciale. Mentre la definizione di Ljapunov riguardava solamente la stabilità nel futuro, quella di Levi Civita comprendeva sia la stabilità futura sia quella passata, tenendo conto, in tal modo, del principio di reversibilità dei processi fisici. Un altro aspetto importante del lavoro di Levi Civita, che lo distingueva da quello di Ljapunov, era la possibilità di trattare anche il caso in cui l'approssimazione del primo ordine fosse stata insufficiente.
Nel 1901 Levi Civita scrisse un articolo sulla teoria della stabilità, nel quale riportò le idee di Poincaré e di Ljapunov, prestando particolare attenzione al problema ristretto dei tre corpi. Prese in esame un sistema di equazioni differenziali della forma
dove le Xi sono periodiche nel tempo. Egli affermò che la soluzione periodica xi=0 è stabile solamente nel caso in cui in corrispondenza di ogni piccolo intorno E dell'origine (nello spazio delle configurazioni) esiste un altro intorno H tale che, se l'orbita si trova in H inizialmente, allora rimane confinata in E in ogni istante di tempo, sia passato sia futuro. In seguito Levi Civita attribuì il nome di 'stabilità assoluta nel senso di Dirichlet' a questa sua definizione, spiegando che essa derivava dalla definizione classica di equilibrio stabile, interpretata nell'ambito dello spazio delle configurazioni. Nell'applicare la sua teoria al problema ristretto dei tre corpi Levi Civita mostrò che, nel caso di una soluzione periodica in cui i moti medi del pianetino e degli altri due corpi primari sono commensurabili, il moto è instabile ed esistono soluzioni che si avvicinano e che si allontanano dalla soluzione periodica.
Le indagini numeriche
Accanto all'interesse per la ricerca di soluzioni analitiche del problema dei tre corpi, grande attenzione era dedicata anche alle tecniche di integrazione numerica e alle loro applicazioni. In particolare, questi procedimenti erano utilizzati nella ricerca di famiglie di soluzioni periodiche. Il precursore in questo campo fu George H. Darwin (1845-1912) che, con notevole successo, vi dedicò molti anni del proprio lavoro. L'opera di Darwin è importante non soltanto perché riprendeva direttamente le idee di Poincaré e di Hill, ma anche perché poneva le basi di un'attività che è ai giorni nostri in pieno sviluppo. Infatti, mentre gli analisti numerici alla fine del XIX sec. erano costretti a operazioni lunghe e laboriose, attualmente la possibilità di disporre di potenti elaboratori elettronici fa sì che integrare numericamente sia spesso un modo relativamente veloce nonché efficiente di sondare un problema dinamico complesso.
In un articolo del 1897, Darwin trattava il calcolo numerico delle soluzioni periodiche del problema ristretto dei tre corpi assieme alla discussione della loro stabilità. In questo scritto egli ricavava le equazioni del moto usando una formulazione in cui S, il più grande tra i due corpi primari, era posto nell'origine di un sistema di coordinate che ruotava in modo solidale con il secondo corpo primario J, mentre il pianetino P si muoveva nel piano dell'orbita di J. Risolvendo le equazioni del moto egli ottenne l'integrale di Jacobi
[9] V2=2Ω-C,
dove V è la velocità angolare del pianetino, Ω è il potenziale totale del sistema, compreso quello dovuto alla rotazione, e C è la costante di Jacobi determinata dalle condizioni iniziali. Darwin poi, così come già aveva fatto Hill, classificò le varie regioni dello spazio a seconda del valore di C.
Se il moto è reale, e quindi V2>0, allora 2Ω>C e la famiglia di curve 2Ω=C (curve di Hill a velocità nulla) individua le regioni dello spazio entro le quali resta in qualche modo circoscritta la traiettoria del pianetino. Quelle stesse curve costituiscono il luogo dei punti nei quali i tre corpi si muovono, per un istante, come parti di un unico corpo rigido. Usando un rapporto di 10:1 tra le masse dei due corpi primari, Darwin classificò le possibili orbite periodiche a seconda del valore di C (considerato in un intervallo di variabilità limitato) e concluse che la traiettoria passava per quattro stadi critici, che gli permisero di trarre alcune conseguenze sulla stabilità. Poiché era difficile individuare orbite periodiche che effettuassero più di una rivoluzione attorno a entrambi i corpi primari (o attorno a un qualsiasi altro punto dello spazio), Darwin si limitò alla ricerca di orbite rientranti dopo una sola rivoluzione, anche se queste potevano includere (ed effettivamente includevano) cappi. Inoltre, fino al 1909, egli non considerò l'influenza dei pianeti più esterni e dei moti retrogradi.
All'inizio del XX sec., si svilupparono due centri importanti di elaborazioni numeriche per lo studio di soluzioni periodiche; che diedero notevoli contributi all'analisi quantitativa del problema dei tre corpi. Si trattava delle scuole di Forest Ray Moulton (1872-1952) negli Stati Uniti e di Svante Elis Strömgrem (1870-1947) in Danimarca.
Nelle indagini condotte sul problema ristretto dei tre corpi, sia la scuola di Moulton sia quella di Strömgrem concentrarono la loro attenzione sull'individuazione delle orbite periodiche nel caso in cui i due corpi primari abbiano la stessa massa, una situazione, questa, particolarmente importante nella dinamica stellare.
Sviluppi successivi
Il problema della convergenza delle serie di Lindstedt fu il punto di partenza per alcuni rilevanti sviluppi del XX secolo. Contrariamente a quanto auspicato da Weierstrass, Poincaré aveva mostrato che, tranne casi eccezionali, le serie divergono. Rimaneva però una riserva; Poincaré aveva affermato chiaramente di non aver dato alcuna dimostrazione rigorosa nel caso in cui le frequenze fossero precedentemente fissate. Grazie al lavoro di Andrej Nikolaevič Kolmogorov, Vladimir Arnold e Igorevich Moser, iniziato negli anni Cinquanta del Novecento, sappiamo che in quei casi la maggior parte delle serie formali è in effetti convergente, purché la perturbazione sia sufficientemente piccola. Questi risultati sono la base della teoria KAM (dalle iniziali dei loro cognomi), che fornisce metodi per integrare su periodi di tempo infiniti sistemi hamiltoniani perturbati. Il fatto che la teoria KAM stabilisca in modo definitivo l'esistenza di soluzioni del problema a n corpi come serie di potenze convergenti, dimostra che la fiducia espressa da Weierstrass non era stata mal riposta.
Molti matematici, partendo dallo studio del lavoro di Poincaré sul problema dei tre corpi, hanno ricavato nuovi risultati in altri ambiti. Jacques Hadamard (1865-1963) e George D. Birkhoff (1884-1944) hanno proseguito le ricerche di Poincaré per gli aspetti qualitativi, mentre Ivor Bendixon (1861-1935) si è occupato delle equazioni differenziali ordinarie ed Elie Cartan (1869-1951) ha lavorato sulla teoria degli integrali invarianti.
Infine, nonostante il successo della monografia di Poincaré, appare evidente come, durante i primi anni del XX sec., non sia stato fatto alcun serio tentativo di proseguire nello studio del comportamento delle soluzioni asintotiche dello scienziato francese. Ciò si può attribuire in gran parte alla incapacità di intraprendere un'analisi quantitativa, a causa dell'inadeguatezza delle tecniche di calcolo numerico di allora. L'avvento dei calcolatori consente oggi questa analisi; ciò ha determinato il grande sviluppo della ricerca sui sistemi non lineari e permesso il conseguimento di numerosissimi nuovi risultati. Tutto questo ha consentito, tra l'altro, di svelare i segreti della teoria matematica del caos, le cui radici affondano nella teoria delle soluzioni asintotiche di Poincaré. C'è da dire che, oltre alle difficoltà dei calcoli numerici, anche il comportamento apparentemente casuale di tali soluzioni asintotiche mal si accorda con la visione, risalente a Laplace e a quei tempi comunemente accettata, di un modello deterministico di Universo. Forse, fu in parte anche per questa fiducia in un qualche ordine ultimo che Poincaré non riuscì inizialmente a individuare e riconoscere il comportamento caotico.
Bibliografia
Barrow-Green 1997: Barrow-Green, June, Poincaré and the three body problem, Providence (R.I.), American Mathematical Society; London, London Mathematical Society, 1997.
Gillespie 1997: Gillespie, Charles Coulston, Pierre-Simon Laplace (1749-1827). A life in exact science, with the collaboration of Robert Fox and Ivor Grattan-Guinness, Princeton, Princeton University Press, 1997.
Goroff 1993: Goroff, Daniel L., Henri Poincaré and the birth of chaos theory. An introduction to the English translation of 'Les Méthodes nouvelles de la Mécanique céleste', introduction to: Poincaré, Henri, New methods of celestial mechanics, edited and introduced by Daniel L. Goroff, Woodbury (N.Y.), American Institute of Physics, 1993, 3 v.; v. I, pp. 1-107.
Lovett 1912: Lovett, Edgar O., Generalizations of the problem of several bodies, its inversion, and an introductory account of recent progress in its solution, "Quarterly journal of pure and applied mathematics", 42, 1912, pp. 252-315.
Marcolongo 1919: Marcolongo, Roberto, Il problema dei tre corpi da Newton (1686) ai nostri giorni, Milano, Hoepli, 1919 (1. ed.: 1915).
Moulton 1902: Moulton, Forest Ray, An introduction to celestial mechanics, New York-London, Macmillan, 1902 (altra ed.: New York, Dover, 1970).
Szebehely 1967: Szebehely, Victor, Theory of orbits, New York-London, Academic Press, 1967.
Westfall 1980: Westfall, Richard, Never at rest. A biography of Isaac Newton, Cambridge-New York, Cambridge University Press, 1980.
Wilson 1985: Wilson, Curtis, The great inequality of Jupiter and Saturn. From Kepler to Laplace, "Archive for history of exact sciences", 33, 1985, pp. 15-290.