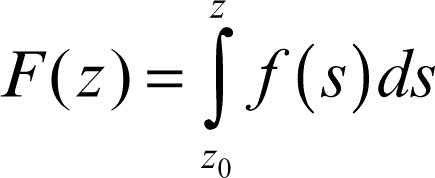integrale complesso

integrale complesso

integrale complesso esteso a una curva regolare C, formalmente ƒ(x + iy) = u(x, y) + iv(x, y), indica la somma dell’integrale esteso a C della forma differenziale udy − vdx e dell’integrale esteso a C della forma differenziale vdx + udy moltiplicato per l’unità immaginaria. Le relative condizioni di integrabilità sono le equazioni di → monogenia. Se ƒ è funzione olomorfa nell’aperto A semplicemente connesso, l’integrale ha un valore che dipende soltanto dai punti estremi della curva. In tali ipotesi, la funzione

con z₀ arbitrario, è olomorfa in A ed è una primitiva di ƒ, ossia F′ (z) = ƒ(z) per ogni z di A; tutte le altre primitive di ƒ si ottengono addizionando a F una costante arbitraria.