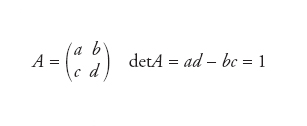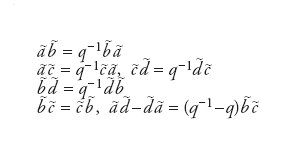gruppi quantistici
gruppi quantistici
Struttura algebrica introdotta e analizzata a partire dagli anni Ottanta del secolo scorso dai matematici russi Ludwig Faddeev e Vladimir Drinfeld e dal giapponese Michio Jimbo. L’idea è quella di costruire una ‘deformazione’ (in un senso opportuno) di algebra di Lie g di un gruppo di Lie G. Nell’approccio di Faddeev il punto di partenza è l’algebra F(G) delle funzioni a valori complessi sul gruppo di Lie G considerato con prodotto commutativo definito da (f1f2)(g)=f1(g)f2(g), g∈G. Quest’algebra può essere dotata della struttura di algebra di Hopf. Per es., nel caso del gruppo SL(2,ℂ) delle matrici complesse 2×2 a determinante unitario
quest’algebra coincide con l’algebra commutativa generata da elementi a∼,b∼,c∼,d∼ soggetti appunto alla relazione a∼d∼−b∼c∼=1. Faddeev considera poi l’algebra Fq(SL(2,ℂ)) generata da simboli a∼,b∼,c∼,d∼ cui è imposta una ‘deformazione’ delle relazioni (per es. ab=ba) che esprimono la loro commutatività:
dove q è un numero complesso differente da zero. La condizione sul determinante delle matrici si trasforma allora in a∼d∼−q−1b∼c∼=1. L’algebra Fq(SL(2,ℂ)) non è isomorfa a F(H) per nessun gruppo H, ma resta comunque un’algebra di Hopf. In accordo con lo spirito della geometria non commutativa, Fq(SL(2,ℂ)) è considerata l’algebra delle funzioni sul gruppo quantistico SLq(2,ℂ). Cosi come SL(2,ℂ) è il gruppo di simmetrie del piano bidimensionale, SLq(2,ℂ) è la simmetria quantistica del piano quantistico, ovvero dell’algebra generata da elementi x,y modulo la relazione xy=qyx. Il piano quantistico è un esempio di spazio non commutativo. Drinfeld e Jimbo considerano invece l’algebra inviluppante U(g) di un’algebra di Lie g. Essendo anch’essa è un’algebra di Hopf, considerano un’opportuna modificazione di prodotto e coprodotto ottenendo l’algebra di Hopf Uq(g). Essa è in senso opportuno il duale dell’algebra Fq(G). La struttura di gruppo quantistico trae origine dallo studio di alcuni modelli (sistemi dinamici) integrabili. Trova oggi applicazione in teoria dei campi e più in generale in fisica matematica.