gioco
gioco
gioco in termini del tutto generali, situazione in cui uno o più soggetti o gruppi di soggetti (i giocatori) debbono seguire delle regole conosciute e condivise per raggiungere un fine. In ogni stadio del gioco (e quindi anche in quello iniziale) eccettuato quello finale, ogni giocatore decide una mossa che modifica lo stato del gioco: l’insieme delle mosse, che possono essere in tutto, in parte o per nulla determinate da fattori casuali, costituisce la strategia. Un gioco le cui mosse siano del tutto casuali (come per esempio il gioco dell’oca) è detto gioco d’azzardo. Ogni gioco termina con un esito per ognuno dei giocatori: la vincita o guadagno, detta anche pay-off. Essa può essere costituita da un punteggio, da una somma in denaro (positiva o negativa, cioè da versare) o dalla semplice proclamazione di vittoria, sconfitta, patta. I giochi possono essere cooperativi (se i giocatori perseguono un fine comune, alcuni di essi possono allearsi: per esempio due aziende che possono essere interessate a formare un duopolio) oppure non cooperativi (nei quali i giocatori non possono stipulare accordi vincolanti). Per i giochi non cooperativi si determina un equilibrio di Nash quando ogni giocatore attua una strategia tale che ogni altra strategia gli farebbe conseguire una vincita minore: J. Nash stesso dimostrò che ogni gioco finito (cioè con un numero di giocatori e di strategie, per quanto miste, finito) ammette un tale equilibrio. Un gioco può inoltre essere a informazione completa se ogni giocatore (come negli scacchi) è a conoscenza di tutte le mosse in ogni stadio del gioco o a informazione parziale (come nel poker). Un gioco è dato in forma estesa se a ogni stadio è noto a chi spetta la mossa successiva, le sue possibili mosse (o le loro eventuali probabilità) e gli esiti finali per ogni possibile conclusione del gioco. Teoricamente, tale tipo di gioco è rappresentabile con un grafo ad albero, che però, anche nel più semplice dei giochi, potrebbe avere dimensioni abnormi a causa dell’enorme numero di strategie possibili. Un gioco è invece in forma normale se sono dati soltanto tutti i singoli esiti in funzione di ogni possibile combinazione di strategie.
Per illustrare i modi in cui si può rappresentare un gioco si può considerare il classico esempio del → dilemma del prigioniero, proposto da A.W. Tucker negli anni Cinquanta del xx secolo:
• due persone A e B sono arrestate perché sospettate di aver commesso un delitto;
• sono detenuti in celle separate e non possono comunicare tra loro;
• ognuno dei due è a conoscenza del fatto che: a) se uno confessa e l’altro non confessa, chi ha confessato viene scarcerato e l’altro è condannato a 7 anni di reclusione; b) se entrambi confessano sono entrambi condannati a scontare 6 anni di reclusione; c) se nessuno confessa sono entrambi condannati a 1 anno.
Entrambi hanno a disposizione due strategie: tacere (T) o confessare (C).
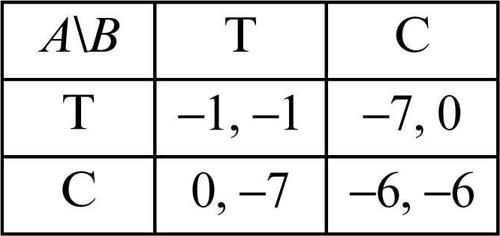
In forma normale il gioco è così rappresentato:
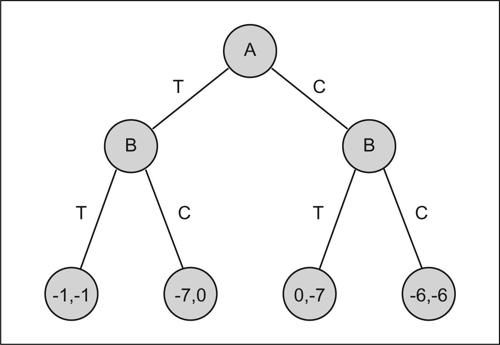
Se i due sospettati non scelgono simultaneamente, ma per esempio sceglie prima A e quindi, conoscendo la scelta di A, sceglie B, il gioco può essere rappresentato in forma estesa con un grafo ad albero (vedi figura).
I giochi maggiormente analizzati da un punto di vista matematico sono, come il precedente, quelli a due persone. In particolare, tra questi ultimi, assumono particolare importanza i giochi a somma zero, in cui cioè la somma algebrica delle vincite è uguale a 0. Se nel gioco le vincite sono associate a fenomeni casuali (e si è quindi di fronte a una variabile aleatoria), si parla di → gioco equo quando la somma algebrica delle vincite moltiplicate per la loro probabilità (detta speranza matematica) è uguale a zero; ripetendo più volte un tale gioco ci si deve aspettare mediamente che la vincita di ciascun giocatore sia uguale a zero (→ giochi, teoria dei).