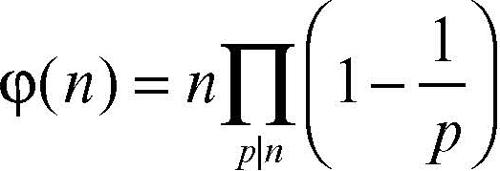Eulero, funzione toziente di
Eulero, funzione toziente di
Eulero, funzione toziente di in teoria dei numeri, fornisce il numero degli interi positivi minori di n che sono coprimi rispetto a n, cioè che non hanno fattori primi comuni con n. È indicata con φ(n), essendo n ∈ N. Per esempio, i numeri minori di 20 che sono coprimi con 20 sono 1, 3, 7, 9, 11, 13, 17,19, per cui φ(20) = 8. Se p è primo, allora φ(p) = p − 1. Se n = pm, allora φ(n) = φ(pm) = pm(1 − 1/p).
Nel caso generale, poiché φ è moltiplicativa, cioè φ(n1n2) = φ(n1)φ(n2) se n1 e n2 sono primi tra loro, risulta
dove il prodotto è esteso a tutti i numeri primi che dividono n. La lunghezza del periodo della frazione 1/n è data da φ(n) o da un suo sottomultiplo (→ Eulero-Fermat, teorema di).