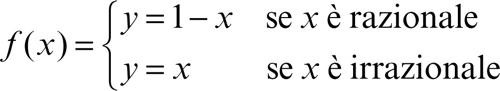funzione inversa

funzione inversa

funzione inversa di una funzione iniettiva ƒ: X → Y, è la funzione, indicata con ƒ⁻¹: Y → X, tale che x = ƒ⁻¹(y) se e solo se y = ƒ(x). Una funzione per la quale è definibile l’inversa è detta invertibile. Se la funzione ƒ, iniettiva, è anche suriettiva, i due insiemi X e Y sono in corrispondenza biunivoca. Se oltre ƒ anche g: Y → Z è una funzione invertibile, con inversa g⁻¹: Z → Y, allora la funzione composta h = g ∘ ƒ: X → Z definita da z = h(x) = g(ƒ(x)) è pure invertibile, e risulta h⁻¹ = ƒ⁻¹ ∘ g⁻¹, cioè x = ƒ⁻¹ (g⁻¹(z)). Si noti che la funzione composta ƒ⁻¹(ƒ(x)) = x è la funzione identità in X, mentre ƒ(ƒ⁻¹(y)) = y è la funzione identità in Y.

Un caso particolarmente importante è quello in cui X e Y sono sottoinsiemi di R. Le due equazioni y = ƒ(x) e x = ƒ⁻¹(y) ammettono le stesse soluzioni, e dunque la stessa rappresentazione grafica nel piano cartesiano R²; tuttavia, se si vuole utilizzare l’asse delle ascisse per rappresentare la variabile indipendente e quello delle ordinate per la variabile dipendente, la funzione inversa di ƒ deve essere scritta nella forma y = g(x) (con g = ƒ⁻¹) e il suo grafico si ottiene da quello di y = ƒ(x) con la simmetria di asse la bisettrice del primo e terzo quadrante.

Si noti che le funzioni e le loro inverse sono leggi di corrispondenza e in quanto tali sono indipendenti dalle lettere che si utilizzano per rappresentarle. Nei casi più comuni la funzione inversa assume un nome e un simbolo particolare, per evitare la notazione ƒ⁻¹ che potrebbe essere confusa con la notazione del reciproco della funzione (il reciproco deve invece essere indicato con (ƒ(x))⁻¹ oppure con 1/ƒ(x)). Per esempio, data la funzione esponenziale y = e^x, risulta X = R, Y = R⁺; la funzione inversa, che è la funzione logaritmo, x = lny, è definita in R⁺ e ha come codominio R. Risulta inoltre ln(e^x) = x, ∀x ∈ R, mentre e^lny = y, ∀y ∈ R⁺.

Una condizione sufficiente per l’invertibilità di funzioni ƒ: R → R è la loro stretta monotonia: se ƒ è strettamente crescente (o decrescente), infatti, è garantita l’iniettività della corrispondenza. Tale ipotesi non è di per sé necessaria, come mostra l’esempio della funzione così definita per casi:

La funzione ƒ così definita non è monotòna in nessun intervallo, tuttavia è invertibile, e ƒ⁻¹ = ƒ. Anche la funzione y = 1/x, con X = Y = R{0} (cioè di dominio e codominio l’insieme dei reali con esclusione di 0, a volte indicato anche con R₀) è invertibile pur senza essere globalmente monotòna, anche se lo sono le sue restrizioni a R⁻ e R⁺.

Se tuttavia ci si restringe allo studio di funzioni continue in un intervallo, la stretta monotonia diviene anche condizione necessaria per la biunivocità della corrispondenza. La funzione inversa è allora anch’essa continua e strettamente monotòna. Nel caso di funzioni continue non monotòne, la invertibilità si può ottenere solo mediante una opportuna restrizione del dominio della funzione. Per esempio, la funzione y = x ² non è monotòna su tutto R, e quindi non è invertibile. Lo è invece se si restringe il dominio a [0, +∞), nel qual caso la funzione inversa è x = √(y).

Anche in (‒∞, 0] è possibile invertire la funzione, ottenendo x = − √(y).

Il caso in cui ƒ non è iniettiva dà luogo a una relazione inversa, che prende il nome di funzione solo in casi particolari (→ funzione polidroma).