funzione booleana

funzione booleana

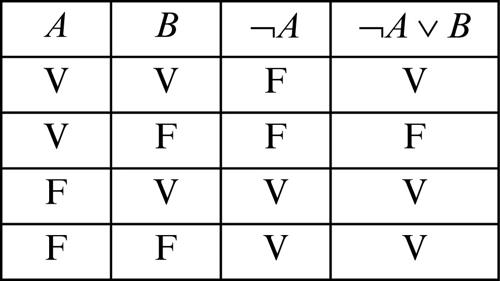
funzione booleana funzione binaria a variabili binarie. È una funzione che è applicata a un insieme di variabili binarie che assumono ciascuna uno di due possibili valori, per esempio i valori 0 e 1, e dà come risultato 0 o 1. Per esempio, se x e y sono variabili binarie che possono assumere solo i valori 0 e 1, allora la funzione binaria definita da ƒ(x, y) = x ⋅ y è una funzione booleana i cui valori sono ƒ(0, 0) = 0, ƒ(0, 1) = 0 , ƒ(1, 0) = 0, ƒ(1, 1) = 1. Al contrario, la funzione definita da g(x, y) = x + y non è una funzione booleana perché applicando tale funzione alla coppia di valori (1, 1) si ottiene un valore diverso da 1 o 0. Le varie operazioni definite nell’algebra di → Boole (prodotto logico, somma logica, complemento...) sono esempi di funzioni booleane. Interpretando i valori 0 e 1 come valori di verità, rispettivamente «falso» e «vero», si può affermare che ogni tavola di verità genera una funzione booleana. A titolo di esempio è riportata la tavola di verità relativa all’enunciato ￢A ∨ B

A questa tavola di verità è associata la funzione booleana ƒ(x, y) che assume i seguenti valori: ƒ(1, 1) = 1, ƒ(1, 0) = 0, ƒ(0, 1) = 1, ƒ(0, 0) = 1.