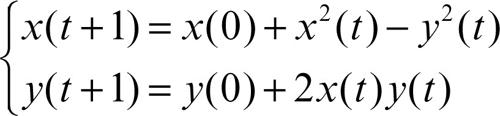frattale

frattale

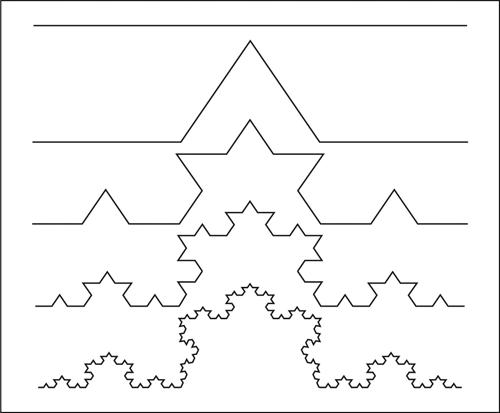
frattale termine con cui si indicano oggetti geometrici (in particolare curve) dotati di alcune caratteristiche peculiari come l’autosomiglianza o autosimilarità e la dimensione frazionaria (da cui deriva il termine frattale, anche se a rigore sarebbe più corretto parlare di «dimensione reale») (→ dimensione frattale). Per autosomiglianza si intende la proprietà di una figura di poter essere suddivisa in più parti identiche all’originale, ma di dimensioni ridotte. Si tratta di una proprietà comune anche a figure non frattali (per esempio, un quadrato può essere scomposto in quattro quadrati più piccoli), ma la differenza tra le figure della tradizione geometrica euclidea (poligoni, cerchi ecc.) e i frattali sta nella dimensione, che per i frattali non è rappresentata da un numero naturale, bensì da un numero reale non negativo. Per esempio, uno dei frattali più famosi, noto come isola di Koch (studiata per la prima volta da Helge von Koch nel 1904), si ottiene come limite di una successione di curve, partendo da un triangolo equilatero: a ogni passo, ciascuno dei lati viene diviso in tre parti uguali; le parti centrali vengono rimosse e sostituite ognuna con i due lati che con esse formerebbero altri triangoli equilateri, rivolti verso l’esterno e più piccoli. In questo modo, se il passo 0 è quello del triangolo equilatero di lato /, al passo 1 si ottiene una stella a sei punte; al generico passo n la curva avrà 3 ⋅ 4ⁿ lati di lunghezza (1/3ⁿ) ⋅ l. La curva che si ottiene al tendere di n a + ∞ ha una lunghezza infinita ma delimita un’area finita (si può dimostrare che è 1,6 volte l’area del triangolo di partenza) ed è una curva frattale. La linea ha la proprietà di non essere derivabile in nessun punto e di essere autosomigliante; infatti, dallo stesso procedimento con cui la curva è realizzata risulta che ogni lato contiene 4 copie identiche di sé stesso, di lunghezza pari a 1/3 dell’originale. Per una figura autosomigliante, alla dimensione D può essere applicata la relazione

dove N è il numero di figure identiche all’originale ottenute da una scomposizione della figura e r il rapporto di riduzione delle dimensioni lineari delle figure più piccole rispetto all’originale. Per l’esempio già fatto del quadrato, se si sceglie N = 4 si ottiene r = 2 e quindi D = 2. Per un cubo, con N = 8 si avrebbe r = 2 e quindi D = 3. Per la curva di Koch, N = 4, ma r = 3 da cui si ricava D = (log N)/(log r) = 1,2681..., per cui non si ottiene come dimensione un numero intero, ma un numero reale. Risulta quindi una dimensione intermedia tra quella di una linea e quella di una superficie.

A differenza delle figure dell’ordinaria geometria, un frattale non può essere definito da un’equazione, ma da una procedura iterativa che può essere ripetuta infinite volte. I frattali come l’isola di Koch che sono generati mediante algoritmi iterativi sono detti frattali per iterazione di funzioni o frattali deterministici; altri frattali di questo tipo sono la polvere di → Cantor e la spugna di → Sierpiński, costruita anche in versione triangolare (triangolo di Sierpiński). I frattali non deterministici sono detti frattali aleatori.

Un altro tipo di figure frattali ha invece a che fare con lo studio dei → sistemi dinamici non lineari; infatti le regioni di convergenza di un sistema dinamico possono avere caratteristiche tali da poter essere definite frattali. Il più famoso di questi frattali è l’insieme di → Mandelbrot (dal nome del matematico francese cui si deve la formalizzazione della teoria dei frattali), che è la regione di convergenza del sistema dinamico del secondo ordine descritto dalle equazioni:

Tale sistema dinamico può essere scritto in forma più semplice ricorrendo alla notazione in numeri complessi: indicando con z il numero complesso x + iy, la legge dinamica del sistema si può esprimere nella forma: z(t + 1) = z(0) + z ²(t). Modificando la legge dinamica dell’insieme di Mandelbrot come: z(t + 1) = c + z ²(t), dove c è una costante complessa arbitraria, si ottengono gli insiemi di → Julia, il cui aspetto varia a seconda del valore di c scelto.

Per gli sviluppi di questo settore della matematica e le applicazioni dello studio dei frattali si veda → geometria frattale.