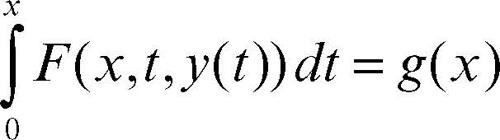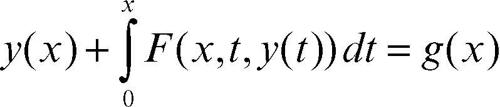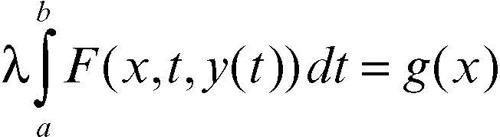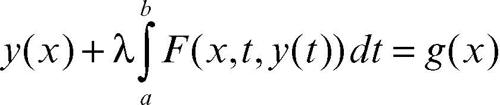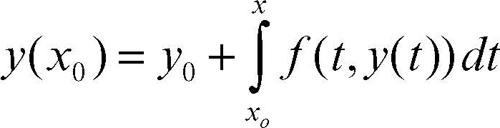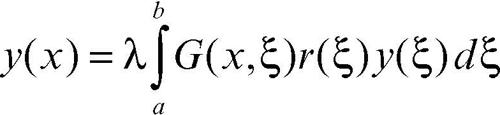equazione integrale

equazione integrale

equazione integrale equazione in cui l’incognita y(x) è una funzione che compare sotto un segno di integrazione. Le equazioni integrali si dicono di prima specie se l’incognita compare solo sotto l’integrale, di seconda specie se compaiono anche al di fuori di tale segno. Si distinguono poi le equazioni integrali in equazioni di → Volterra, se un estremo dell’integrale è variabile, ed equazioni di → Fredholm se gli estremi dell’integrale sono fissi. Si hanno pertanto i quattro tipi seguenti:

• Volterra, I specie:

• Volterra, II specie:

• Fredholm, I specie:

• Fredholm, II specie:

Nel caso lineare la funzione F ha la forma F(x, t, y) = K(x, t)y, dove la funzione K si dice nucleo.

Alle equazioni di seconda specie si perviene in particolare considerando i problemi di → Cauchy e i problemi ai limiti per un’equazione differenziale ordinaria (→ equazione differenziale, problemi ai limiti per una). Infatti integrando l’equazione y′ = ƒ(x, y), per il problema di → Cauchy y(x0) = y0 si ottiene

che è una equazione integrale di Volterra. Analogamente un problema ai limiti omogeneo nell’intervallo [a, b] per l’equazione lineare (p(x)y′ )′ − q(x)y + λr(x)y = 0 si trasforma, mediante le identità di → Lagrange, nell’equazione integrale di Fredholm

dove G è la funzione di → Green, associata al problema. Le equazioni integrali di Volterra, sotto opportune ipotesi (per esempio, una condizione di → Lipschitz del nucleo rispetto all’incognita y) hanno una e una sola soluzione. Per quelle di Fredholm (nel caso lineare) invece si ha la possibilità di autovalori, per i quali l’equazione omogenea può ammettere infinite autosoluzioni.