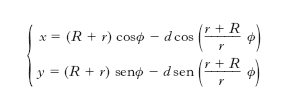epiciclo
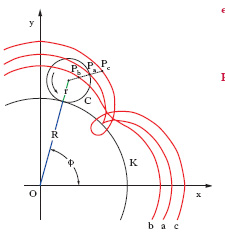
Curva piana o sferica, che rotola senza strisciare su un’altra curva (anch’essa piana o sferica) fissa. È particolarmente importante il caso di e. circolare: quando la curva fissa è una retta, i punti rigidamente collegati all’e. descrivono una cicloide, mentre quando la curva fissa è una circonferenza, descrivono un’epicicloide o un’ipocicloide a seconda che la tangenza sia esterna o interna. Ruote dentate a profili cicloidali hanno origine da e. rotolanti sulle primitive (➔ ruota). Curva epicicloide Curva piana descritta da un punto P rigidamente collegato a un cerchio C (epiciclo) che rotoli senza strisciare sopra un cerchio fisso K del suo piano e sia tangente esternamente a K. Una epicicloide si dice ordinaria, accorciata o allungata, secondo che P sia su C (Pa in fig.), interno a C (Pb), esterno a C (Pc). Indicando con R il raggio del cerchio K, con r il raggio del cerchio C, con d la distanza di P dal centro di C, si ottengono per la epicicloide (con opportuna scelta degli assi x e y) le seguenti equazioni parametriche:
ove ϕ è l’angolo indicato in fig. Esistono strumenti per il tracciamento delle epicicloidi. Una epicicloide è una curva algebrica chiusa quando il rapporto tra il raggio di C e quello di K è razionale: in fig. è illustrato il caso in cui tale rapporto è 1 : 4. Se, invece, esso è un numero irrazionale l’epicicloide non risulta chiusa ed è una curva trascendente.