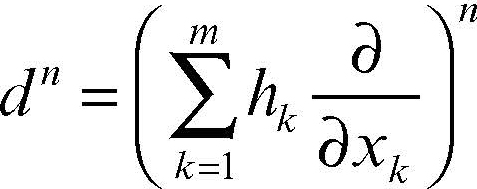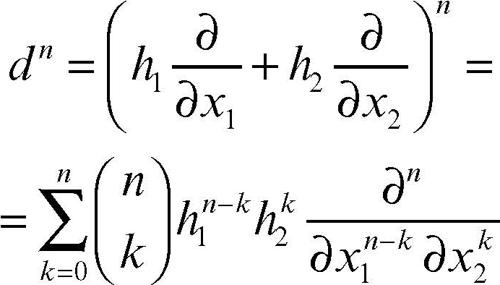differenziazione

Enciclopedia della Matematica (2013)

differenziazione


differenziazione operazione che a una funzione associa il suo → differenziale. Per una funzione di m variabili, l’operatore di differenziazione è dato da

formula

dove gli hk sono incrementi nella varabile xk. Le potenze di questo polinomio formale danno i differenziali successivi:

formula

Se le variabili indipendenti sono due, per esempio, si tratta della potenza di un binomio, e

formula

Quindi dnƒ è un polinomio omogeneo di grado n negli incrementi h1 e h2, i cui coefficienti sono dati dalle derivate parziali n-esime di ƒ moltiplicate per i coefficienti binomiali. Per m > 2 variabili indipendenti si usa la formula della potenza del multinomio (→ teorema multinomiale).

Vedi anche
anàlisi infinitesimale (o càlcolo) Parte della matematica (detta anche semplicemente analisi matematica) i cui metodi e sviluppi sono fondati sull'operazione di passaggio al limite. Suoi iniziatori sono considerati nel 17° sec. I. Newton e G.W. Leibniz, tuttavia ha avuto il suo sviluppo solo in seguito alla definizione rigorosa ... Karl Theodor Wilhelm Weierstrass Matematico (Osterfeld, Münster, 1815 - Berlino 1897). Prof. all'univ. di Berlino, membro dell'Accademia di Berlino,  fu celebrato dai matematici contemporanei come il più grande analista vivente. Portano il suo nome molti teoremi sia nell'analisi infinitesimale, sia nella teoria delle funzioni. Vita ... approssimazione In matematica, si chiamano metodi, o procedimenti di a. o, semplicemente, a., procedure alle quali si ricorre per rappresentare enti matematici (numeri, misure, funzioni ecc.) in modo non esatto, ma sufficientemente accurato per gli scopi perseguiti, in genere mediante enti più semplici. Così, per es., ... David Hilbert {{{1}}} Matematico tedesco (Königsberg 1862 - Gottinga 1943). È la figura più notevole della matematica della prima metà del Novecento e forse dell'intero secolo. A Königsberg frequentò l'università con A. Hurwitz, già professore, e con H. Minkowski, suo condiscepolo. Dal 1895 al 1929 fu prof. all'univ. ...
Tag
Altri risultati per differenziazione
  • derivata
    Dizionario di Economia e Finanza (2012)
    Concetto fondamentale in analisi matematica, ampiamente utilizzato nelle applicazioni economiche. Per dare un’idea della potenza di questo strumento nella teoria economica, si pensi, per es., che la d. del ricavo (costo) totale è il ricavo (costo) marginale e la massimizzazione del profitto (differenza ...
  • derivata
    Enciclopedia on line
    Concetto fondamentale nell’analisi matematica e nelle sue applicazioni che esprime, date due grandezze l’una funzione dell’altra (per es., in fisica, lo spazio percorso e il tempo impiegato a percorrerlo, o anche, in economia, il prodotto ottenuto al variare della quantità di fattori di produzione impiegati ...
  • derivata
    Dizionario delle Scienze Fisiche (1996)
    derivata [s.f. dall'agg. derivato] [ANM] Il risultato dell'operazione di derivazione: nella sua forma più semplice, cioè nel caso in cui f(x) sia una funzione reale di una variabile reale x, la d. di f(x) in un punto x₀, che si denota con f'(x₀) o Df(x₀) o df(x₀)/dx, è, per definizione, il limite del ...
  • DERIVATA
    Enciclopedia Italiana (1931)
    Termine matematico, rispondente a un concetto, che trova applicazione nello studio d'ogni legge di mutua dipendenza tra grandezze geometriche o meccaniche o fisiche, ecc. Siano x ed y le misure di due grandezze variabili, tali che, in forza d'una legge qualsiasi, la y dipenda dalla x o, come si dice ...
Vocabolario
de-differenziazione
de-differenziazione s. f. In biologia, il processo tramite cui una cellula specializzata viene ricondotta allo stato di cellula staminale. ◆ «La clonazione è il modo più semplice per ottenere la de-differenziazione, cioè il ritorno dallo...
differenziazióne
differenziazione differenziazióne s. f. [der. di differenziare]. – 1. L’atto, il fatto di differenziare, cioè di rendere differente o di trattare in modo differente; il processo per cui si diviene differente, si acquistano cioè caratteri...