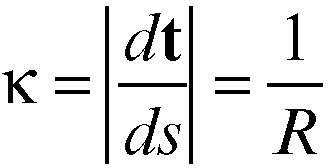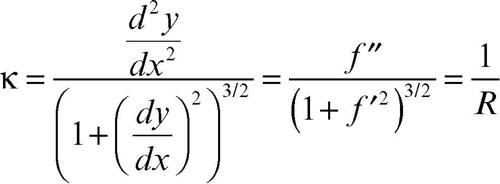curvatura

curvatura

curvatura o flessione, numero che misura la rapidità dello scostamento di una curva dall’andamento rettilineo in prossimità di un suo punto. Se la curva è rappresentata parametricamente mediante l’ascissa curvilinea, x = ψ(s), la curvatura κ in un punto x₀ = ψ(s₀), è data dalla norma della derivata del versore tangente, t = d ψ/ds

per s = s₀. La curvatura è anche indicata con la lettera latina C.

Curvatura di curve piane

Se la curva è una curva piana regolare ed è assegnata in forma cartesiana esplicita y = ƒ(x), la sua curvatura è data da

Se la curvatura è nulla in un punto si dice che la curva ha un flesso nel punto stesso. Se la curvatura è identicamente nulla la curva è una retta. Se la curvatura non è nulla, il suo reciproco, R, è detto raggio di curvatura.

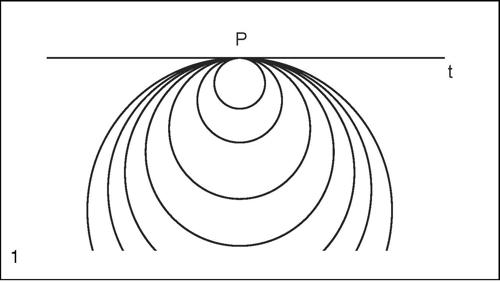
In una circonferenza di raggio r la curvatura è costante in ogni punto ed è pari a 1/r; quindi, maggiore è il raggio di una circonferenza, minore risulta la sua curvatura, che al limite vale zero per una retta.

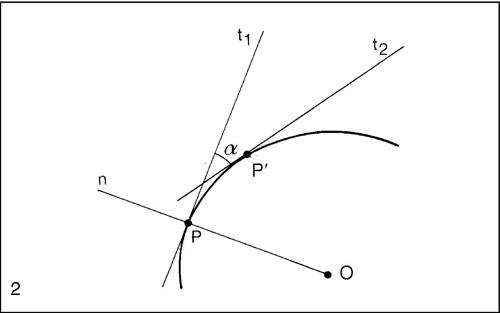
Il punto O = x₀ + Rn della curva (dove n indica il versore normale alla curva) è detto centro di curvatura; il cerchio con centro in tale punto e raggio R è detto cerchio osculatore.

Curvatura di curve sghembe

Per una curva sghemba si possono definire due diverse curvatura dette, rispettivamente, flessione (o prima curvatura) e torsione (o seconda curvatura). La flessione misura, localmente, quanto la curva si discosta dall’andamento rettilineo, la torsione misura, localmente, quanto la curva si discosta dall’essere piana.

Curvatura di una superficie

Curvature principali di una superficie in un suo punto sono il minimo e il massimo valore (presi con segno opportuno) che può assumere la curvatura delle curve tracciate sulla superficie passanti per il punto le cui normali principali abbiano la stessa direzione della normale alla superficie nel punto stesso: la loro somma è la curvatura media e il loro prodotto è la curvatura totale della superficie nel punto. Il → Theorema Egregium di Gauss afferma che, sotto opportune ipotesi di derivabilità, la curvatura totale di una superficie resta invariata in ogni punto, comunque si deformi rigidamente la superficie stessa.