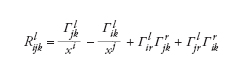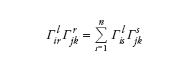curvatura scalare
curvatura scalare
Sia Mν una varietà riemanniana regolare, ovvero una varietà C∞ sulla quale è specificato un campo tensoriale definito positivo g(x) (x indica qui un sistema di coordinate locali), detto tensore metrico o metrica. Sia inoltre TMν lo spazio dei campi vettoriali regolari tangenti a Mν. La curvatura su Mν è normalmente caratterizzata in termini del tensore di (curvatura di) Riemann, un’applicazione multilineare R:TMν×TMν× ×TMν→TMν definita dalla formula
R(X,Y)Z = ∇Χ∇ϒ Z − ∇ϒ ∇Χ Z − ∇[Χ,ϒ] Z
dove X,Y,Z∈TMν, ∇ indica la derivata covariante (o connessione di Levi-Civita) su Mν e [∙,∙] il prodotto di Lie. La derivata covariante è strettamente connessa con la nozione di trasporto parallelo di un vettore in TMνπ, lo spazio tangente a Mν in p, e la quantità R(X,Y)Z (calcolata in uno specifico punto p) può essere considerata una misura della variazione subita dal vettore Z dopo uno spostamento parallelo lungo i lati di un rettangolo infinitesimo con lati a due a due paralleli alle direzioni determinate dai vettori X(p) e Y(p). Tale variazione nel caso di un piano nello spazio euclideo tridimensionale (in realtà n-dimensionale) è nulla: il piano è ‘piatto’. Scegliendo un sistema di coordinate locali x, i coefficienti del tensore di Riemann possono essere espressi nella forma
dove Γιξκ sono i simboli di Christoffel e
(contrazione degli indici). La curvatura scalare è allora definita dalla formula R=gικRλιλκ. Si può notare che tutti gli indici sono contratti e dunque si tratta effettivamente di un numero reale (scalare). Se la curvatura scalare in un punto p di Mν è positiva il volume di una palla infinitesima è minore di quello di una palla nello spazio euclideo n-dimensionale, viceversa se è negativa. Nel caso di una superficie bidimensionale, la curvatura scalare è esattamente il doppio della curvatura di Gauss.
→ Analisi non lineare: metodi variazionali