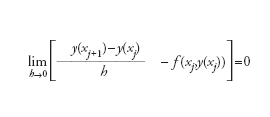consistenza
consistenza
Si consideri il problema di trovare u tale che F(u,d)=0, dove d è l’insieme dei dati da cui dipende la soluzione e F esprime la relazione (detta anche legge funzionale) che lega u a d. Supponendo che il modello matematico F(u,d)=0 sia ben posto, ovvero che esista un’unica soluzione u e questa dipenda con continuità dai dati d, risolverlo in maniera approssimata con un metodo numerico significa costruire una successione di problemi approssimati Fν(uν,dν)=0, con n≥1. Il parametro n è un indice del livello di difficoltà del problema approssimato (spesso è legato alla sua dimensione, ovvero al numero di gradi di libertà necessari a determinarne la soluzione). Se il dato d del problema F(u,d)=0 è ammissibile per Fν, diremo che il metodo numerico Fν(uν,dν)=0 è consistente se Fν(u,d)=Fν(u,d)−F(u,d)→0 per n→∞, ovvero se il modello numerico Fν traduce correttamente la legge funzionale F. A titolo di esempio, consideriamo il seguente modello matematico: trovare la funzione y(x) soluzione del problema di Cauchy y′(x)=f(x,y(x)) per x∈(x0,b) con condizione iniziale y(x0)=y0, dove la funzione f e il dato y0 sono assegnati. Un possibile modello numerico per la risoluzione del problema di Cauchy è dato dal metodo di Euler in avanti. Assegnato un parametro h>0 e definiti i nodi xj=x0+j∙h (per j=0,…,n e n=[(b−x0)/h]), il metodo di Euler approssima la soluzione y(x) nei nodi xj secondo la formula vj+1=vj+hf(xjvj) (per j=0,…,n−1), con v0=y0. Verificare che il metodo di Euler è consistente equivale a verificare che limν→∞ Fν(u,d)=0, ovvero che
per ogni j=0,…,n. Tale uguaglianza è chiaramente verificata dalla funzione y(x) soluzione del problema di Cauchy assegnato, in quanto essa verifica f(xj,y(xj))=y′(xj).