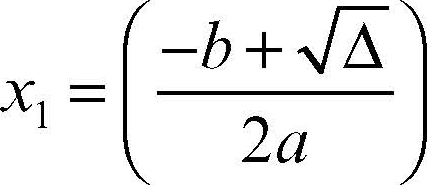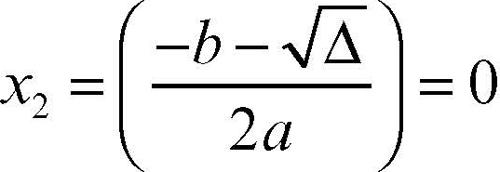cancellazione numerica

cancellazione numerica

cancellazione numerica errore algoritmico che si ottiene quando operando con un automa esecutore, per esempio un computer, si addizionano due numeri di segno opposto con valore assoluto quasi uguale. A causa dell’aritmetica finita con cui opera l’automa (genericamente indicato come “macchina”) può verificarsi che si ottenga come risultato 0 anche se i due addendi non sono numeri opposti. Quando ciò si verifica, ogni calcolo successivo rischia di non avere alcun significato, date le proprietà particolari di 0. Per esempio, se in un’equazione di secondo grado

si ha che

nel senso che il valore assoluto della differenza

è minore della precisione della macchina, allora è necessario che una soluzione si trovi con la formula standard

mentre l’altra, che avrebbe valore nullo applicando la formula

va calcolata a partire dalla relazione x₁x₂ = c/a da cui x₂ = c/ax_1. Con un diverso algoritmo di calcolo è perciò possibile ridurre l’errore, fino talvolta a eliminarlo.

Le regole operative che valgono all’interno dell’ambiente di calcolo degli elaboratori elettronici, o computer, possono essere diverse dalle usuali regole algebriche, a causa degli errori generati durante le procedure automatizzate. In particolare, se x′ + y′ è la somma esatta di due numeri appartenenti all’insieme dei numeri macchina, essa è in generale diversa dalla somma calcolata dalla macchina stessa (x′ + y′ )′. Per esempio, se una macchina rappresenta i numeri in forma esponenziale con 4 posti per le cifre e 1 posto per l’esponente di 10 e x′ = 1.234E + 3 e y′ = 5.678E − 1, la loro somma esatta è x′ + y′ = 1.2345678E + 3, ma la somma calcolata dalla macchina è (x′ + y′ )′ = 1.235E + 3, dovendo effettuare l’arrotondamento alla quarta cifra significativa. Quindi risulta x′ + y′ ≠ (x′ + y′ )′.

Il calcolo della somma di due numeri è tra i più semplici algoritmi che si possano far eseguire a un automa, ma la diversità di comportamento dell’algebra interna della macchina rispetto alle regole aritmetiche compare in molte e diverse situazioni: nell’elaborazione dei dati, nel calcolo del valore di una formula, nella determinazione delle soluzioni di un’equazione, nell’esecuzione di metodi iterativi, nei quali gli errori di approssimazione determinati dalla ripetizione delle operazioni possono propagarsi sino a rendere del tutto insignificanti i risultati ottenuti.