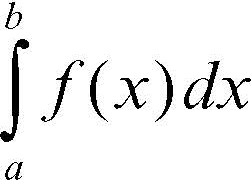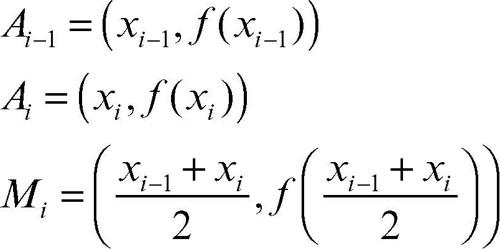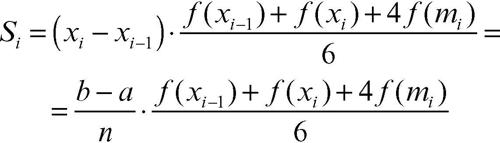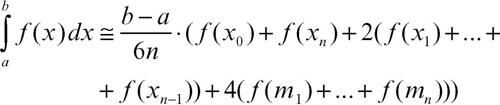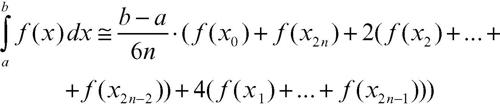Cavalieri-Simpson, approssimazione di

Cavalieri-Simpson, approssimazione di

Cavalieri-Simpson, approssimazione di fornisce la formula finale del metodo di Cavalieri-Simpson, utilizzata per calcolare numericamente l’integrale definito

di una funzione y = ƒ (x) continua in un intervallo [a, b] ⊂ R. Tale approssimazione si ottiene suddividendo l’intervallo di integrazione [a, b] in sottointervalli uguali e approssimando l’andamento della funzione in ciascun sottointervallo con opportuni segmenti parabolici. Il risultato finale si ottiene sommando le aree che ciascun segmento parabolico forma con l’asse delle ascisse.

Si consideri dunque una suddivisione di [a, b] in un numero n pari di sottointervalli uguali [x_i−1, x_i] per i = 1, 2, …, n approssimando in ciascuno di essi la funzione ƒ con una parabola passante per i seguenti tre punti:

dove M_i rappresenta il punto appartenente al grafico della funzione ƒ in corrispondenza dell’ascissa media

del sottointervallo [x_i−1, x_i]. Con semplici calcoli si può trovare l’area del singolo segmento parabolico in funzione delle ascisse di A_i−1, A_i, M_i:

I sottointervalli [x_i−1, x_i] sono uguali e ripartiscono l’intervallo [a, b]; poiché il calcolo dell’area del segmento parabolico è invariante per traslazione, si ottiene facilmente la formula di approssimazione di Cavalieri-Simpson:

Di questa formula viene data spesso un’espressione algoritmica più efficace, considerando anche i valori medi degli intervalli come valori di x, indicati da uno stesso indice; così, al posto di x₀, m₀, x₁, si indica x₀, x₁, x₂. In tal modo i valori estremi degli intervalli risultano quelli di indice pari e i valori medi quelli di indice dispari. La formula diventa allora:

Il metodo generale di approssimazione così formalizzato prende il nome di metodo di Cavalieri-Simpson. Poiché tali parabole risultano, a seconda dei casi, con concavità rivolta verso l’alto o verso il basso, il metodo approssima bene il grafico di una funzione che abbia la derivata seconda di segno non costante. Come in ogni metodo approssimato si può dare una stima dell’errore commesso, così anche in questo caso è possibile fornire una maggiorazione dell’errore assoluto. Si può dimostrare che se la funzione integranda è derivabile quattro volte nell’intervallo considerato e se |ƒ IV(x)| ≤ M, allora l’errore assoluto e_a che si commette si può così stimare:

dove h indica il passo di integrazione, cioè l’ampiezza di ciascun sottointervallo. Poiché la valutazione analitica dell’errore non è semplice, si preferisce ricorrere a metodi empirici, il più noto dei quali è il cosiddetto metodo del dimezzamento del passo: dopo aver ottenuto un’approssimazione I₁ dell’integrale, si calcola un’ulteriore approssimazione I₂, dimezzando il passo di integrazione da h a h/2. Si dimostra che l’errore assoluto del metodo, e_a, è maggiorato dalla quantità

ossia