trattrice
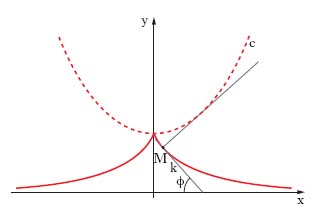
trattrice (o t. della retta) In matematica, la curva piana caratterizzata dal fatto che il segmento di tangente compreso tra il punto di contatto M e una retta fissa è costante (v. fig.). Se k è la misura del segmento e l’asse x è la retta data, si hanno le equazioni parametriche x=k logtg(ϕ/2)+k cosϕ, y=k senϕ, nelle quali il parametro ϕ è l’angolo della tangente variabile con l’asse x. Integrando l’equazione differenziale y2+(y/y′)2=k2 si ha l’equazione cartesiana della t.: x = k settcosh (k / y) ± √‾‾‾‾‾‾‾ k2−y2. La t. non è perciò una curva algebrica; tuttavia i punti di contatto delle tangenti condotte a essa da un punto qualunque del piano appartengono a una curva algebrica del quart’ordine. Un’altra proprietà della t. è di essere un’evolvente della catenaria (c in fig.). La t. ammette l’asse x come asintoto; facendola ruotare attorno a esso si ottiene la pseudosfera di Beltrami. La t. rientra tra le curve di inseguimento.