Guldino, teoremi di
Guldino, teoremi di
Guldino, teoremi di o teoremi di Pappo-Guldino, teoremi di geometria che si riferiscono a una figura di rotazione. Essi devono il nome al matematico P. Guldino, che elaborò e dimostrò un’intuizione già avuta dal matematico greco Pappo (da cui il doppio nome con cui spesso i teoremi sono riportati) vissuto alla fine del iii secolo d.C. e appartenente alla cosiddetta Scuola alessandrina. I teoremi permettono di calcolare l’area e il volume dei solidi di rotazione.
Una figura piana F che ruota attorno a una retta a giacente nel suo stesso piano genera un solido di rotazione E e il suo contorno ∂F genera la superficie ∂E. Si hanno allora i due risultati:
• il volume di E si ottiene moltiplicando l’area della figura ruotante F per la lunghezza della circonferenza descritta dal baricentro di F;
• l’area di ∂E si ottiene moltiplicando la lunghezza di ∂F per la lunghezza della circonferenza descritta dal baricentro di ∂F.
Se la retta a interseca F, i valori ottenuti sono la differenza rispettivamente dei volumi e delle aree descritti dalle due porzioni di F che si trovano nei due semipiani di origine a.
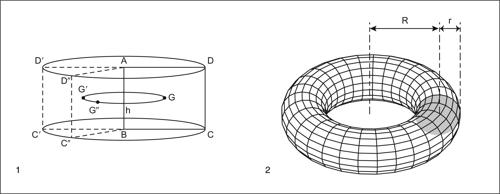
Per esempio, se un rettangolo ABCD di base r e altezza h ruota attorno al lato h genera un cilindro il cui volume πr 2h è uguale al prodotto dell’area rh del rettangolo per la lunghezza 2π(r /2) = πr descritta dal suo baricentro G. La superficie del cilindro ha area 2(r + h) ⋅ πr = 2πr 2 + 2πrh, somma delle aree delle basi e di quella laterale.
Se si fa ruotare un cerchio di raggio r attorno a una retta che dista R > r dal suo centro si ottiene un toro, il cui volume vale πr 2 ⋅2πR = 2π2r 2R e la cui superficie ha area 4π2rR.
I teoremi possono essere utilizzati anche per calcolare il baricentro di una figura piana: per esempio, se si fa ruotare un semicerchio di raggio r attorno al suo diametro si ottiene una sfera e dall’uguaglianza
essendo x̄ il raggio della circonferenza descritta dal baricentro, si ottiene che il baricentro di un semicerchio dista
dal diametro; analogamente il baricentro della semicirconferenza si trova a
dal diametro.